落石冲击破坏特性试验研究

吴亚华

摘 要：针对落石碰撞地面后解体这一现象，对落石解体全过程进行了全面而详细的论述。由应力波的传播速度与荷载加载速度得出裂纹扩展方向为从底部至顶部的结论，从应力角度对已有冲击力计算经验公式进行了分析，提出了一种冲击力计算公式，并推出了临界破裂高度，从能量角度建立了可用于定量计算的落石解体能量方程，并通过实验对上述理论进行了验证。结果表明，在垂直于加载方向上，拉应力超过抗拉强度时落石解体，解体后的运动方式可由落石解体能量方程给出。

关键词：解体 冲击力 能量守恒 落石

中图分类号：TU451 文献标识码：A 文章编号：1674-098X（2017）02（a）-0039-05

Abstract： In reaction to the phenomenon that rockfall disintegrates after the collision with the ground， we expound the whole process of rockfalls disintegration comprehensively and detailedly. Across the spread speed of the stress wave and the loading speed， we conclud that the direction of crack growth arise from the bottom to the top. Across the stress， we analyze the empirical equation of impact force and put forward a new computational formula. Then the rupture height is launched. Considering the energy， we establish an energy equation of rockfalls disintegration for quantitative calculation and verify this theory across an experiment. The result indicates that the rockfall breaks up when the tensile stress exceeds the tensile strength in the direction perpendicular to the load. The energy equation gives out the movement way after the disintegration.

Key Words： Disintegration； Impact force； Conservation of energy； Rockfall

危岩崩塌是次生型地质灾害，落石是其中最常见的灾害。Olsson R分析了冲击力与土层之间的关系式[1]；Corò D等对阿尔卑斯山地区崩塌落石的时空特性进行了分析[2]；Atkinson C等研究了巴西圆盘开裂试验，建立了能量释放率计算公式，建立了能量释放率与应力强度因子相对应的计算公式[3]；Ramulu M 等对玄武岩破裂进行了研究，得到了其循环爆破冲击的关系式[4]；Daudon D等将离散元数值模型构建技术用于分析岩石解体，结果表明，岩石解体能量耗散与颗粒形状以及边坡几何特征对有很大关系[5]；Kirkby M J和Statham I建立了岩石路径计算模型[6]；郭绍平等对冲击力的计算方法进行了详细分析并进行了创新改进[7]；袁进科等进行了一系列试验，研究了和落石接触的各种地面因素对落石最大冲击力的影响[8]；金解放等为了研究岩石损伤累积演化特征，进行了动静组合荷载的试验，提出了在这种情况下的数学模型[9]；苏承东等为了研究局部剪切失稳破坏和全面剪胀失稳破坏之间的关系，对岩石进行了压缩试验，结果表明，岩石的锥形破坏常发生在高应变速率下[10]；左建平等建立了脆性岩石能量跌落系数，研究了循环加载、循环卸载，得到了输入能、耗散能、机械能、弹性应变能、塑性应变能等在岩石变形破坏全过程的具体情况[11]；宋义敏等研究了局部化带的演化，分析了加载过程、卸载过程、能量积累、能量释放等对岩石试件的影响关系[12]；周辉等分析了ωs和ωv在岩石破坏屈服时的变化曲线，分析了危岩破坏屈服机制[13]。该文对落石进行了高处掉落沖击试验，并对研究结果进行了分析解释。

1 宏观过程：裂纹从底部扩展至顶部

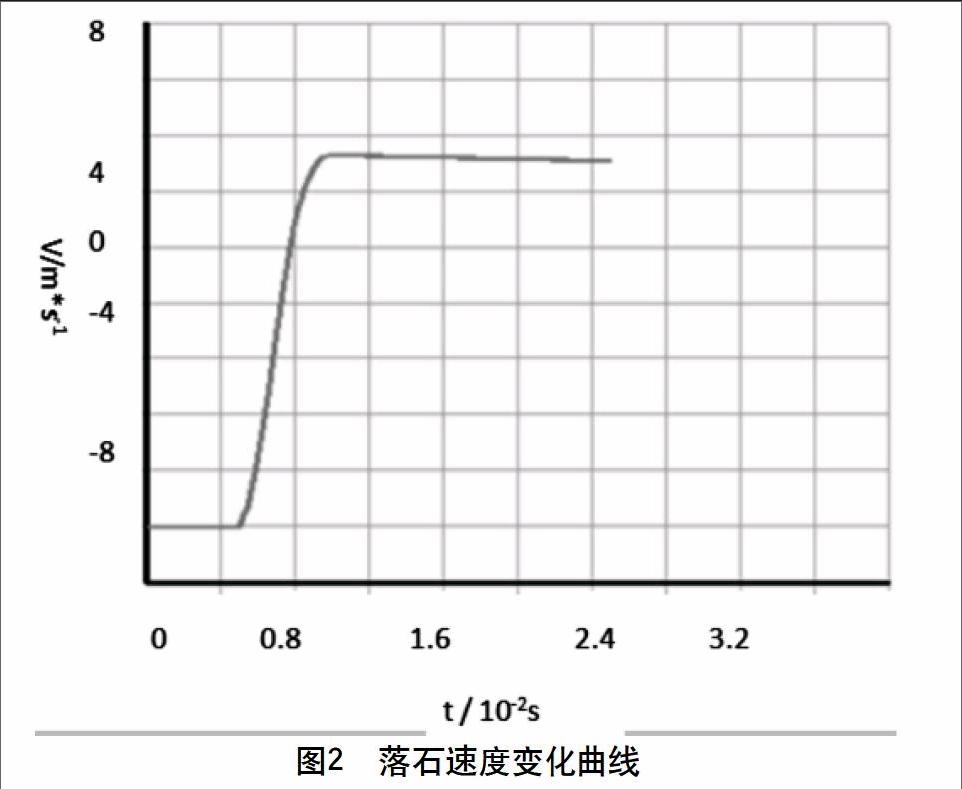
用ansys模拟砂岩落石如图1所示，密 kg/m3，弹性模 N/m2，剪切模 N/m2，泊松，直径1m，碰撞前速度10 m/s，地面为刚性，速度变化结果如图2所示。结果显示，碰撞至压缩量最大时，用时为斜直线的一半，即0.000 25 s，则加载速度4 000 m/s。资料显示[10]，应力波在砂岩中的波速为3 000～4 000 m/s，暂3 000 m/s，从实验室研究得知，裂纹扩展速度一般在纵波速度的1/3以下[11]，暂 m/s，此，与假设的宏观裂纹一致，当碰撞初速度更大时，加载速度更大，仍然符合。由此得到：球形落石冲击地面时，裂纹从底部接触点向上扩展至顶端。

2 试验研

前述假定为：裂纹从落石底部开始扩展至顶部，按此论述，做如下试验，取扁圆形鹅卵石从高处落下，使其鹅卵石边缘和地面碰撞，高度不够时，落石不会破裂，将高度增加，知道落石破裂，观察记录结果。

如图3、图4所示，落石破裂为四块，分别为1、2、3、4，如图5俯视图所示，落石的裂纹为十字形，刚好将鹅卵石对称平分，观察图6裂纹面可以看到，两个裂纹线组成的十字裂纹线，在底端并不是完整的，鹅卵石底部和地面接触区域，形成一个压剪破坏区，可以从图7仰视图中看到，压剪破坏区为菱形。

分析全过程，如图8所示，分为五个阶段。（1）初始碰撞时，鹅卵石和地面接触，应力从零开始增大；（2）鹅卵石继续下落，接触区形成一个椭圆面，在椭圆面上，等应力线呈菱形分布，应力正视图中等应力线为半椭圆形，在椭圆面的四个端点，产生应力集中现象，鹅卵石继续下降，应力集中超过鹅卵石的强度极限，开始产生裂纹；（3）鹅卵石底部椭圆接触面上裂纹迅速扩展贯通，并向鹅卵石上部扩展，应力正视图中等应力线变为三角形；（4）应力分布的扩展使鹅卵石内部开始破坏，破坏的形状和正视图中等应力线相同，破坏的岩石呈层状堆积在原位置；（5）鹅卵石继续下降，压剪破坏区继续扩大，内部破坏部分彻底碎裂掉落，形成空腔。

3 结语

该文研究了国内外危岩崩塌现状，选取其中落石灾害进行了分析，对落石开裂的方式进行了分析并做了相关试验，初步得到以下结论：

（1）由应力波波速和荷载加载速度，论证了当加载速度足够大时，落石裂缝开裂过程中裂纹是从底部扩展到顶部的结论。

（2）对落石灾害进行了简单试验模拟，观察记录了落石开裂方式，得到了落石冲击的破坏特性。

参考文献

[1] Olsson R.Analytical prediction of large mass impact damage in composite laminates[J].Composites Part A： Applied Science and Manufacturing，2001，32（9）：1207-1215.

[2] Corò D，Galgaro A，Fontana A，et al.A regional rockfall database： the Eastern Alps test site[J].Environmental Earth Sciences，2015，74（2）：1731-1742.

[3] Atkinson C，Ciprian D，Coman，et al.Couple stresses and the fracture of rock[J].Philosophical Transactions of the Royal Society A：Mathematical，Physical and Engineering Sciences，2015，373（2038）：221-235.

[4] Ramulu M，Chakraborty A K，Sitharam T G.Damage assessment of basaltic rock mass due to repeated blasting in a railway tunnelling project-a case study[J].Tunnelling and Underground Space Technology，2009，24（2）：208-221.

[5] Daudon D，Villard P，Richefeu V，et al.Influence of the morphology of slope and blocks on the energy dissipations in a rock avalanche[J].Comptes Rendus Mécanique，2015，343（2）：166-177.

[6] Kirkby M J，Statham I.Surface stone movement and scree formation[J].The Journal of Geology，1975，83（3）：349-362.

[7] 郭紹平，王全才，吴清，等.一种改进的落石冲击力计算方法[J].山地学报，2014，32（3）：345-349.

[8] 袁进科，黄润秋，裴向军.滚石冲击力测试研究[J].岩土力学，2014，35（1）：48-54.

[9] 金解放，李夕兵，邱灿，等.岩石循环冲击损伤演化模型及静载荷对损伤累积的影响[J].岩石力学与工程学报，2014，33（8）：1662-1671.

[10] 苏承东，李怀珍，张盛，等.应变速率对大理岩力学特性影响的试验研究[J].岩石力学与工程学报，2013，32（5）：943-950.

[11] 左建平，黄亚明，熊国军，等.脆性岩石破坏的能量跌落系数研究[J].岩土力学，2014，35（2）：321-327.

[12] 宋义敏，姜耀东，马少鹏，等.岩石变形破坏全过程的变形场和能量演化研究[J].岩土力学，2012，33（5）：1352-1356，1365.

[13] 周辉，李震，杨艳霜，等.岩石统一能量屈服准则[J].岩石力学与工程学报，2013，32（11）：2170-2184.

[14] BrobergKB，著.弹性及弹–塑性介质中的冲击波[M].尹祥础，译.北京：科学出版社，1965：65-79.

[15] 胡刚，郝传波，景海河.爆炸作用下岩石介质应力波传播规律研究[J].煤炭学报，2001，26（3）：270-273.

[16] 黄理兴.动载作用下岩石断裂裂纹的扩展与控制[J].岩土力学，1989，10（1）：53-60.

[17] 余同希，卢国兴.材料与结构的能量吸收[M].北京：化学工业出版社，2006：137.

[18] 章广成，向欣，唐辉明.落石碰撞恢复系数的现场试验与数值计算[J].岩石力学与工程学报，2011，30（6）：1266-1273.

[19] Thornton C.Coefficient of restitution for collinear collisions of elastic-perfectly plastic spheres[J].ASME Journal of Applied Mechanics，1997，64（2）：383-386.

[20] 黎立云，鞠杨，赵占文，等.静动态加载下岩石结构破坏时的能量分析[J].煤炭学报，2009，34（6）：737-740.

[21] 宋小林，谢和平，王启智.大理岩的高应变率动态劈裂实验[J].应用力学学报，2005，22（3）：419-425，508.