火星大气对降落伞充气性能影响的初步探讨

荣伟 包进进



火星大气对降落伞充气性能影响的初步探讨

荣伟 包进进

（北京空间机电研究所，北京100094）

探测火星一直是人类深空探测的热点之一，火星上因存在大气层。降落伞一直是确保火星探测器安全着陆于火星表面的一种重要的气动减速装置。然而，由于火星上大气密度非常稀薄，因此掌握降落伞在火星大气环境下的充气性能是火星探测器着陆系统工程设计中的关键，同时也是火星探测器减速着陆系统工作性能评定的理论分析模型或数值仿真系统中必须要解决的一个问题。文章通过降落伞轴向-径向动量守恒充气模型，研究了大气密度对降落伞充气性能的影响，得到了大气密度对降落伞充气时间、充气距离、充气过程中伞衣面积变化的影响规律。研究结果表明，目前有关降落伞充气性能的一些经验关系式对于火星这种稀薄大气环境已不再适用；在火星稀薄的大气环境下，降落伞的充气时间、充气距离随大气密度的减小将急剧增大；伞衣阻力面积为充气过程中时间的4次多项式关系。该成果对于火星探测器减速着陆系统的工程设计、试验及性能评估等均具有较好的参考价值。

伞衣面积 充气距离 充气时间 降落伞 大气密度 火星大气 深空探测

0 引言

由于火星是距离地球最近的一颗地外行星，它的大气和地表环境比起其它天体来说也更接近于人类居住的条件，因此探测火星一直是人类深空探测的热点之一。自从1960年10月10日前苏联发射第一颗火星探测器以来，火星就成为了人类发射探测器进行或准备进行探测最多的一颗外行星，特别是自20世纪90年代以来，基本上是每两年一次的发射窗口均有火星探测器发射，从未间断。目前我国的火星探测任务也已完成立项，并将于2021年同时实施火星环绕探测和火星表面着陆巡视探测。

由于火星上存在大气层，因此，到目前为止，降落伞始终是确保火星探测器安全着陆于火星表面的一种重要的气动减速装置[1-7]。然而，与地球的相比，火星上大气非常稀薄。火星表面的大气密度约为0.015kg/m3，在离火星表面10km高度处其大气密度约为0.006 5kg/m3，而在离地球表面10km高度处的大气密度约为0.413kg/m3，即火星上的大气密度要比地球的小两个数量级左右。因此，火星上如此稀薄的大气环境对降落伞充气性能的影响如何，是开展火星探测器减速着陆系统设计时必须了解和掌握的，同时也是火星探测器着陆系统工程设计中的关键，是与返回地球上的航天器着陆系统设计的主要不同点之一。

此外，由于地球大气成份与火星上的不同，对于物伞系统在火星大气环境下工作性能的评定，地球上很难通过完全同时模拟其火星环境下的实际工作条件来进行验证，如开伞马赫数和动压在地球上是无法同时模拟的。而是需要通过部分条件的单项模拟试验，再通过理论分析或仿真来综合考虑。然而目前在回收着陆系统工作过程的数值仿真系统中，对于降落伞开伞过程的一些参数，如充气时间、充气距离、伞衣阻力面积的变化，一般是采用经验公式来处理的，而这些充气性能与开伞条件之间的经验关系是通过地球上的一些试验结果统计、拟合出来的[8-9]，且这些关系式中均没有反映出大气密度的影响，同时也很少见到有关大气密度对降落伞充气性能影响的研究。作者曾通过对有关降落伞充气过程的一些常用研究方法的比较分析，采用降落伞轴向-径向动量守恒充气模型初步分析了大气密度对降落伞充气特性的影响[10]，结果发现当大气密度约低于地球海拔高度27km以上的稀薄程度时，大气密度对降落伞的充气时间、充气距离和降落伞张开的变化特征均开始存在较大的影响，不可忽略，且随着大气密度的进一步减少，影响越来越大。因此，本文在文献[10]的研究基础上，又作了进一步的分析，特别是针对火星大气密度对充气过程中伞衣面积变化的影响规律作了半定量化的分析，以便在对火星探测着陆系统的整个工作过程进行数值仿真或物伞系统的动力学特性研究或性能评定时，为较为准确地采用降落伞的充气时间和充气过程中伞衣面积随时间的变化规律提供参考。

1 充气模型

根据Dean Wolf提出的轴向–径向动量守恒充气模型[11]，在充气模型的建立过程中，作如下基本假设：

1）在充气过程中，物体和降落伞的飞行弹道相同；

2）在充气过程中，伞衣阻力系数不变；

3）在充气过程中，空气密度不变；

4）完全充满后，伞衣为半球形；

5）充气期间，伞衣形状如图1所示，由一个半径为的半球和一个上底直径为2、下底直径为2的倒截锥所组成。

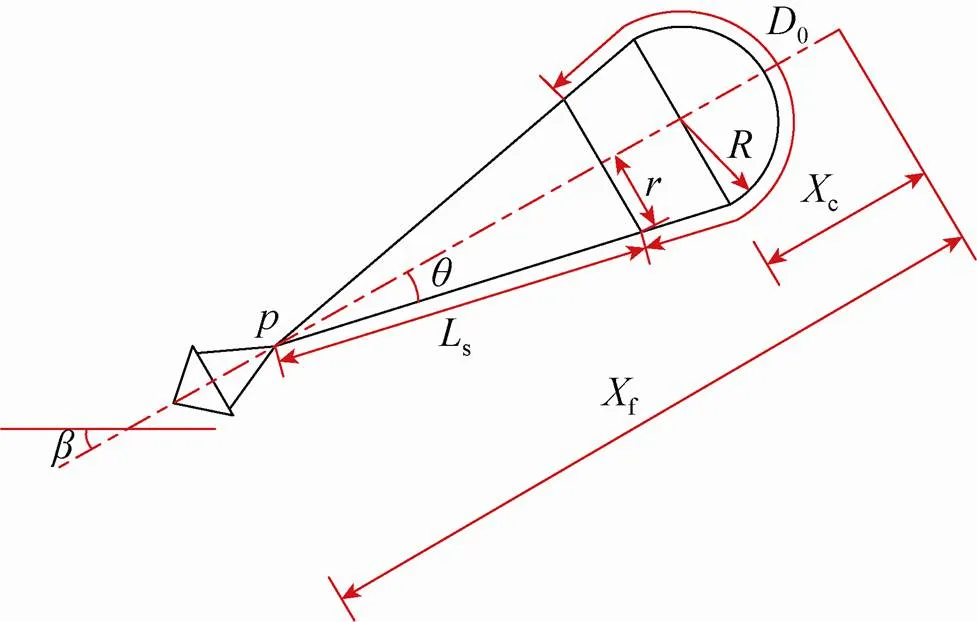
图1 伞衣几何形状及弹道坐标

图中为弹道倾角；为伞绳交汇点；为伞绳与降落伞轴线间夹角；s为伞绳长度；0为降落伞名义直径；c为伞衣运动距离；f为物体运动距离。

根据变质量动量方程，在飞行弹道的切向，物体和降落伞的运动方程有

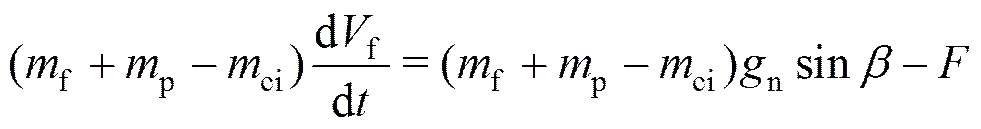
（2）

式中f为物体的质量；p为降落伞的质量；ci为已充气部分的伞衣质量；f为物体的瞬时轴向速度；为轴向力；a为降落伞的轴向附加质量；c为降落伞的瞬时轴向速度；c为动压；D为以充气伞衣的投影面积为参考面积的阻力系数；c为伞衣的投影面积；为时间；n为地球重力加速度。

由飞行弹道的法向动量守恒可得到弹道倾角变化率的表达式为

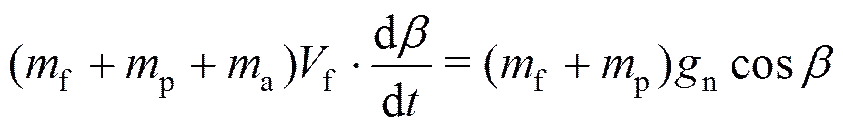
根据充气伞衣的径向运动方程有

（4）

式中r为径向附加质量；r为伞衣径向速度；R为径向力系数；其取值参考文献[11]。

同时假设伞绳是非弹性的，则从伞绳汇交点到伞衣充气最大圆周的距离可根据几何关系表示为

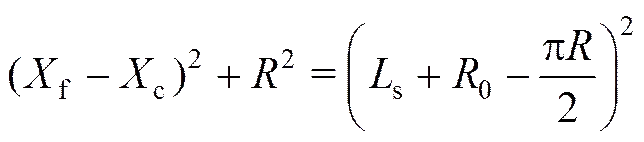
式中0=0/2。

通过式（5）两边对进行两次求导后，再与式（1）~（4）式组成微分方程组，并进行求解即可考察开伞速度、大气密度和伞衣直径对降落伞充气时间、充气距离、充气过程中伞衣面积变化的影响。

为了充分验证上述充气模型分析降落伞充气性能的可行性和正确性，文献[10]中曾采用本模型分别对名义直径为8.5m的C-9型标准平面圆伞和名义直径为12.2m的盘–缝–带伞在几种试验条件下的一些充气性能进行了计算，并与试验情况或经验公式所表示的结果进行了对比，验证了本充气模型用于分析降落伞充气性能是可行的，也是正确的。由于篇幅所限且文献[12]中已提供了C-9型标准平面圆伞的部分验证结果，在此只补充名义直径为12.2m的盘–缝–带伞在两种高度试验状态下的分析情况。根据文 献[13]其试验初始条件如表1，降落伞的基本结构参数参见文献[14]，阻力系数参考文献[11,15]。利用上述充气模型对两种状态下开伞载荷的变化和充气时间进行了计算，最大开伞载荷和充气时间均与文 献[13,16-17]试验结果（如表2）基本吻合。这也证明了上述充气模型的正确性。

表1 试验初始条件

Tab.1 Initial parameters of test

表2 计算和试验结果对比

Tab.2 Comparison of calculation and test results

2 大气密度对充气性能的影响与分析

为了便于与一些试验结果进行比较验证，在进行大气密度对降落伞充气性能的影响分析过程中，仍然以验证模型的12.2m盘–缝–带伞及其试验条件[13]为基准，选取了0.14kg/m3、0.028kg/m3、0.014kg/m3、0.002 8kg/m3、0.001 4kg/m3五种大气密度进行研究。

2.1 大气密度对充气时间的影响

降落伞的充气时间随大气密度的变化情况如图2。从中可以看出，降落伞的充气时间，在大气密度较大时对大气密度不太敏感；但在大气密度小到一定程度后，如达到接近火星表面的大气密度水平（约为0.015kg/m3）时，随着大气密度的减小，充气时间急剧增大。

2.2 大气密度对充气距离的影响

降落伞的充气距离随大气密度的变化情况如图3。从图中同样可以看出，降落伞的充气距离，在大气密度较大时对大气密度不太敏感；但在大气密度小到一定程度后，如达到接近火星表面的大气密度水平（约为0.015kg/m3）时，随着大气密度的减小，充气距离也急剧增大。

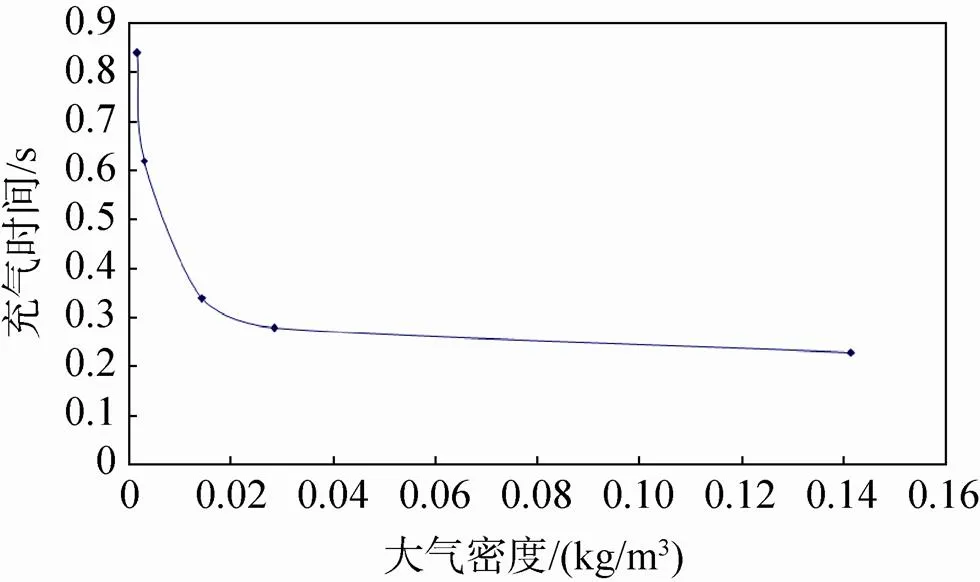
图2 充气时间与大气密度间的关系

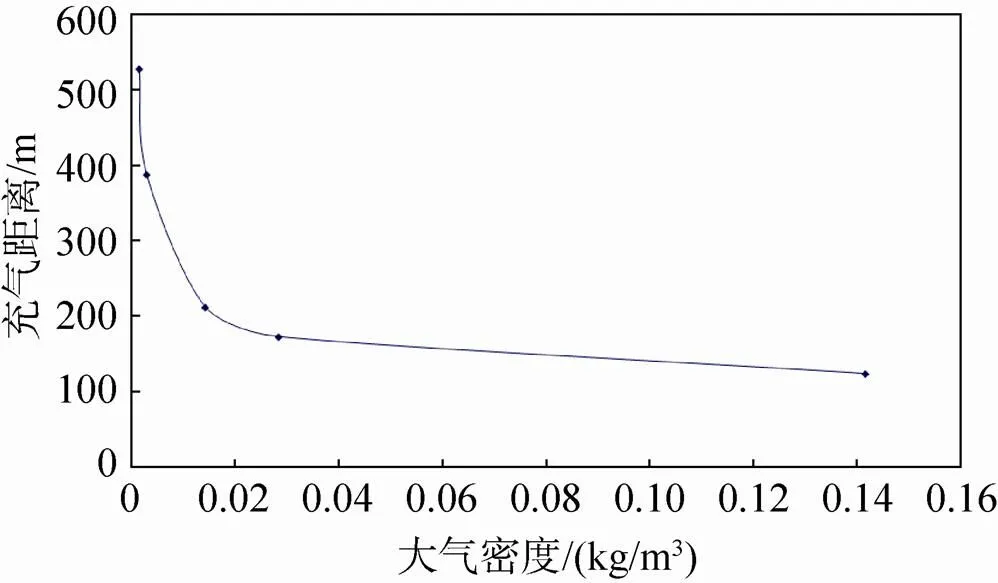
图3 充气距离与大气密度间的关系

2.3 大气密度对伞衣张开速度的影响

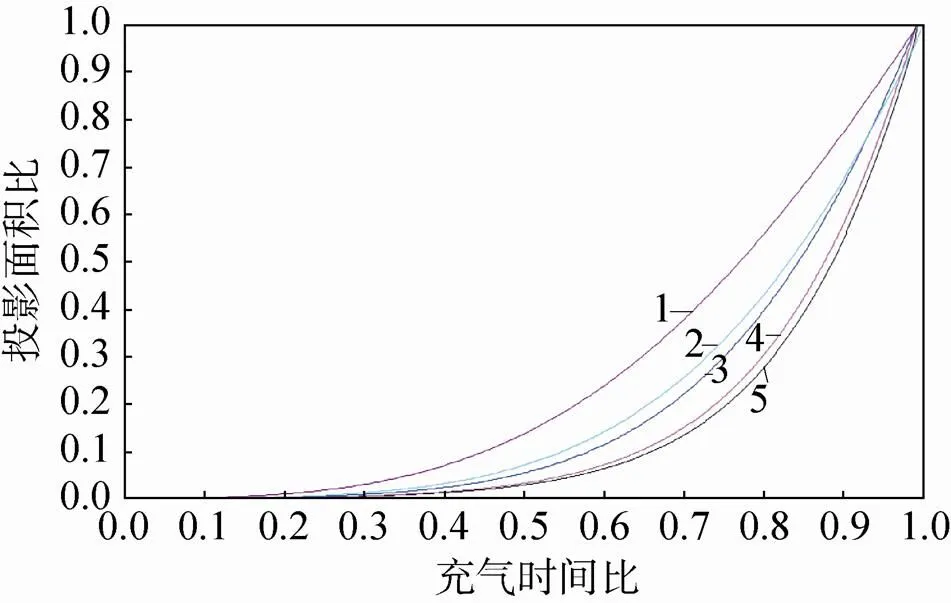
图4~6分别是伞衣张开半径变化、伞衣投影面积变化和伞衣投影面积比（充气过程中的伞衣投影面积与充满后的投影面积之比）变化与大气密度间的关系。从中可以看出，在大气密度较低的情况下，降落伞的张开是开始时非常缓慢，然后再快速张开；而在大气密度较高的情况下，伞衣一开始就张开得比较快。在稀薄大气开伞过程中投影面积比随时间变化的曲率要比高密度大气中的大些，或者说如果将投影面积比看成是归一化时间（本文为充气时间比，即充气过程中时间与伞衣充满时间之比）的幂函数，则在稀薄大气开伞过程中投影面积比随归一化时间变化的幂指数要大些。图7是表1中两种试验条件下的投影面积比随归一化时间的变化情况，其结果也同样如此。

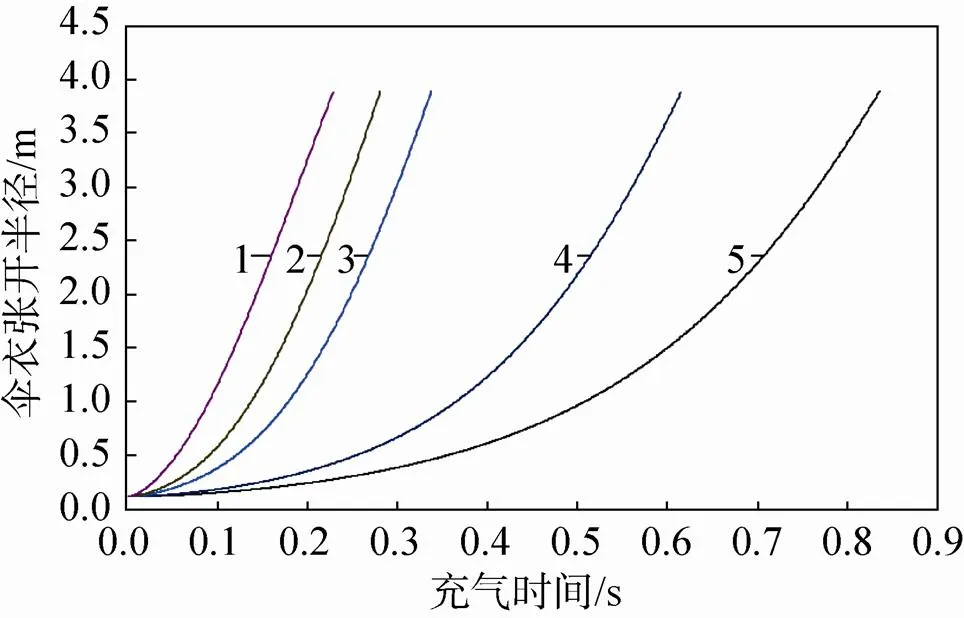
大气密度/(kg/m3)：1—0.14；2—0.028；3—0.014；4—0.002 8；5—0.001 4

大气密度/(kg/m3)：1—0.14；2—0.028；3—0.014；4—0.002 8；5—0.001 4

图5 伞衣投影面积变化与大气密度间的关系

Fig.5 The relationship between the canopy projection area change and the atmospheric density

大气密度/(kg/m3)：1—0.14；2—0.028；3—0.014；4—0.002 8；5—0.001 4

开伞高度/m：1—42 500；2—3 164

图7 两种试验状态下的投影面积比变化情况

Fig.7 Projected area ratio changes under two test conditions

2.4 结果分析

针对上述各计算结果，综合分析如下：

1）造成降落伞的充气时间、充气距离、伞衣张开半径和投影面积变化等性能随大气密度上述变化的主要原因是由于在开伞速度相同的情况下，大气密度越低，其动压就越小，在伞衣张开过程中，作用在单位面积伞衣上的径向力也就相应减小，当径向力小到一定程度时，伞衣质量的变化对伞衣径向张开速度的影响就相对变得比较明显了，从而也比较明显地影响充气时间和充气距离；而在大气密度较大的时候，伞衣上的径向力一般均比较大，因而伞衣质量的变化对充气时间和充气距离的影响也就较小。或者说，伞衣质量对充气时间和充气距离的影响要在大气密度小到一定程度后才能体现出来[10]。图8是曾利用上述充气模型所计算某型伞[18]在两种大气密度下伞衣质量变化对充气时间的影响。从中可以看出，在大气密度较大的情况下，伞衣质量对充气时间的影响不大；而在大气密度较小的情况下，则随着伞衣质量的增大，充气时间增大。

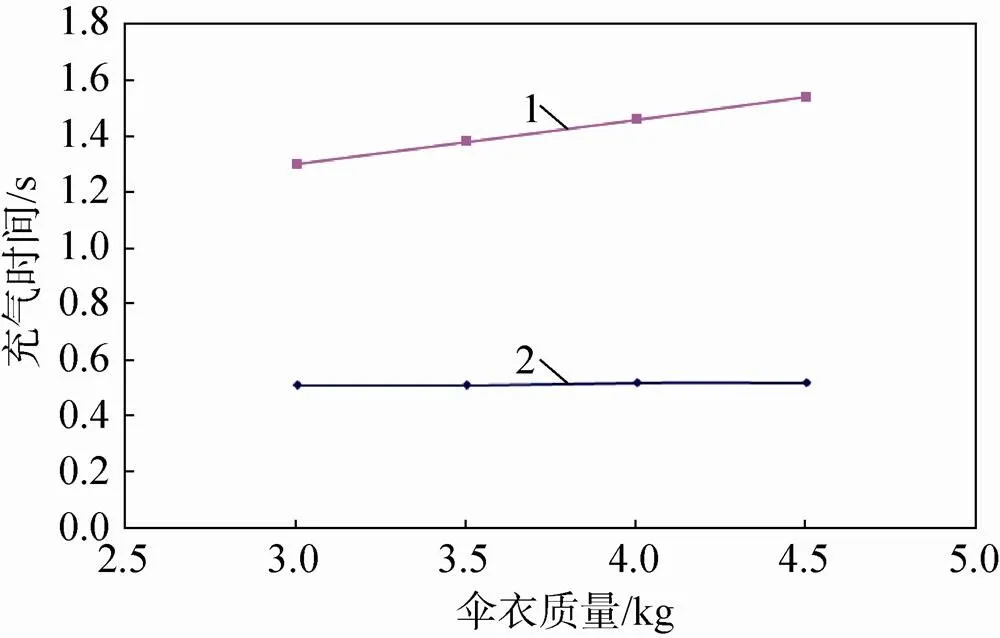
大气密度/(kg/m3)：1—0.012 25；2—0.612 5

2）根据图2可知，在大气密度较大时，降落伞的充气时间对大气密度的变化不太敏感。在目前降落伞充气时间的一般经验公式（6）中也没有体现出大气密度对充气时间的影响[8]，因此这一规律与经验公式所表示的是相吻合的。

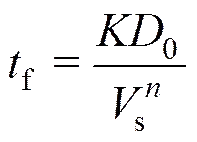
式中f为充气时间；为比例常数；0为降落伞直径；s为开伞速度；为充气时间指数。而在大气密度较小时，如达到接近火星表面的大气密度水平（约为0.015kg/m3）时，降落伞的充气时间则对大气密度的变化非常敏感（如图2），这是经验公式（6）中未能反映出来的。因此，在火星如此稀薄的大气环境中，经验公式（6）将不再适用。

3）根据图3可知，在大气密度较大时，降落伞的充气距离对大气密度的变化不太敏感。目前降落伞充气距离的一般经验公式（7）也没有体现出大气密度对充气距离的影响[9]，因此这一规律与经验公式所表示的是相吻合的。

式中f为充气距离；为比例常数；0为降落伞直径。而在大气密度较小时，如达到接近火星表面的大气密度水平（约为0.015kg/m3）时，降落伞的充气距离则对大气密度的变化非常敏感（如图3），这是经验公式（7）中未能反映出来的。因此，在火星如此稀薄的大气环境中，经验公式（7）将不再适用。

4）对图5中的几个不同大气密度状态下的伞衣投影面积P随充气过程中的时间变化曲线进行数据拟合，得到其关系如表3所示，可以发现在火星稀薄大气环境中，伞衣投影面积为充气时间的4次多项式关系，这和美国高空开伞试验所得到的规律相同[19]。因此，目前在开伞载荷的计算过程中，一般将伞衣阻力面积假设为时间的2~3次多项式关系[9]，这在火星稀薄的大气环境中将不再适用。

表3 伞衣投影面积随时间变化曲线的拟合关系

Tab.3 The canopy projection area of curve fitting relationship over time

3 结束语

综合上述计算分析，可以看出：

目前有关降落伞充气性能（如充气时间、充气距离、伞衣阻力面积变化）的一些经验关系式对于火星这种稀薄大气环境将不再适用。在火星稀薄的大气环境下，降落伞的充气时间、充气距离随大气密度的减小将急剧增大；伞衣阻力面积为充气过程中时间的4次多项式关系。

[1] LAU R A, HUSSONG J C. The Viking Mars Lander Decelerator System[C]//AIAA Aerodynamic Deceleration Systems Conference, Dayton, Ohio: AIAA, 1970: 1-15.

[2] THURMAN S W. Return to the Red Planet: An Overview of the Mars Pathfinder Mission[C]//13th Aerodynamic Decelerator Systems Technology Conference, Clearwater Beach, FL: AIAA, 1995: 24-31.

[3] RONCOLI R B, LUDWINSKI J M. Mission Design Overview for the Mars Exploration Rover Mission[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, California: AIAA, 2002: 1-24.

[4] GROVER M R, CICHY B D, DESAI P N. Overview of the Phoenix Entry, Descent and Landing System Architecture[J]. Journal of Spacecraft and Rockets, 2011, 48(5): 706-712.

[5] SENGUPTA A, STELTZNER A, WITKOWSKI A, et al. An Overview of the Mars Science Laboratory Parachute Decelerator System[C]//19th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Williamsburg, VA: AIAA, 2007: 1-8.

[6] WILLCOCKSON W H. Mars Polar Lander Entry, Descent, and Landing Design[R]. AAS 99-302, 1999.

[7] UNDERWOOD J, BOWN N. An Entry, Descent, and Landing System for the Beagle 2 Mars Mission[C]//AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, Boston, MA: AIAA, 2013: 2001-2052.

[8] E. G. 尤因. 回收系统设计指南[M]. 北京: 航空工业出版社, 1988.EWING E G. Design Guidelines for Recycling System[M]. Beijing: Aviation Industry Press, 1988. (in Chinese)

[9] 王利荣, 降落伞理论与应用[M]. 北京: 宇航出版社, 1997. WANG Lirong. Theory and Application of Parachute[M]. Beijing: China Astronautic Publishing House, 1997. (in Chinese)

[10] 荣伟. 火星探测器减速着陆技术研究[D]. 北京: 中国空间技术研究院, 2008. RONG Wei. The Study on Mars Exploration Deceleration Landing Technology[D]. Beijing: China Academy of Space Technology, 2008. (in Chinese)

[11] WOLF D. A Simplified Dynamic Model of Parachute Inflation[J]. Journal of Aircraft, 2015, 11(1): 28-33.

[12] 荣伟, 陈旭, 陈国良. 大气密度对降落伞充气性能的影响[J]. 航天返回与遥感, 2006, 27(3): 11-16. RONG Wei, CHEN Xu, CHEN Guoliang. The Effect of Atmospheric Density on Parachute Inflation Performances[J]. Spacecraft Recovery & Remote Sensing, 2016, 27(3): 11-16. (in Chinese)

[13] MURROW H N, ECKSTROM C V. Low and High-altitude Tests of Parachutes Designed for Use in Low-density Atmospheres[C]//3rd Aerodynamic Deceleration Systems Conference, New York: AIAA, 1970: 1164.

[14] WHITLOCK C H, BENDURA R J. Inflation and Performance of Three Parachute Configuration from Supersonic Flight Tests in a Low-density Environment[R]. NASA TN D-5296, Washington: NASA Langley Research Center, 1969.

[15] TALAY T A. Parachute Deployment Parameter Identification Based on an Analytical Simulation of Viking BLDT AV-4[R]. NASA TN D-7678, Washington: NASA Langley Research Center, 1974.

[16] ECKSTROM C V, PREISSER J S. Flight Test of a 40-foot-nominal-diameter Disk-gap-band Parachute Deployed at a Mach Number of 1.91 and a Dynamic Pressure of 11.6 Pounds Per Square Foot[R]. NASA TM X-1575, Washington: NASA Langley Research Center, 1968.

[17] ECKSTROM C V, MURROW H N. Flight Tests of Cross, Modified Ringsail, and Disk-gap-band Parachutes From a Deployment Altitude of 3.05Km (10 000ft)[R]. NASA TM X-2221, Washington: NASA Langley Research Center, 1971.

[18] BARNARD G A. The Effect of Extreme Altitude on Parachute Filling Distance[C]//Aerospace Design Conference, Irvine, CA: AIAA, 2013: 54-61.

[19] FALLON Ⅱ E J. System Design Overview of the Mars Pathfinder Parachute Decelerator Subsystem[C]//14th Aerodynamic Decelerator Systems Technology Conference, San Francisco, CA: AIAA, 1997: 341-358.

（编辑：庞冰）

The Primary Studies on the Effect of Martian Atmosphere on Parachute Inflation Performances

RONG Wei BAO Jinjin

（Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China）

Mars has been one of the hot spots of human deep space exploration. Because of the presence of the atmosphere on Mars, the parachute has been an important deceleration device to ensure the safety of the Mars explorer landing on the surface of Mars. However, due to the density of the atmosphere on Mars is very thin, the mastery of parachute inflation performance in the Martian atmosphere environment is a key point to the descent and landing system of Mars explorer in the engineering design, and it is also a key point to establish the parachute-load system opening dynamic model in the Martian environment or numerical simulation system in order to evaluate the performance of the descent and landing system of Mars explorer. With using the parachute inflation model of axial-radial momentum conversation, the influence of atmosphere density on parachute inflation performance is studied, including parachute inflation time, inflation distance and canopy project area. The results show that some experiential formulas can not adapt to the Martian environment, the parachute inflation time and inflation distance increases rapidly with air density decrease in the Martian atmosphere; the variety of the canopy area during parachute inflation is a quartic polynomial with the inflation time. These research results are important and valuable for engineering design, test and evaluating performance of the descent and landing system of Mars explorer.

canopy area; inflation distance; Inflation time; Parachute; Atmosphere density; Martian atmosphere; deep space exploration

V476.4

A

1009-8518(2017)04-0001-07

10.3969/j.issn.1009-8518.2017.04.001

荣伟，男，1969年生，2008年获中国空间技术研究院飞行器设计专业工学博士学位，研究员，博士生导师。研究方向为航天器回收着陆技术。E-mail：rongweilxl@163.com。

包进进，女，1984年生，2011年获中国空间技术研究院航天器返回与着陆专业硕士学位，工程师。研究方向为航天器回收着陆技术。E-mail：bjj0524@163.com。

2016-12-09