平均非扩张映射的迭代程序的收敛性
廖怡娜,张创亮
(广东工业大学 应用数学学院,广州 510520)
平均非扩张映射的迭代程序的收敛性
廖怡娜,张创亮
(广东工业大学 应用数学学院,广州 510520)
利用Gocbel等人引入的平均非扩张映射的概念,得到了一致凸Banach空间下Mann迭代程序收敛于平均非扩张映射不动点的一些结果,同时也得到了在非凸Banach空间下迭代收敛的一些结果.
平均非扩张映射; Mann迭代程序; 不动点
0 引言
非扩张映射在泛函分析中是一类非常重要的非线性映射.近几十年来,关于非扩张映射的不动点的存在性问题的研究已取得丰富的成果.在一致凸 Banach空间E中,C是E的非空有界闭凸子集,则非扩张映射T: C→C有不动点.这是一个众所周知的结果.1953年,Mann[9]为了研究不动点逼近问题,引入了迭代程序
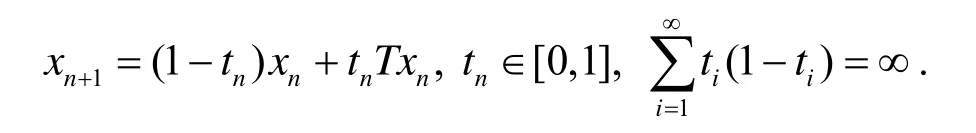
后来,Krasnosel'skii[11]和Dotson[10]等人对这种迭代方法进行进一步研究,证明了在凸空间下迭代程序的收敛性,可以找到非扩张映射的不动点.1976年,Ishikawa[5]利用广义 Mann序列迭代证明了在任意Banach空间下非扩张映射的收敛定理.2007年,Gocbel和Japon Pineda[1]引入平均非扩张映射,平均非扩张映射是非扩张映射的推广,其它结论见文[2,3,4].
本文将Mann迭代程序在非扩张映射下的一些结果推广到平均非扩张映射上.
定义1[1,2]设E是Banach空间,C是E的非空子集,若映射T: C→E满足
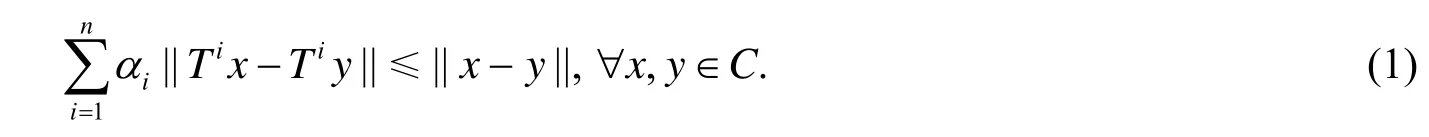
定义2 设E是Banach空间,C是E的非空子集,称映射T: C→E是半紧的,是指对任意的有界序列使得则必存在的收敛子列.
引理 1[3]设E是 Banach空间,C是E的非空闭凸子集,若T: C→E是平均非扩张映射,且
引理 2[3]设E是 Banach空间,C是E的非空闭凸子集,T: C→C是平均非扩张映射,且若是C中有界列,则当且仅当
引理 3[5]设E是Banach空间,C是E的非空子集,T: C→C是非扩张映射.对于有界序列和实数列若
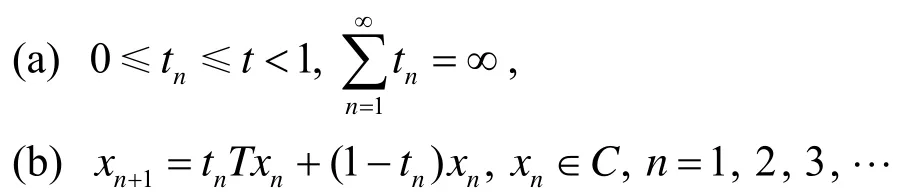
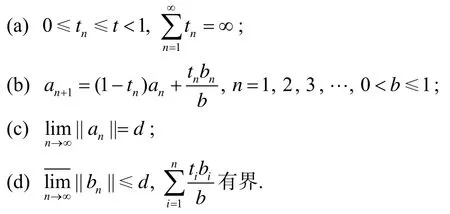
则d=0.
证明 与文[7]中引理2的证明方法类似.这里从略.
1 主要结果
定理 1 设E是一致凸 Banach空间,C是E的非空闭凸子集,T: C→C是具有不动点的平均非扩张映射,并且满足和半紧性.对于C中序列和实数列若
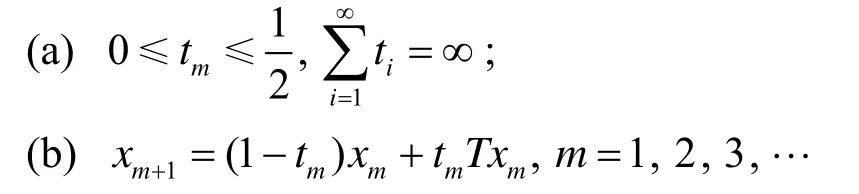
证明 因为T有不动点,从而 fix(T)≠Ø.根据引理 1可以知道对任意固定z∈fix(T),有
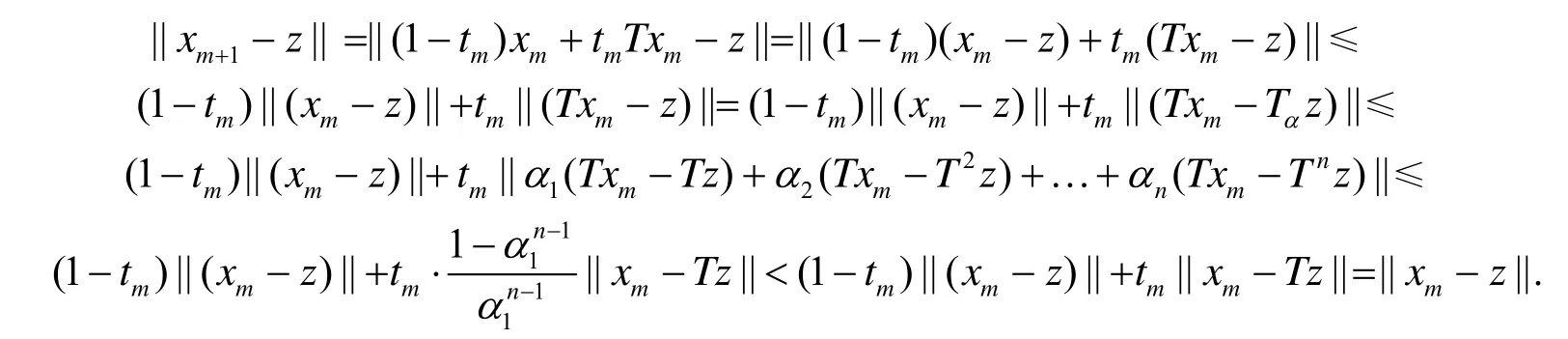
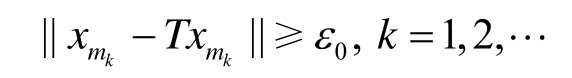
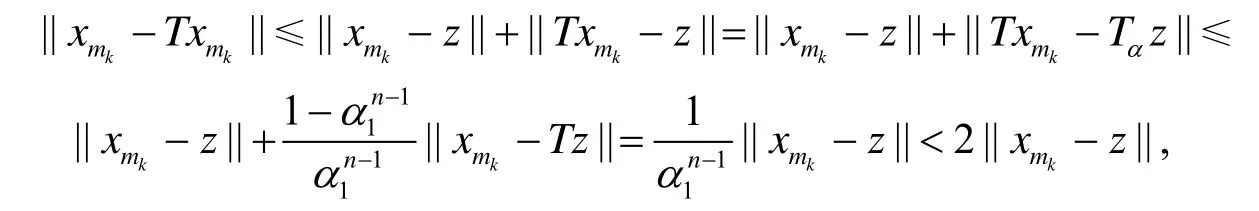
从而可得

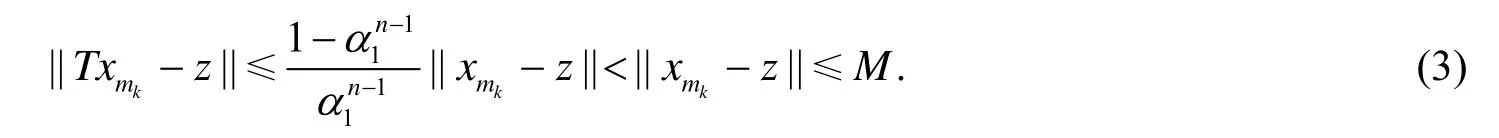
由式(2)、(3)可以推出
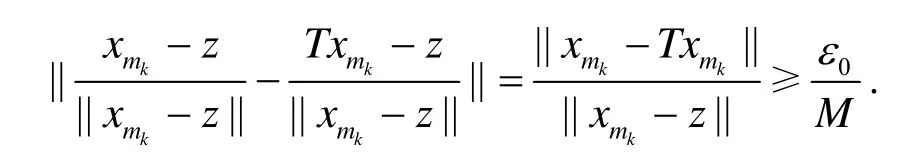
另一方面,注意
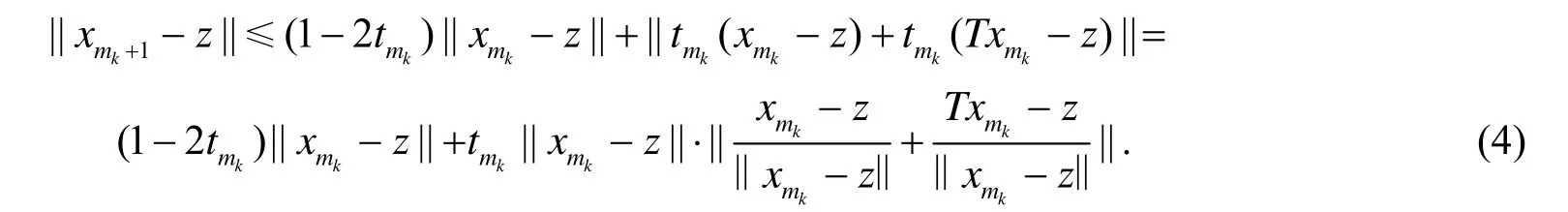
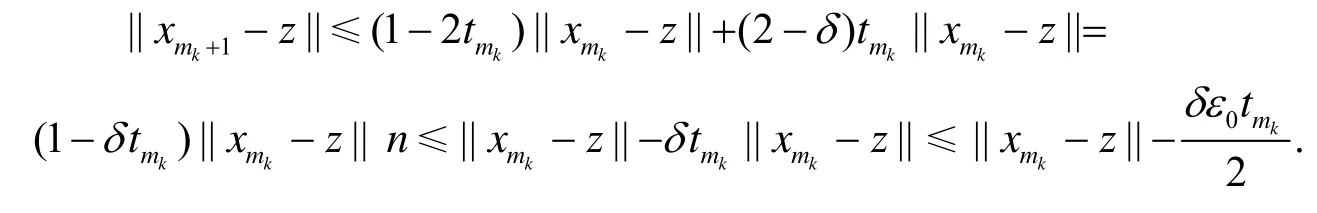
因此
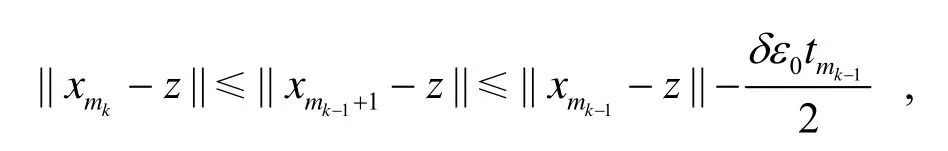
故有
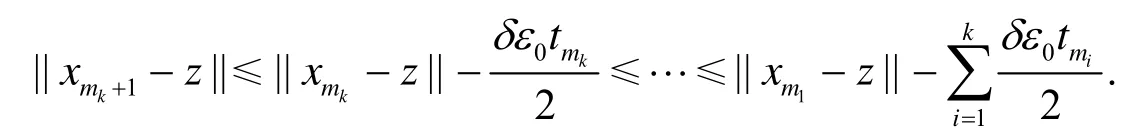
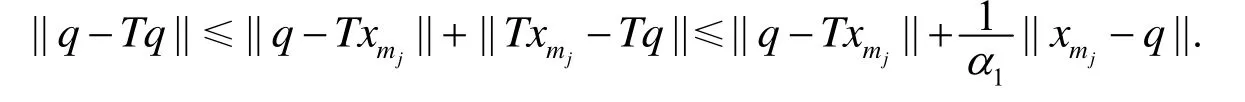

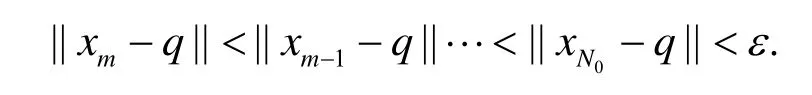
定理2 设E是Banach空间,C⊂E是非空闭凸子集,T: C→C是具有不动点的平均非扩张映射,并且满足和半紧性,对于C中的有界序列和实数列若
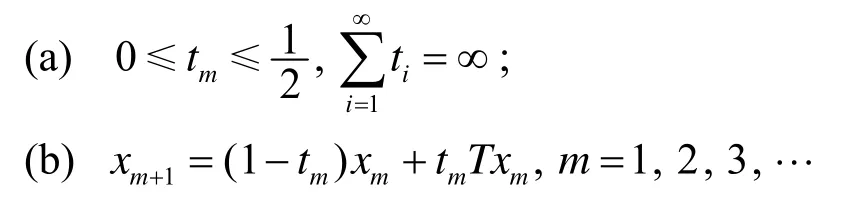
则xm收敛T的不动点.
证明 由于Tα是非扩张映射,根据引理3可以知道因为由引理2可以知道又是有界序列,T是半紧的,从而可知有收敛子列设容易知道以下仿照定理1的证明,可以得到
推论 1 设E是 Banach空间,C是E的非空有界闭凸子集,T: C→C是平均非扩张映射,并且满足和半紧性,对于C中序列和实数列若
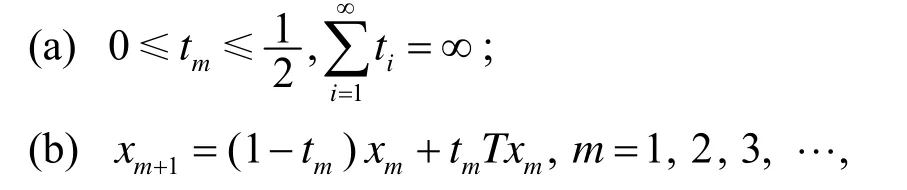
则xm收敛T的不动点.
注2 当α1=1,定理2就是文[5]中定理2的推广.
定理 3 设E是 Banach空间,C是E的非空闭凸子集,T: C→C是具有不动点的平均非扩张映射且满足和半紧性,对于C中序列和实数列若
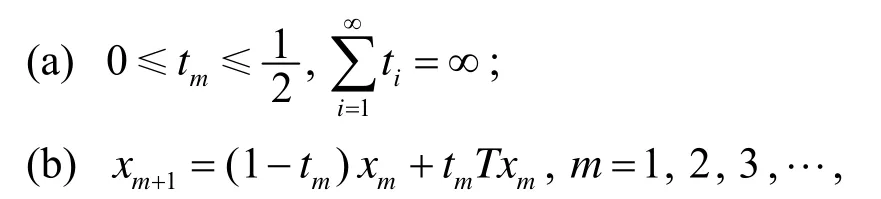
证明 必要性是显然的.下面证明充分性.

从而
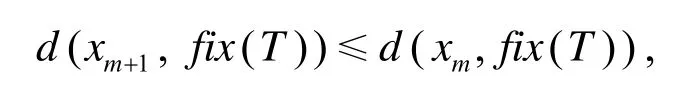
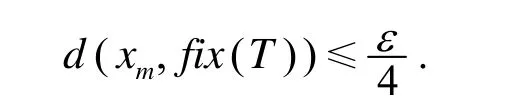
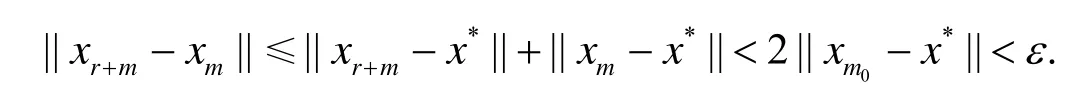
注3 定理3没有假设T的半紧性,但加强了条件假设.
定理4 设E是Banach空间,C是E的非空子集,T: C→E是平均非扩张映射,且α1>0.对于C中的有界序列和实数列若
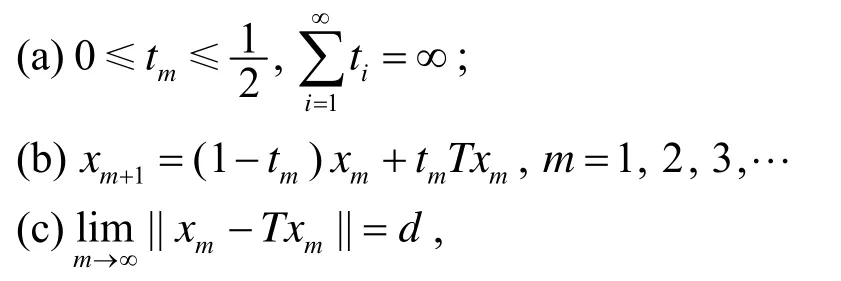
则d=0.
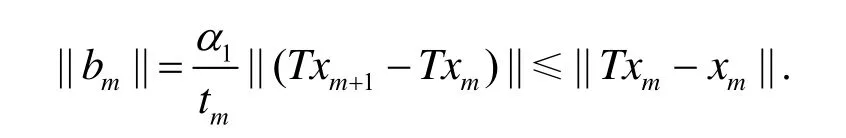

故由引理4可知d=0.
注4 定理4把[5]中引理2的结果推广到平均非扩张映射上.
2 结束语
本文研究了一类平均非扩张映射的Mann序列的迭代收敛性,改进和发展了文[5]和文[9]的一些结果.值得思考的问题是: 在平均非扩张映射下,对于Ishikawa迭代程序,是否也有类似的结果?
[1]Goebel K.,Pineda M A.On a type of generalized nonexpansiveness[A].Proc.of the 8th International Conference on Fixed Point Theory and its Application.,2007(74): 660~665
[2]Piasecki L.Classification of Lipschitz Mappings[M].CRC Press,2013
[3]Klin-eam C.,Suantai S.Fixed point theorems for -nonexpansive mappings[J].Appl.Math.Lett.,2010(23): 728~731
[4]Gallagher T.M.The demiclosedness principle for mean nonexpansive mappings[J].Math.Analysis and Appl.,2016(439): 832~842
[5]Ishikawa S.Fixed points and iteration of a nonexpansive mapping in a Banach space[J].Proc.Amer.Math.Soc.,1976(59): 65~71
[6]Ishikawa S.Fixed points by a new iteration method[J].Proc.Amer.Math.Soc.,1974(44):147~150
[7]Deng L.Convergence of the Ishikawa Iteration Process for Nonexpansive Mappings[J].Math.Analysis and Appl.,1996(199): 769~775.
[8]Tan K.K.,Xu H.K.Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process[J].Math.Anal.Appl.,1993(178): 301~308
[9]Mann W.R.Mean value methods in iteration[J].Proc.Amer.Math.Soc.,1953(4): 506~510
[10]Dotson W.G.,Jr.On the Mann iterative process[J].Trans.Amer.Math.Soc.,1970(149): 65~73
[11]Krasnosel'skii M.A.Two remarks on the method of successive approximations[J].Uspekhi Mat.Nauk,1955(10): 123~127
Iterative Procedure Convergence for Mean Nonexpansive Mappings
LIAO Yina,ZHANG Chuangliang
(School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China)
We used the concept of mean nonexpansive mapping which are introduced by Gocbel et al ,and obtained some results of Mann iterative procedure converges to fixed point of mean nonexpansive mappings on uniformly convex Banach space,and got some results of iterative convergence for it’s on non-uniformly convex Banach space.
mean nonexpansive mappings,Mann iterative procedure,fixed point
O177.91 文献标识码: A 文章编号: 1672-5298(2017)02-0011-05
2017-03-12
廖怡娜(1992 -),女,广东梅州人,广东工业大学应用数学学院硕士研究生.主要研究方向: 系统与控制
张创亮(1992 -),男,广东梅州人,广东工业大学应用数学学院硕士研究生.主要研究方向: 非线性泛函分析

