关于p-凸函数的不等式
时统业,李 军
(海军指挥学院 信息系,南京 211800)
关于p-凸函数的不等式
时统业,李 军
(海军指挥学院 信息系,南京 211800)
已有文献证明了h-凸函数的h-左导数、h-右导数的存在性和单调性.p-凸函数是h-凸函数的特例,所以p-凸函数的单侧导数存在且单调.借助单侧导数建立了p-凸函数的积分不等式,从而得到p-凸函数的加权Hermite-Hadamard型不等式的加强.
p-凸函数; h-凸函数; Hermite-Hadamard型不等式; 积分不等式
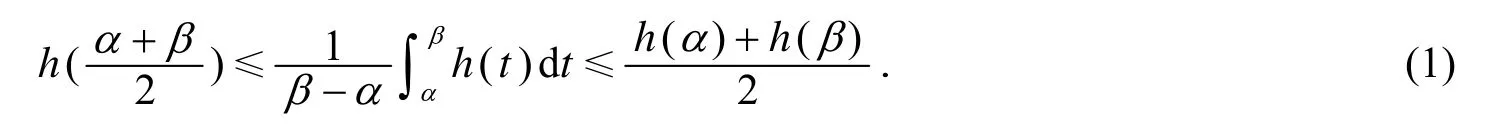
式(1)即Hermite-Hadamard不等式.
文[1,2]给出了由式(1)生成的两个差值的估计.
定理1[1,2]设h:[a,β]→ℝ是凸函数,则有
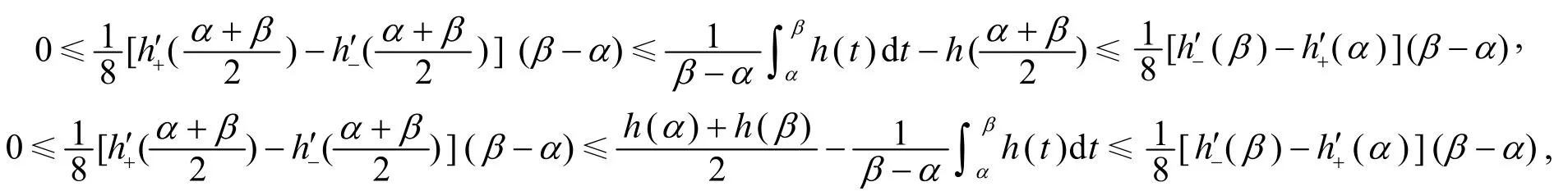
定理2[3]设是[a,b]上的凸函数,则有
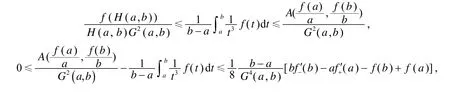
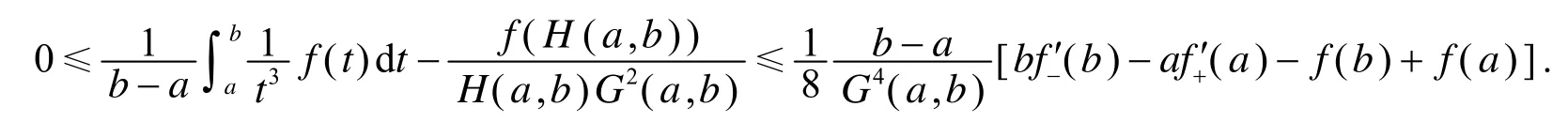
作为凸函数的推广,文[4]引入p-凸函数的概念.
定义 1[5]设I⊆ℝ,若对任意x1,x2∈I和任意则称I为p-凸集.
定义 2[4,5]设I(⊆ℝ)是 p-凸集,f:I→ℝ,若对任意x1,x2∈I和t∈[0,1],存在或使得
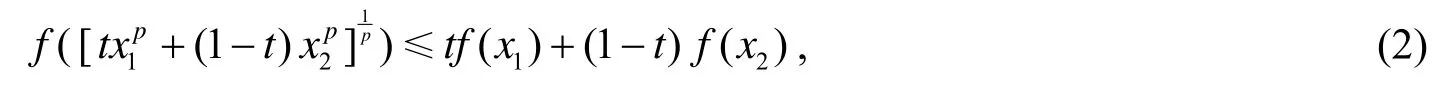
则称 f为I上的p-凸函数.若不等式(2)的不等号反向,则称f为I上的p-凹函数.
若f为I上的正的p-凸(凹)函数,则f-1是 I上的 MH-凹(凸)函数[6].
文[5]讨论了单调p-凸函数的性质.文[7]利用凸函数与p-凸函数的关系建立了p-凸函数的Hadamard型不等式.文[8]从p-凸函数的定义出发建立了p-凸函数的Hadamard型不等式.
定理3[7,8]设f是[a,b](⊂(0,+∞))上的p-凸函数,则有
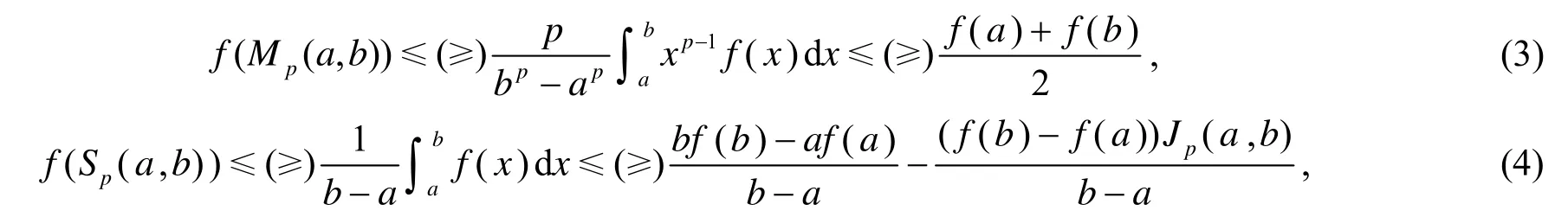

2001年,王良成在文[12]中引入了h-凸函数和h-导数的概念.
定义 3[12]设 h是[a,b]上的连续严格递增函数,f是定义在[a,b]上的函数,若对任意时,有

则称f是[a,b]上的h-凸函数.
定义 4[12]设x0∈(a,b),若极限存在,则称之为 f在x0处关于 h的左(右)导数,记为此时称f在x0处关于h-左(右)可导.
通常的凸函数就是h(x)=x时的 h-凸函数.一些由二元幂平均给出的凸函数对应着 h-凸函数.比如可以证明,f为调和平方凸函数[13]当且仅当是-凸的.f为 GH-凸函数[14]当且仅当是lnx-凸的.p-凸函数就是当h(x)=xp时的 h-凸函数,这是因为对任意有式(2)成立当且仅当对任意当 x1<x<x2时,有式(5)成立.
由于 p-凸函数是凸函数的推广,一个自然的想法就是将关于凸函数的结果推广到 p-凸函数.本文仿照文[1]的方法,建立p-凸函数的Hermite-Hadamard型不等式.为此,需先证明p-凸函数的单侧导数的存在性和单调性,并建立 p-凸函数与其单侧导数的联系,这只需要利用文[12]的结果.综合文[12]的性质和定理,有下面的
引理1[12]设f是[a,b]上的h-凸函数,则

(ⅰ)f在(a,b)内各点处的单侧导数存在;
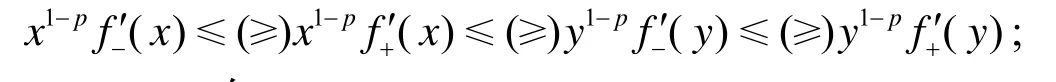
(ⅲ)对任意 x∈[a,b],y∈(a,b),有
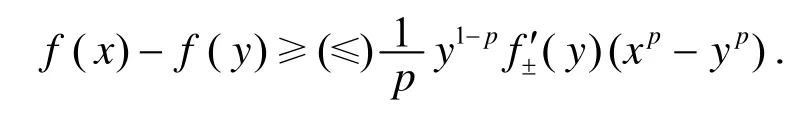
受文[3]的启发,有下面的
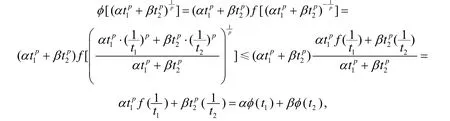
本文所采用的思想方法还可参见文[15]和[16].
主要结果
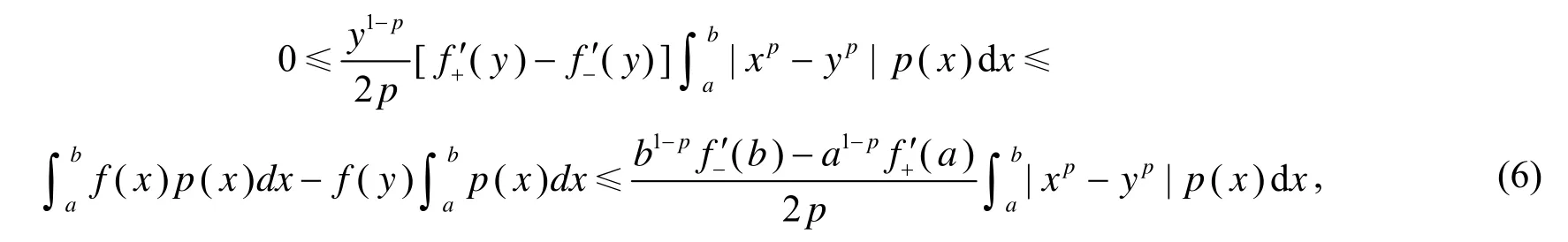
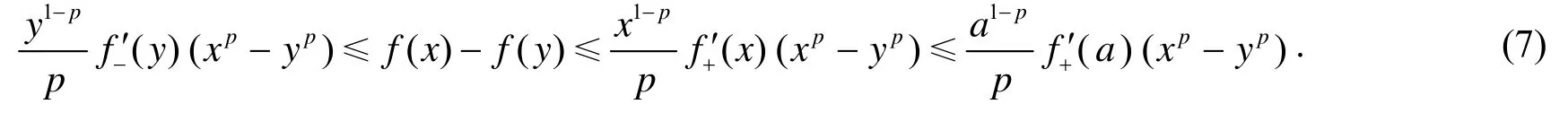
对任意 x∈[y,b],有
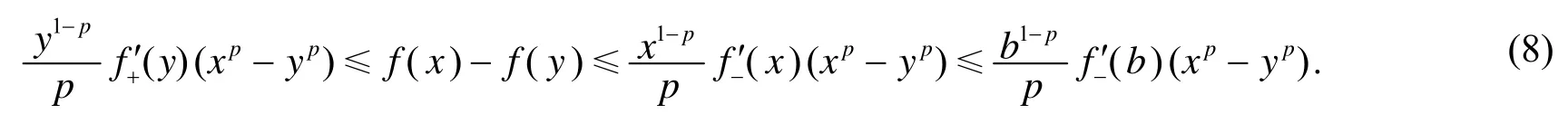
将式(7)和式(8)乘以p(x),分别在[a,y]和[y,b]上对x积分,然后将所得的两个不等式相加,注意到
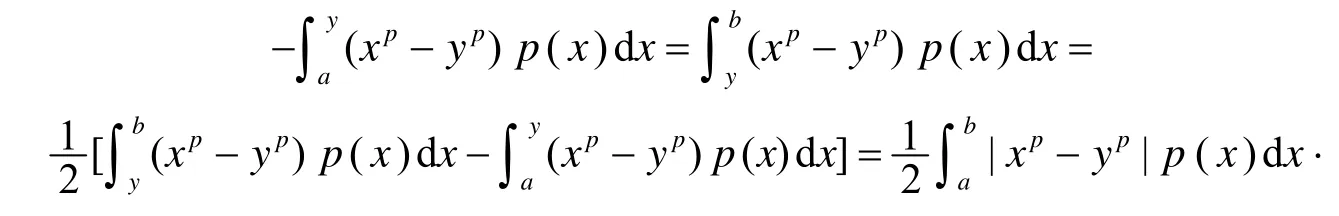
式(6)得证.
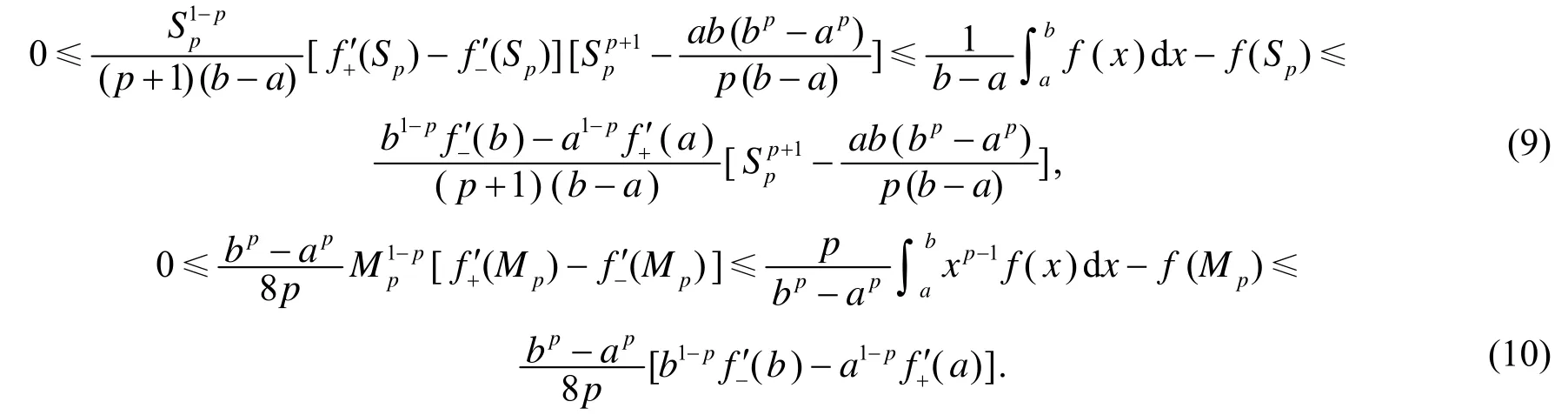
注1 由式(9)和式(10)得到定理3所给p-凸函数的Hadamard型不等式左边部分的加强.
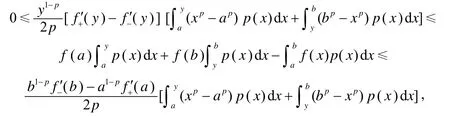
证明 由引理2(ⅱ)知式(11)的左边不等式成立.由引理2(ⅲ),对任意x∈[a,y],有

对任意x∈[y,b],有
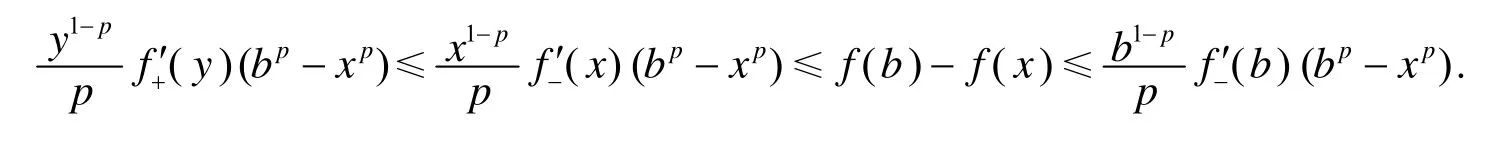
以下证明类似于定理4,这里从略.
推论2 设f是[a,b](⊂(0,+∞))上的p-凸函数,且皆存在,则有

注2 由式(11)和式(12)得到定理3所给p-凸函数的Hadamard型不等式右边部分的加强.
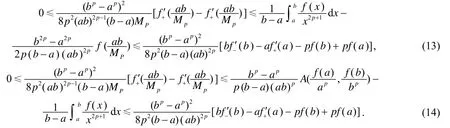
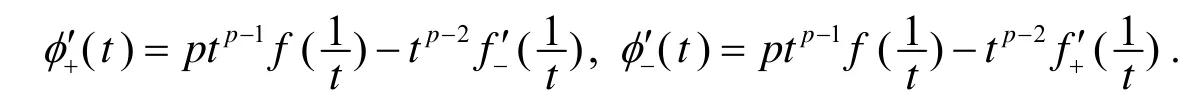
注3 式(13)和式(14)是定理2所给凸函数的不等式在p-凸函数中的推广.
[1]Dragomir S S.An inequality improving the first Hermite-Hadamard inequality for convex functions defined on linear spaces and applications for semi-inner products[J].J.Inequal.Pure Appl.Math,2002,3(2): 775~788
[2]Dragomir S S.An inequality improving the second Hermite-Hadamard inequality for convex functions defined on linear spaces and applications for semi-inner products[J].J.Inequal.Pure Appl.Math,2002,3(3): Article 35
[3]Dragomir S S,Gomm I.Companions of Hermite-Hadamard inequality for convex functions (I)[J].Scientia.Series A: Mathematical Sciences,25.17~25
[4]张孔生,万建平.p-凸函数及其性质[J].纯粹数学与应用数学,2007,23(1): 130~133
[5]宋振云.p-凸函数的几个性质[J].湖北职业技术学院学报,2010.13(1): 102~104
[6]宋振云.MH-凸函数及其Jensen型不等式[J].杭州师范大学学报(自然科学版),2015,14(2): 156~160
[7]宋振云,涂琼霞.p-凸函数的Hadamard型不等式[J].高师理科学刊,2010,30(6): 47~48
[8]宋振云,涂琼霞.关于p-凸函数的Hadamard型不等式[J].纯粹数学和应用数学,2011,27(3): 313~317
[9]匡继昌.常用不等式[M].第4版.济南: 山东科学技术出版社,2010: 53
[10]萧振纲,张志华.n个正数的Stolarsky平均[J].岳阳师范学院学报(自然科学版),2001,14(4): 5~8
[11]杨镇杭.对数指数平均的Hölder,Minkowski,Tchebychef 型不等式[J].徐州师范大学学报(自然科学版),2005,23(1): 31~34
[12]王良成.h凸函数[J].达县师范高等专科学校学报(自然科学版),2001,11(2): 8~10
[13]宋振云,陈少元.调和平方凸函数及其Jensen型不等式[J].首都师范大学学报(自然科学版),2015,36(3): 7~14
[14]陈少元.GH-凸函数及其Jensen型不等式[J].首都师范大学学报(自然科学版),2013,34(5): 1~5
[15]张小明,褚玉明.解析不等式新论[M].哈尔滨: 哈尔滨工业大学出版社,2009
[16]Dragomir S S,Pearce C E M.Selected Topics on Hermite-Hadamard inequalities and applications[D].Victoria: Victoria University,2000
Inequalities for p-Convex Functions
SHI Tongye,LI Jun
(Department of Information,PLA Naval Command College,Nanjing 211800,China)
The existing literatures have shown that the left and right h-derivatives for h-convex functions are monotone.p-convex functions is a special case of h-convex functions,so unilateral derivatives of p-convex functions are monotone.With the aid of unilateral derivatives,we established inequalities for p-convex functions,and obtain weighted Hermite-Hadamard type inequalities for p-convex functions.
p-convex function,h-convex function,Hermite-Hadamard type inequality,integral inequality
O178 文献标识码: A 文章编号: 1672-5298(2017)02-0001-05
2017-02-26
时统业(1963-),男,河北张家口人,硕士,海军指挥学院信息系副教授.主要研究方向: 基础数学

