Taylor展开随机径向基点插值无网格法在随机非稳态热传导中的应用
赵玉凤
(山西工商学院 基础教学部,山西 太原 030006)
Taylor展开随机径向基点插值无网格法在随机非稳态热传导中的应用
赵玉凤
(山西工商学院 基础教学部,山西 太原 030006)
用Taylor展开随机径向基点插值无网格法(TSRPIM)对随机温度场进行了分析.径向基点插值是一种新型的无网格法,采用耦合径向基函数和多项式基函数构造近似函数,有效地解决了点插值中系数矩阵奇异性问题,而且由于插值具有Delta函数性质,可以直接施加本质边界条件.同时利用Taylor展开法,建立了随机结构分析的Taylor展开随机径向基点插值无网格法(TSRPIM).数值实例表明在随机温度场分析方面随机无网格法具有明显的优势.
Taylor展开法; 随机径向基点插值无网格法; 随机温度场
0 引言
温度场问题中的很多传热现象具有随机性,导致导热体温度随机变化的因素包括边界条件、内热源存在随机性,以及导热体热物性的不确定性等.随机热传导问题主要求解的是响应的均值和均方值、自相关函数以及功率谱密度等.
随机有限元法(SFEM)和随机无网格法二者相比,前者需要对网格不断进行重构,后者只需要对节点进行处理,故人们对无网格法愈加重视.本文通过将径向基点插值无网格法和Taylor展开法相结合得到了Taylor展开随机径向基点插值无网格法.通过随机温度场分析中的数值实例说明了Taylor展开随机无网格径向基点插值无网格法精度较高,是一种耗时少、精度高、并且简便有效的方法.
1 径向基点插值无网格法(RPIM)
对于在域Ω上有定义的函数T(x),任意分布若干个节点在Ω域中和它的边界上,选取n个节点值构造近似函数这些节点值位于某一点xq的支撑域中,且
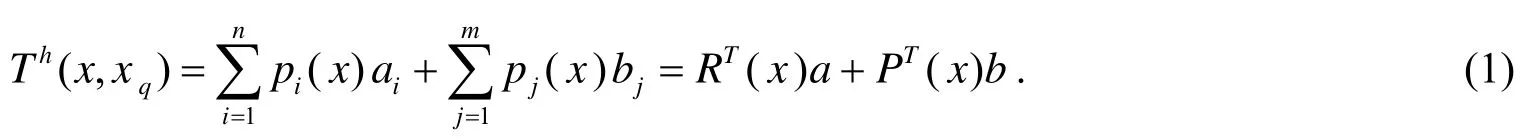
对于给定的x,有
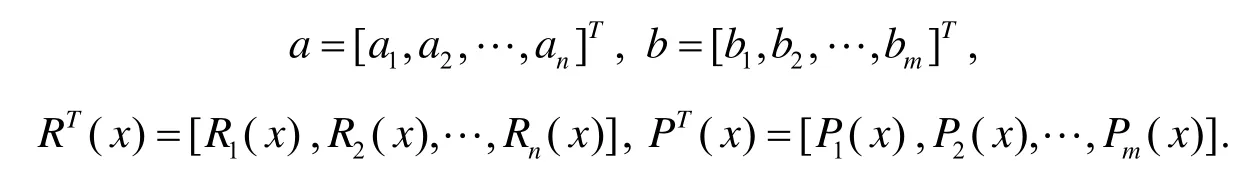
通常,在二维问题中



在方程组(2)中有n+m个未知数、n个方程,故增加m个约束方程

来进行求解.式(2)与式(3)联立可得

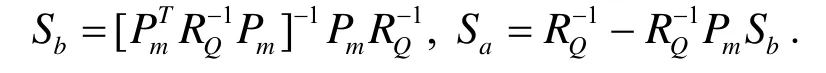
将a,b代入式(1)中,得
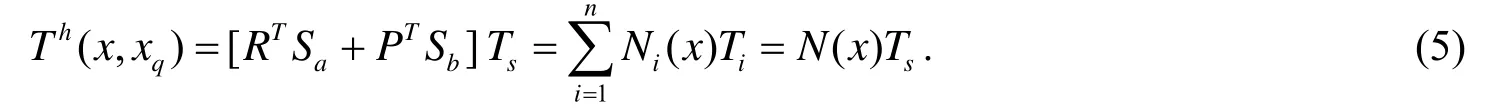
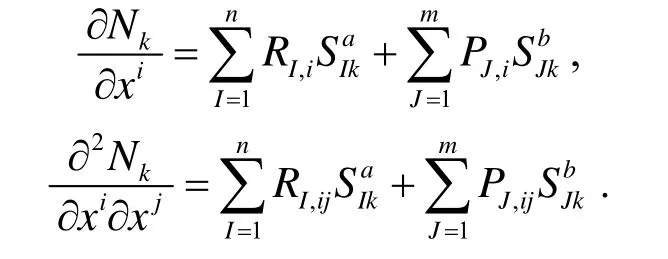
这里
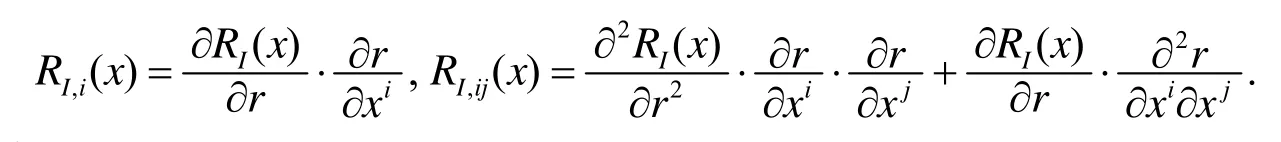
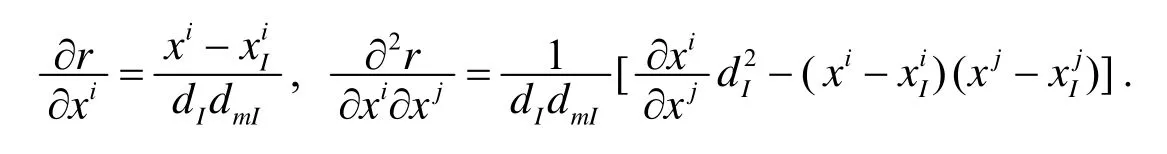
径向基函数[3]常用的形式有:
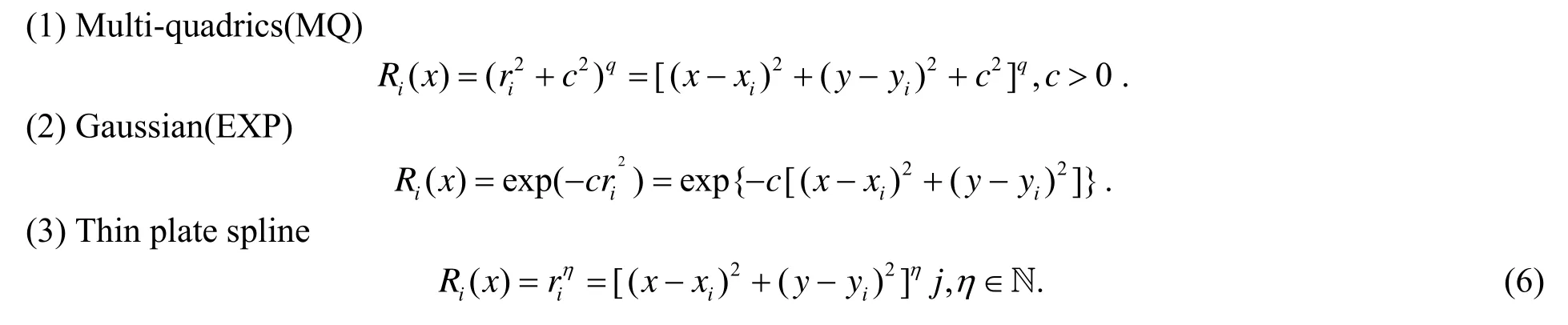

2 Taylor展开的随机径向基点插值无网格法(TSRPIM)
2.1 随机非稳态传热问题的控制方程
随机非稳态传热问题的控制方程为
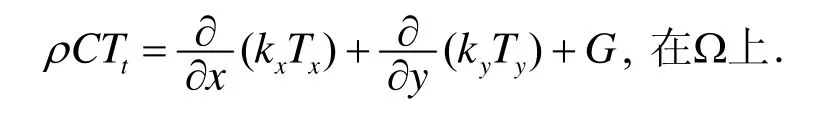
边界条件为

式(7)的等效积分形式[5]是
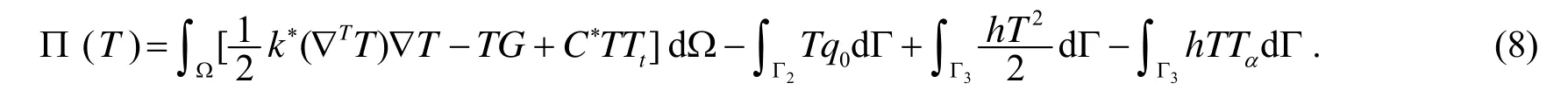
对(8)式作变分,并令其为零得
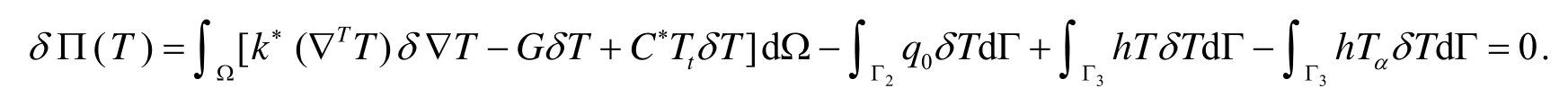
由δT的任意性,可得
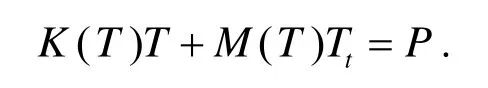
其中


上式中的 q1,q2…,qS是非稳态热传导问题中的随机变量,故T是 q1,q2…,qS的函数.
T用带有随机变量的Taylor级数展开为
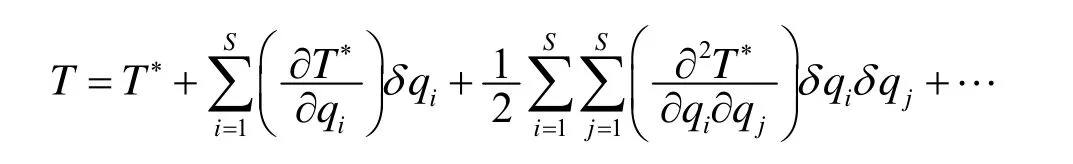

其中mn是q的第n阶矩,n是近似次数.
2.2 随机场的离散
对随机场离散的方法主要有Karhunen-Loeve展开、中心点离散法、局部平均法、形函数法[6]等.由于随机无网格法和节点、网格没有紧密联系,故这些方法对随机响应的准确性和敛散性没有关系.其中的形函数法对求解高斯积分点处的随机变量值有很重要的作用.
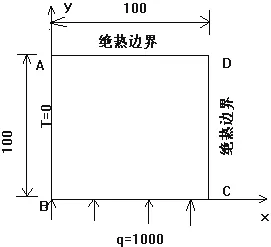
图1
3 数值算例
图1 所示的热传导问题是边长是100的正方形板,左边界AB的温度为T=0,下边界BC的热流量为q=1000,没有内热源,边界AD、CD绝热.令h为带有高斯密度分布函数的随机变量的量,该密度分布函数有平均值并满足下列条件[6,8]
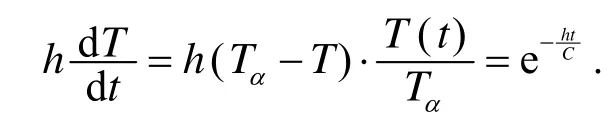
则用 TSRPIM 求解时,设置的规则节点数为676(26×26)个,高斯积分背景网格数为20×20个,各网格用4×4高斯积分,式(5)中的径向基函数取式(6)中的紧支径向基函数(TPS),多项式基取二次函数.通过用TSRPIM和SFEM进行求解,对得到的温度T的均值和方差σT随时间t的变化和精确解进行比较,结果如图2、图3所示.

图2 随时间变化的温度均值分布图

图3 随时间变化的温度方差分布图
4 结语
(1)径向基点插值有效地解决了点插值中系数矩阵奇异性问题,由于插值具有 Delta函数性质,可以直接施加本质边界条件.
(2)随机无网格径向基点插值法只需布置节点,而随机有限元法必须划分网格.
(3)一阶TSRPIM的效率在所有SRPIM中效率最高,随着随机变量的增多,二次TSRPIM的计算量非常大.一阶 TSRPIM 中逆矩阵的计算和刚度矩阵的计算次数只有一次,比摄动随机无网格径向基点插值法效率高.
(4)对随机非稳态热传导问题,应用TSRPIM 进行求解,通过MATLAB编程验证了该方法是有效可行的,比随机有限元法的精度和效率高,该方法在求解随机温度场问题中将得到很好的应用.
[1]任彦霖,李小林.Signorini 问题的无网格边界径向基点插值法[J].重庆师范大学学报(自然科学版),2015 (3): 77~82
[2]赵光明.无单元法理论与应用[M].合肥: 中国科学技术大学出版社,2010
[3]姜海南,周德亮,吴丽华.用径向基函数 Galerkin 法求两点边值问题[J].甘肃科技,2012(1): 72~73
[4]云永琥,陈建军,刘国梁,等.加权最小二乘无网格法的随机稳态温度场分析[J].华中科技大学学报(自然科学版),2015(11): 425~431
[5]王 峰,林 皋,郑保敬,等.非线性热传导问题的基于滑动Kriging插值的MLPG法[J].大连理工大学学报,2014 (5): 339~344
[6]陆传赉.工程系统中的随机过程[M].北京: 电子工业出版社,2000
[7]戴保东.改进的无网格局部边界积分方程方法研究[D].上海: 上海大学博士学位论文,2006
[8]MAGRAB E B,AZARM S,BALACHANDRAN B,et al.MATLAB原理与工程应用[M].第2版.高会生,李新叶,胡智奇,等译.北京: 电子工业出版社,2006
Analyzing Stochastic Unstable Heat Conduction Problems with Taylor Expansion Stochastic Meshless Radial Point Interpolation Method
ZHAO Yufeng
(Basic Teaching Department,Shanxi Technology and Business College,Taiyuan 030006,China)
The stochastic temperature field was analyzed by Taylor expansion stochastic meshless radial point interpolation(RPIM)method (TSRPIM).A radial point interpolation method which is based on the radial function is a new meshless method.Because of the interpolation function with the combination of radial and polynomial basis,it is also easy to deal with essential boundary conditions for its property of Kronecher Delta function.By the Taylor expansion method,a Taylor expansion stochastic meshless radial point interpolation method in probabilistic structural analysis was constructed.Numerical example shows that Taylor expansion meshless radial point interpolation method (SMRPIM)can be applied in probabilistic temperature field with obvious superiority.
Taylor expansion method,Taylor expansion stochastic meshless radial point interpolation method (TSRPIM),probabilistic temperature field
O241.3 文献标识码: A 文章编号: 1672-5298(2017)02-006-05
2017-01-08
赵玉凤(1985- ),女,山西太原人,硕士,山西工商学院教师.主要研究方向: 无网格法

