热传导方程的解的衰减性质研究
张鹏雷
(西北大学)
热传导方程的解的衰减性质研究
张鹏雷
(西北大学)
讨论了热传导方程的解的衰减状态估计问题,主要用两种方法说明热传导方程的解在大时间下是渐进自相似的.一种直接建立在解的表达式上;然而这种方法对非线性偏微分方程一般不适用.另一种方法通过说明重整解的函数列的收敛性,利用热传导方程结构,以解的标度变换为基础,思想可被应用在非线性问题中.
热传导方程;Gauss核;衰减估计;渐近性;标度变换
1 时间趋于无限时热传导方程的解的性质
1.1 解的衰减估计
考虑热传导方程
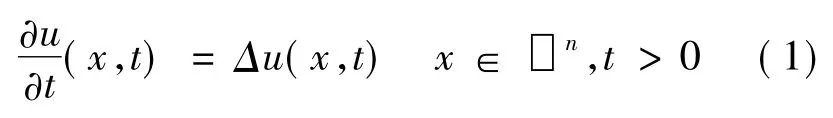
考虑解u满足(1),初始温度分布为

(3)的解可以表示为[1]


关于x1,….xn和t>0任意阶可微,满足(1).满足(2).因此u是(3)的解.
定理1.1设f在上有界且一致连续,则当t→0(t>0)时Gt*f一致收敛到f,即
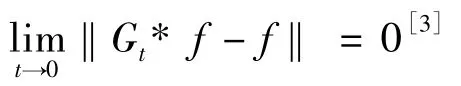
猜测当t→∞ 时,u(x,t)→0.
命题1.1设(4)是热传导方程(3)的解,则
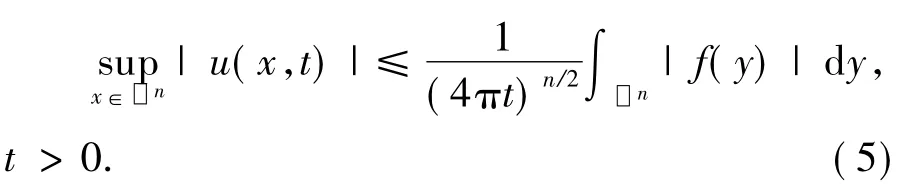
证明对于(4),t>0,有
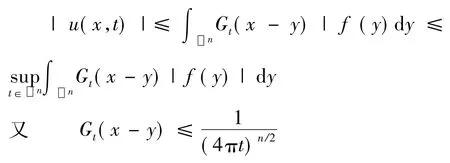

通过(5),知t→∞ 时,u至少具有t-n/2的衰减率.
下面讨论|u|的积分或它的指数次是否衰减.
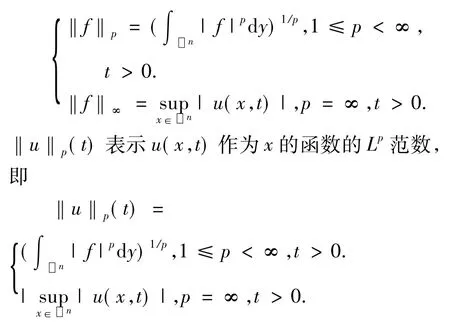
1.2 Lp-Lq估计
定理1.2设u((4)式)是热传导方程(3)以f为初值的解,1≤q≤p≤∞,则
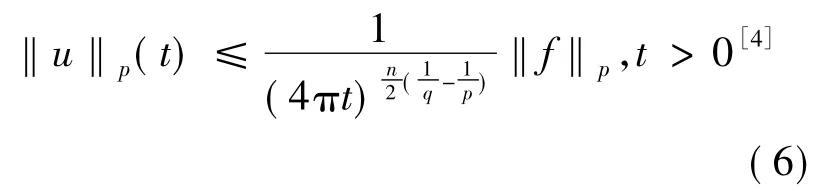
u的Lp范数的衰减率被t的小于等于0次方所估计.当p=∞,q=1时,(6)即为(5).
证 明‖u‖p(t) = ‖Gt*f‖p≤‖Gt‖r‖f‖q,t>0.

只有当q=1,p=∞ 时r=∞,(6)即为(5).
接下来讨论t→∞时u的导数是否衰减到0.
定理1.3设(4)是热传导方程(3)以f为初值的解,1≤q≤p≤∞,存在一个只取决于p,q,n的常数C=C(p,q,n)有
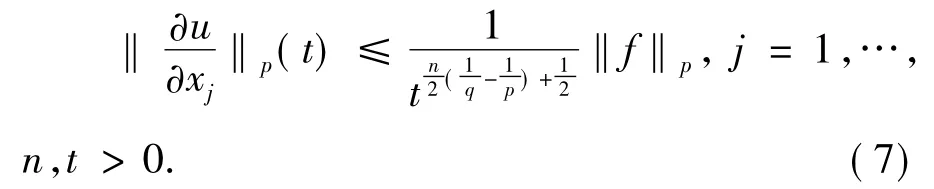
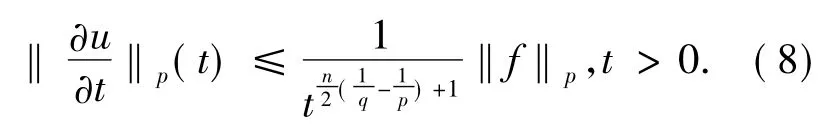
存在一个常数C=C(p,q,n,k,α)有

k是一个自然数或0,α是一个复合指数(α1,…,αn);αi(1≤i≤n)是一个自然数或0.从(7),(8)和(9)中可知对空间变量微分一次后,t的指数增加了,对时间t微分一次后,t的指数增加了1.
1.3 关于时间趋于无限时的解的性质的定理
定理4设u((4)式)是热传导方程(3)以为初值的解,则

其中g(x,t)=Gt(x).
这个定理证明当t→∞,m≠0时,u与mg有着相似性.当m=0时,(10)表示t→∞ 时,‖u‖∞(t)比t-n/2趋向于0更快.
证明
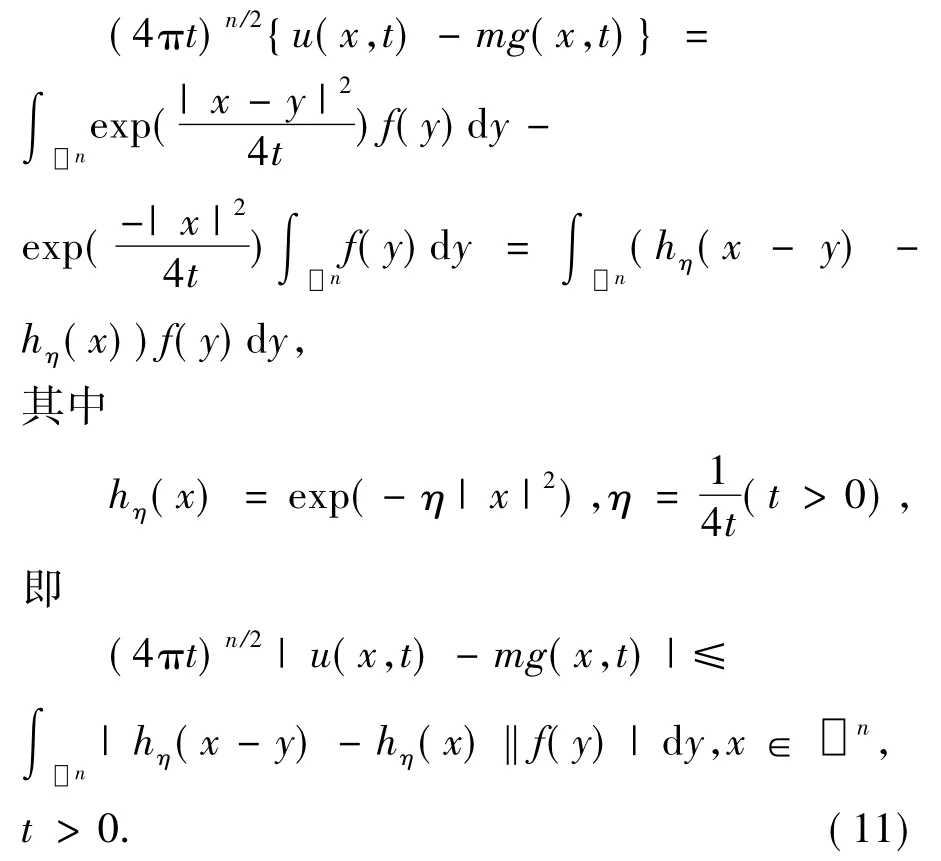
利用积分形式的中值定理,有
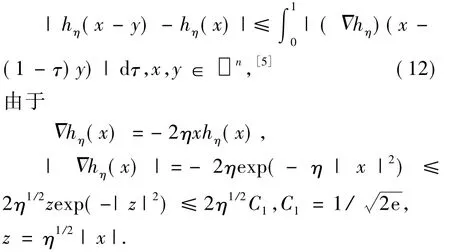
利用这个不等式及(12),有|hη(x-y)-hη(x)|≤2|y|η1/2C1.
应用到(11)中有
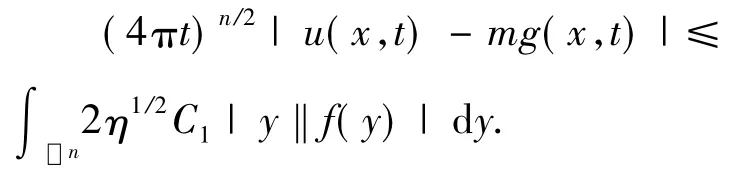
由于这个不等式的右端与x无关,两端都取上确界有

2 方程的结构和空间变量的衰减估计
对于一类非线性问题,它的解一般不能得到一个直接表达式.下面将给出一种建立在方程结构上的证明.
2.1 尺度变换下的性质和渐近公式
命题2.1设u=u(x,t)是一个实值函数,在一个开集满足热传导方程∂tu- Δu=0,即
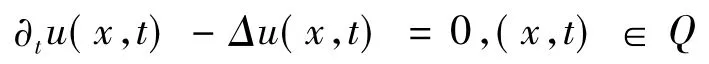
对任意的非零实数λ,定义函数
uλ(x,t)=u(λx,λ2t),则下面的性质成立
(i)函数 uλ在: (λx,λ2t)∈Q}上满足热传导方程.
(ii)对任意非零实数μ,函数μu在Q上满足热传导方程[7].
命题2.2渐近公式(10)等同于[8]

证明对于k2=t,有

从而获得了(13)和(10)的等同性.
基于这个事实,为了了解(x,t)在无穷处u的性质,有必要研究uk(x,t)在k→∞时的极限.
公式(13)等同于渐近公式(10),表明当k→∞ 时函数列{uk}收敛到自相似解mg(t= 1)[9].
2.2 空间变量的衰减估计
命题2.3u是(3)中给出的热传导方程的解,初值为,设存在一个以原点为圆心、以j0>0为半径的开球Bj0满足suppf⊂Bj0.则对η∈(0,1),有

成立.
证明通过估计解的表达式
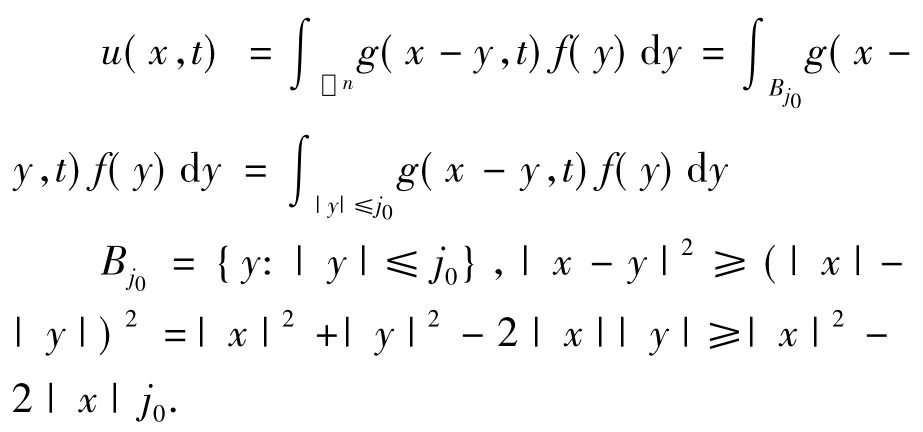
对|y|≤j0,如果η≤t≤1/η,有

3 热传导方程的解的全局Lq-L1估计


对所有的t>0和1≤q≤∞ 都成立.
当v≡0时,这种估计对应于q=1,k=4π是的热传导方程的Lp-Lq估计(5).这个估计重要的是可不依赖于k的空间函数v,如果div v= 0,即使当t→0时v发散[11].
[1]Giga M,Giga Y,Saal J.Nonlinear Partial Differential Equations[M].2010.
[2]Giga Y,Kamble T.Large time behavior of the vorticity of two dimensional viscous flow and its application to vortex formation.Comm Math Phys,117,1988:459-568.
[3]Evans L C.Partial Differential Equations[M].1998.
[4]Sverak.Partial Differential Equations[M].2010.
[5]Ockendon J,Howison S,Lacey A,et al.应用偏微分方程[M].2003.
[6]Bleecker D,Csordas G.Basic Partial Differential Equations[M].1996.
[7]邢家省,李争辉.热传导方程初值问题解的若干性质[J].北京:北京航空航天大学.
Study on the Attenuation Properties of the Solution of Heat Conduction Equation
Zhang Penglei
(Northwestern University)
In this paper,the decay state estimation of the solution of the heat conduction equation are discussed.The solution of the heat conduction equation is asymptotically self similar at large time by two methods.One is directly based on the expression of the solution;however,this method is not applicable to nonlinear partial differential equations.The other method can be applied to the nonlinear problem by describing the convergence of the function of the solution and the structure of the heat conduction equation.
Heat conduction equation;Gauss kernel;decay estimate;Asymptotic behavior;Scaling transformation
O175
:A
:1000-5617(2017)01-0025-04
(责任编辑:李家云)
2016-12-22

