激光V型谐振腔的等价腔分析法

魏 勇,范一鸣

(湖南理工学院 物理与电子学院,湖南 岳阳 414006)

激光V型谐振腔的等价腔分析法

魏 勇,范一鸣

(湖南理工学院 物理与电子学院,湖南 岳阳 414006)

为了分析激光谐振腔的稳定性,选取广泛应用的V型腔作为研究对象,将V型折叠腔等效为含有透镜的三镜直型腔(共轴球面腔),然后采用*g-参数等价腔分析法,将三镜直型腔等价为不含透镜的共轴球面腔,进而考虑激光晶体的热透镜效应,采用多元件光学谐振腔等价腔分析法推导出热透镜效应下V型腔的g′-、g′-等价空腔.该方法形象地将V型腔与共轴球面腔联系了起来,有效地体现V型谐振腔中各参量之间变化关系,通过对热透镜效应下V型腔的g′-、g′等价空腔的计算,便可对V型腔的稳定性的影响因素进行求解分析,为激光谐振腔的分析和设计提供重要参考.

V型折叠腔; 等价腔分析法; 共轴球面腔; 稳定性

V型折叠腔是一种由三面反射镜构成的谐振腔,与 F-P腔、平-凹腔等共轴球面腔相比较,具备损耗低、输出功率高和横模鉴别能力高等优点,既囊括了稳定腔和非稳腔具有的优良特性,同时又弥补了这两种腔的不足.此外,V型腔还能够很好地适应激光晶体的热透镜效应,是一种十分理想的腔型.

但上述优良特性都是以合适的参量调整为前提的.对于V型谐振腔的分析,现有的研究结果为: 采用谐振腔的图解分析,将V型腔等效为腔内含透镜的共轴球面腔,再采用腔内热动力分析和模像理论[1],虽能得到一个较为精确的腔内光模特性与晶体热效应之间的关系,但难以将谐振腔具体的参量如: 腔长、折叠角和曲率半径等联系起来,且相应的参量调整十分复杂.此外,针对于腔内含透镜的共轴球面腔,虽有很多等价分析理论,如:参数等价、g′-参数等价和G-参数等价[2],但都只是针对于F-P腔或平-凹腔等共轴球面腔,并没有与V型腔或复合腔等其他腔型联系起来.因此,找到一种能够简单直观地体现V型谐振腔内各参量与谐振腔稳定性和输出特性变化关系的分析方式就显得十分关键.

本文在 V型谐振腔图解分析的基础上,结合多元件光学谐振腔的等价腔分析法,对激光晶体产生热透镜效应的V型腔进行再次等效,虽引入了像散等误差,但有效地将V型腔的各参量联系了起来,参量之间的关系与共轴球面腔中的参量关系相类似,且简单明了.通过类似的计算便可解得谐振腔的稳定性条件、输出镜面上的光斑大小和基模远场发散角,对实际应用中激光V型谐振腔的研究分析具有重要的参考价值.

1 理想状况下V型谐振腔的等价分析

所谓理想状况是指: 在固体激光器中,不考虑激光晶体的热透镜效应.理想状况下V型谐振腔结构如图1所示.

图1中,球面折叠镜M13的曲率半径为R13,端面反射镜M11、M12的曲率半径分别为R11、R12,折叠角为θ.根据矩阵光学理论,高斯光束通过透镜时的变换矩阵与球面镜上的反射矩阵相同,因而可将折叠镜近似等效为一个焦距恒定的薄透镜[3,4],如图2所示.

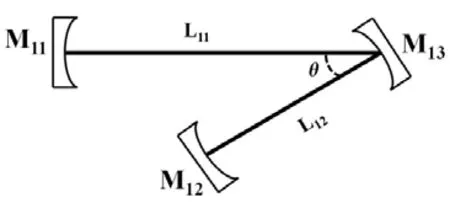
图1 V型谐振腔示意图

图2 等效V型腔示意图

上述等效方式会带来一定的像散,使子午面和弧矢面上的等效透镜焦距不一致.相应的等效透镜间距F为

对于等效后的这一类腔内含有透镜的腔型,在很多谐振腔的热透镜效应研究中十分常见,即: 将热透镜效应等效为一个焦距动态变化的薄透镜.这种腔内含有透镜的多元件光学谐振腔可以结合矩阵光学理论对其稳定性进行分析,但计算复杂且难以对输出光模特性进行求解.

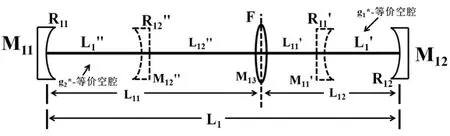
图3 V型腔等价空腔示意图

透镜将谐振腔分割为两个子腔,左侧子腔长为L11,右侧子腔长为L12,总腔长为L1.为了简化分析,仅将折叠镜等效为子午面上的薄透镜,即: 等效透镜焦距F=FT,带来的像散可通过取较小的折叠角或加入一定厚度的布儒斯特片进行消除[1].

当左侧端面镜通过透镜在右侧成像时,像与右侧端面镜构成等价空腔.设像M1′1的曲率半径为R1′1,像方子腔长为L1′1,根据透镜成像原理可知:

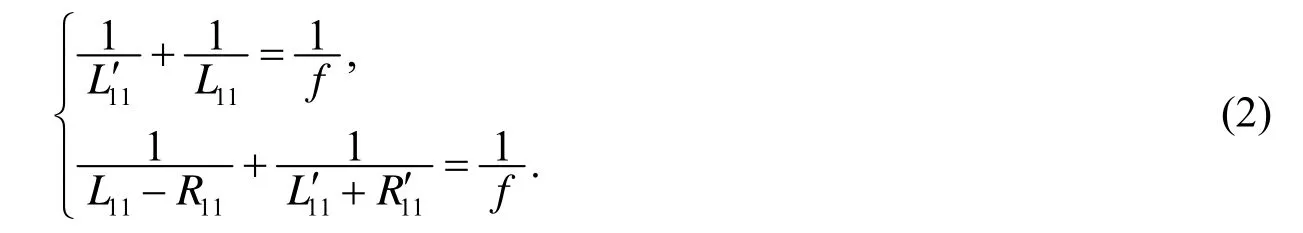
解得像的曲率半径和两子腔等效腔长为

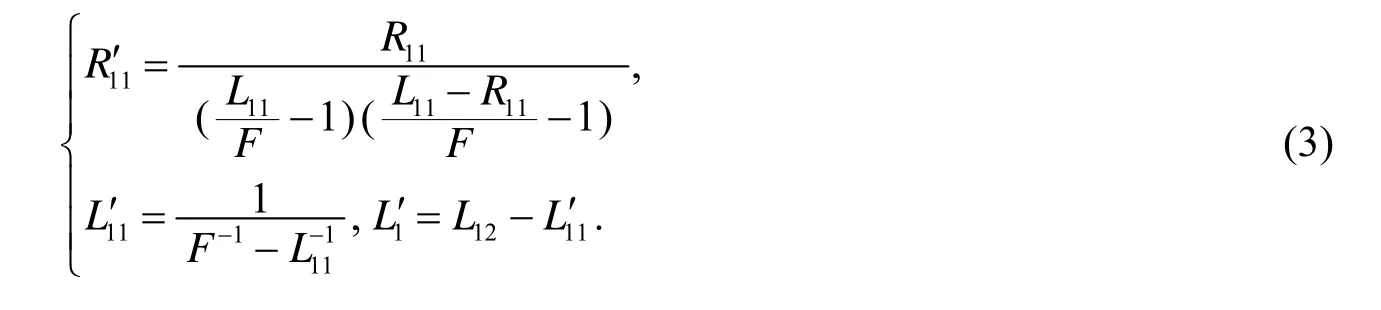
式(4)仅表示右侧子腔的稳定条件,不能用来求解左侧子腔稳定性[6].同理,如图3所示,设参数等价空腔的腔长为右端面镜M1′2的曲率半径为R1′2,则结合式(3)和(4)可解得对应的左侧子腔等效参量和稳定性条件为

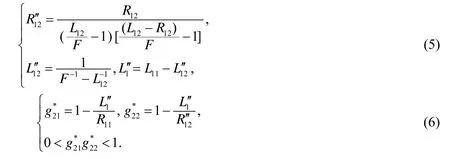
2 热效应下V型谐振腔的等价分析

上述分析忽略了固体激光器中的激光晶体,而在实际的固体激光器中,光泵浦和冷却会使激光晶体产生热透镜效应.在谐振腔热稳定性的研究中,为了简化分析往往将晶体热效应等效为焦距随泵浦功率动态变化的热透镜[8～10].

对于热效应下 V型谐振腔的分析,同样采取上述热透镜等效方式,并结合前面理想状况下的等价分析,即热效应下的等效V型腔,如图4所示.

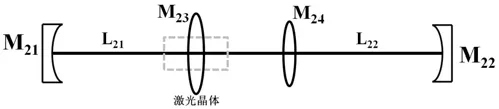
图4 热效应下的等效V型腔示意图

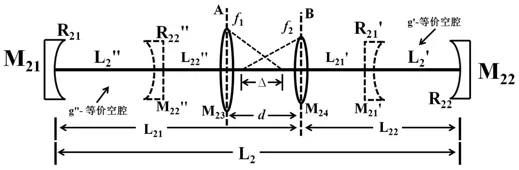
图5 热效应下V型腔等价空腔示意图

虽然腔内增加了一个热透镜,与折叠镜等效透镜形成光学透镜组,但对于这类谐振腔,同样可通过透镜成像原理进行分析.故采用多元件光学谐振腔等价腔分析法[2],即: 引入光学间隔参量 Δ,表示第一个透镜的像方焦点与第二个透镜的物方焦点之间的距离.利用牛顿公式和高斯公式依次对两透镜的成像关系进行分析,将含有透镜组的共轴球面腔按照成像原理等价为不含透镜的空腔.热效应下V型腔的g′-、g′-等价空腔如图5所示.

图5中,端面反射镜M21、M22的曲率半径分别为R21、R22,透镜M23、M24的焦距分别为 f1、f2,透镜组将谐振腔分割为两个子腔,左侧子腔腔长为L21,右侧子腔长为L22,两透镜间距为d,光学间隔为Δ.

当左侧端面镜通过透镜组在右侧成像时,其像与右侧端面镜构成等价共轴球面空腔,如图5所示,设像M2′1的曲率半径为R2′1,像方子腔长为L2′1,根据光学系统成像原理可解得曲率半径R2′1和等价空腔的腔长 L2′为

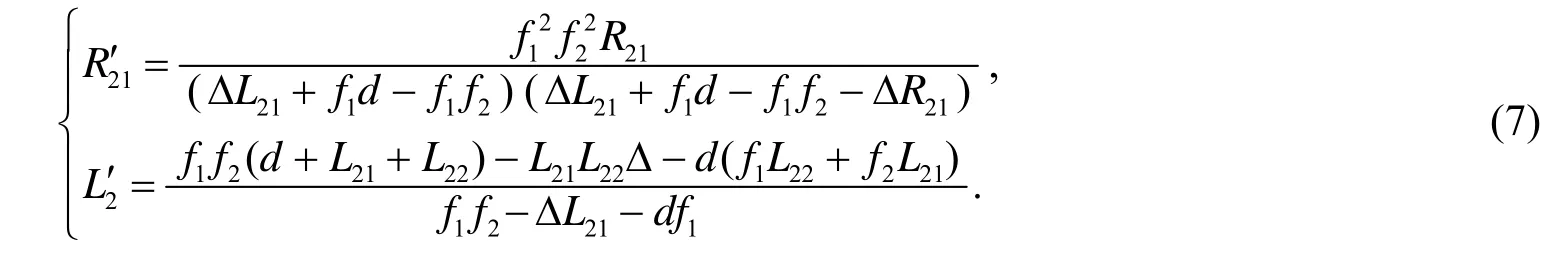
当满足条件(8)时,图5所示B线往右的子腔稳定,但不能表示A线往左的子腔稳定性.对应的左侧子腔等效参量和稳定性条件可按照相同的透镜组成像原理进行求解,如图5所示,设g′-参数等价腔的腔长为 L2′,右端面镜 M3′′2的曲率半径为 R2′′2,解得

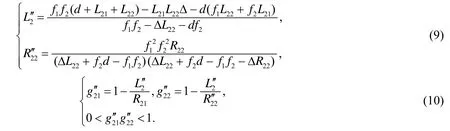
考虑到激光器工作时的热透镜效应,V型谐振腔的稳定性求解直接转化为谐振腔的等效g′-、g′-参量求解.将式(7)、(9)分别代入式(8)、(10),可以通过软件仿真依次分析腔的结构参量(如两侧端面镜曲率半径、折叠镜曲率半径、折叠角、等效透镜间距和总腔长以及激光晶体在腔中的位置等)对V型腔稳定性的影响,从而设计出具有较宽热稳定范围的激光谐振腔.

3 结论

为了分析激光谐振腔的稳定性,本文选取广泛应用的V型腔作为研究对象,将V型折叠腔等效为含有透镜的三镜直型腔(共轴球面腔),然后采用*g-参数等价腔分析法,将三镜直型腔等价为不含透镜的共轴球面腔,进而考虑激光晶体的热透镜效应,采用多元件光学谐振腔等价腔分析法推导出热透镜效应下V型腔的g′-、g′-等价空腔.对于激光器工作在理想状况或热效应状态下,V型谐振腔的稳定性求解直接转化为谐振腔的等效 -参量求解.而 -参量又是衡量等效V型腔稳定性的关键因素,并直接由V型谐振腔的各参量决定.一旦V型谐振腔的某一参量(如两侧端面镜曲率半径、折叠镜曲率半径、折叠角、等效透镜间距和总腔长等)发生变化,必然引起谐振腔的稳定性发生相应变化.该方法将 V型折叠腔的分析有效地与共轴球面腔的分析理论联系了起来,对激光谐振腔的分析和设计能够提供参考.

[1]李 锋,白 杨,白晋涛,等.一种V型固体激光腔的热动力图解分析[J].延边大学学报: 自然科学版,2006,32(3): 176～180

[2]吕百达,魏光辉.多元件光学谐振腔的等价腔分析法[J].四川大学学报: 自然科学版,1985,(4): 48～55

[3]万大平,王裕民,归振兴,等.一种激光折叠腔稳定性分析及设计的新方法[J].中国激光,2007,34(9): 1217-1221

[4]SHAN X Y,WEI X Y,NIAN-LE W U,et al.Study on the beam quality of diode pumped Yb:YAG thin disk laser and the intracavity frequency doubling in V-type resonator [J].Chinese Journal of Quantum Electronics,2004

[5]KOGELNIK H.Imaging of optical modes — resonators with internal lenses [J].Bell Labs Technical Journal,1965,44(3): 455～494

[6]曹 清,张为俊.多元件谐振腔的等价腔[J].光学学报,1994,14(2): 135～139

[7]周炳琨.激光原理[M].第7版.北京: 国防工业出版社,2014

[8]吴 羽,龙晓莉,焦中兴,等.热透镜效应补偿的高功率Nd: YAG激光器的优化设计[J].激光技术,2015,39(3): 377～380

[9]余本海,倪永军,娄国营.Nd: YAG激光器的热透镜效应及其对激光输出的影响[J].信阳师范学院学报: 自然科学版,2004,17(2): 166～169

[10]MAGNI V.Resonators for solid-state lasers with large-volume fundamental mode and high alignment stability [J].Applied Optics,1986,25(1): 107

Equivalent Cavity Analysis of Laser V-type Resonant Cavity

WEI Yong,FAN Yiming
(College of Physics and Electronics,Hunan Institute of Science and Technology,Yueyang 414006,China)

In order to analyze the stability of laser resonator,the widely used V cavity is chosen as the research object.The V cavity is equivalent to a “three mirror cavity” with a lens in the cavity (coaxial spherical cavity).Then,using the*g- parameter equivalent cavity analysis method,the three mirror cavity is equivalent to the coaxial sphere without lens.Considering the thermal lens effect of laser crystal,the equivalent cavity of g′- and g′- cavity in V cavity with thermal lens effect was deduced by using equivalent cavity analysis method of multi element optical resonator.The V cavity and the coaxial spherical cavity are effectively connected.and the relationship between the parameters of V resonator is effectively reflected.Based on the calculation of the equivalent cavity of g′- and g′- in the V cavity under the thermal lens effect,the stability of the V cavity can be solved.It can provide important reference for the analysis and design of laser resonator.

V-type folded cavity,equivalent cavity analysis,coaxial spherical cavity,stability

TN242 文献标识码: A 文章编号: 1672-5298(2017)02-0023-04

2017-03-28

国家重大科研仪器研制项目(21427801); 湖南省教育厅优秀青年项目(17B112)

魏 勇(1977- ),男,湖南岳阳人,湖南理工学院物理与电子学院副教授.主要研究方向: 激光与非线性光学