CFRP加固混凝土梁的非线性有限元分析
聂 琮,张红星
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590;2.山东省土木工程防震减灾重点实验室,山东 青岛 266590)
CFRP加固混凝土梁的非线性有限元分析
聂 琮1,2,张红星1
(1.山东科技大学 土木工程与建筑学院,山东 青岛 266590;2.山东省土木工程防震减灾重点实验室,山东 青岛 266590)
碳纤维复合增强材料(CFRP)具有轻质、高强等特点,在我国混凝土结构加固中得到了广泛的应用.本文基于有限元软件ANSYS,对材料本构关系的选取、有限元模型的建立、网格划分、二次受力的实现及混凝土与CFRP之间的粘结滑移处理方式进行了探讨.以9根试验梁作为依据,将试验结果与数值模拟结果进行对比分析.结果表明,数值模拟结果与试验结果基本一致,所建立的有限元模型能较好地反应真实状况; 且利用ANSYS可以较好地模拟CFRP加固梁在承载过程中的荷载效应,为实际工程提供了参考.
有限元; 碳纤维复合增强材料(CFRP); 非线性; 加固; 数值模拟
纤维复合增强材料(FRP)是由纤维材料与基体材料按照一定的比例混合并经过一定工艺复合形成的高性能新型材料[1].其中碳纤维复合增强材料(CFRP)最初应用于航天领域,后来又逐渐应用于船舶、军工、汽车等领域.近年来,因为其具有比强度高、质轻、耐腐蚀性能好、施工方便等优点广泛应用于我国的建筑结构加固中[1,2].
目前,对CFRP加固梁承载力的研究大多基于试验基础.利用有限元方法对加固结构进行分析,不仅节约了时间,而且能很好避免试验过程中数据的离散性.虽然采用数值模拟软件对CFRP加固梁进行分析已取得较为令人满意的效果,但是部分学者往往将有限元模型进行了简化,忽略了混凝土与CFRP之间的粘结滑移[3,4].其次,采用CFRP对结构进行加固时,很难实现对加固结构的完全卸载,因此也未考虑加固结构多属于二次受力结构这一特点.
1 ANSYS有限元模型建立
1.1 单元类型的选择
Solid65单元是ANSYS中专为混凝土等抗压强度远大于抗拉强度等非均质材料设置的8节点单元.该单元可以较为真实地模拟混凝土材料在受力过程中的荷载效应,其中包括塑性变形引起的材料非线性以及大位移引起的几何非线性.
对于钢筋的模拟,选取可以承受轴向拉压但不能承受弯矩的 Link180单元.通过输入 2个节点坐标,截面面积及材料属性可对该单元进行定义.
采用Shell41单元对CFRP材料进行模拟,该单元称为4节点壳(膜)单元,仅具有平面面内膜刚度但无平面外的弯曲刚度.因此,选用该单元来模拟FRP材料可承受拉应力但不能承受压应力的行为.
1.2 本构关系的选取
1)混凝土单轴受压应力应变关系的表示形式采用美国Hognestad建议的模型[5],曲线方程为

其中fc为混凝土棱柱体抗压强度;0ε为峰值应变,取为极限应变,取
2)钢筋可视为各向同性材料,采用双线性随动强化模型,屈服准则为Von Mises屈服准则.
3)由于纤维复合增强材料无明显的屈服强度,因此其应力应变关系视为理想弹塑型,即当应力达到其极限强度时被拉断.
1.3 混凝土的破坏准则
ANSYS中混凝土的破坏准则为修正的Willam-Warnke五参数模型,多轴应力状态下混凝土的失效准则表示如下:

其中F为主应力的函数; S为失效面; fc表示混凝土的单轴抗压强度.
根据文[6]建议,张开裂缝剪力传递系数取 0.5,闭合裂缝剪力传递系数取 0.95; 并且关闭混凝土压碎选项(有助于收敛).
1.4 二次受力的实现
在实际进行加固的结构中,往往难以实现加固前完全卸载,原结构在加固前已经处于受力状态,因此加固的结构通常为二次受力结构.
求解过程中分为两个荷载步来模拟二次受力.第一个荷载步中使用 Ekill命令“杀死”纤维布单元,即将其刚度矩阵乘以一个很小的因子,忽略其对整体刚度矩阵的贡献; 在第二个荷载步中使用Ealive命令激活已“杀死”的纤维布单元,使其刚度达到真实状况.
1.5 混凝土与CFRP之间的界面处理
混凝土与CFRP之间的胶层,是二者共同工作的基础.对于连接混凝土与CFRP之间的胶层的处理方式,主要有耦合节点[7]、采用节理元[8]、采用接触单元[9]、采用弹簧单元[10]等四种情况.耦合节点法是使混凝土单元与纤维布单元共用节点,忽略二者之间的相对滑移,使其达到共同工作的效果; 采用接触单元即把混凝土底面作为刚性接触面,把纤维布顶面作为柔性目标面.这两种模型与真实情况都有一定差距.
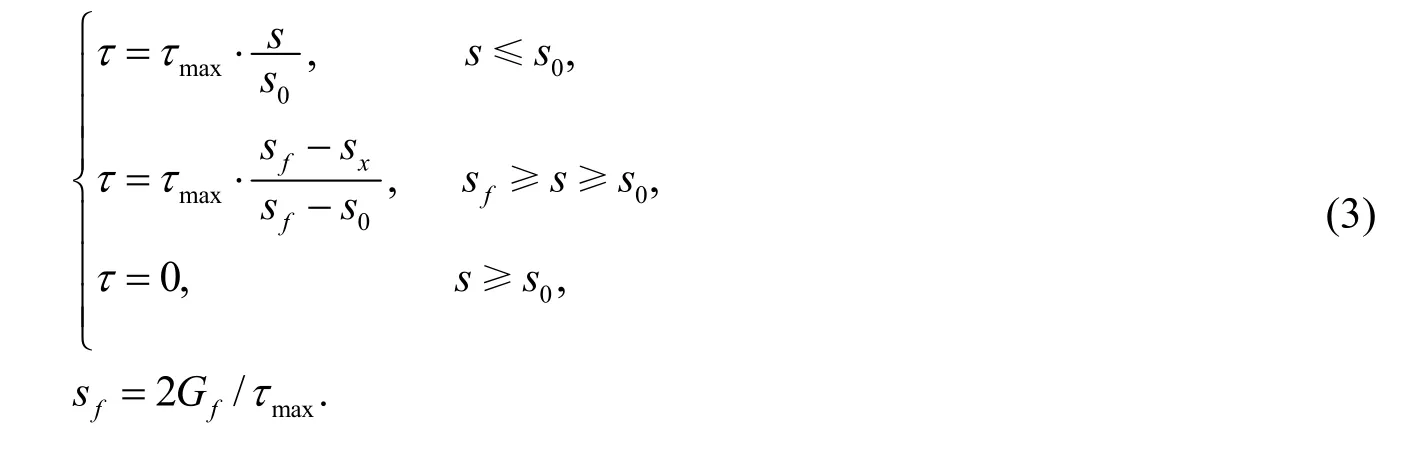
其中τmax为黏结应力—滑移曲线的最大剪应力; s为滑移量; s0为粘结应力达到τmax时滑移量; Gf为截面破坏能,与FRP-混凝土宽度系数及混凝土抗拉强度有关。
本文采用非线性弹簧单元Combin39模拟连接混凝土与纤维布之间的黏结滑移,即沿着平行于界面长度方向(x方向)的重合节点处布置单向弹簧单元,并耦合重合节点垂直于界面长度方向(y方向)的自由度.弹簧单元示意图,如图1所示.将公式(3)中的τ乘以纤维布的面积即可得到界面的粘结力—滑移关系,把得到的关系式输入Combin39单元的F-D曲线中即可完成对弹簧单元的定义.

图1 弹簧单元示意图
2 加载与求解
2.1 加载及网格划分
求解过程中,为了防止在支座处与加载点处发生应力集中现象,分别在上述两点设置刚性垫块.混凝土单元尺寸过大会影响求解精度; 而单元尺寸过小则会产生应力集中现象导致单元畸变退出计算,因此将混凝土单元尺寸控制在30~50mm之间.同时,为激活大变形选项必须将CFRP划分为三角形单元,单元边长与混凝土单元边长保持一致.
2.2 求解
求解过程中为获得较高精度,分为300个荷载子步进行加载,打开自动时间步长.收敛准则采用残余力的L2范数准则,收敛容限为0.05,迭代次数为50次,以CFRP达到抗拉强度或迭代次数超过50次而不收敛时对应的荷载为极限荷载.
3 算例及对比分析
3.1 试件编号及尺寸
本文采取文[12]及文[13]试验结果作为依据,基于前文分析建立有限元模型(图 2)并进行求解.文[12]研究了不同纤维布层数对加固梁承载力的影响,加载方式为三分点对称加载,梁截面尺寸为 100×200mm,跨度为 2200mm.文[13]研究了碳纤维布对加固已承受荷载的钢筋混凝土梁的影响,梁截面尺寸为 150×250mm,跨度为 2700mm.试验梁的编号及加固方式,见表 1.各材料的性能参数及强度指标均选取试验中的实测值,其中混凝土单轴抗拉强度采用我国规范中建议的计算式[14]

其中fcu为混凝土立方体抗压强度.
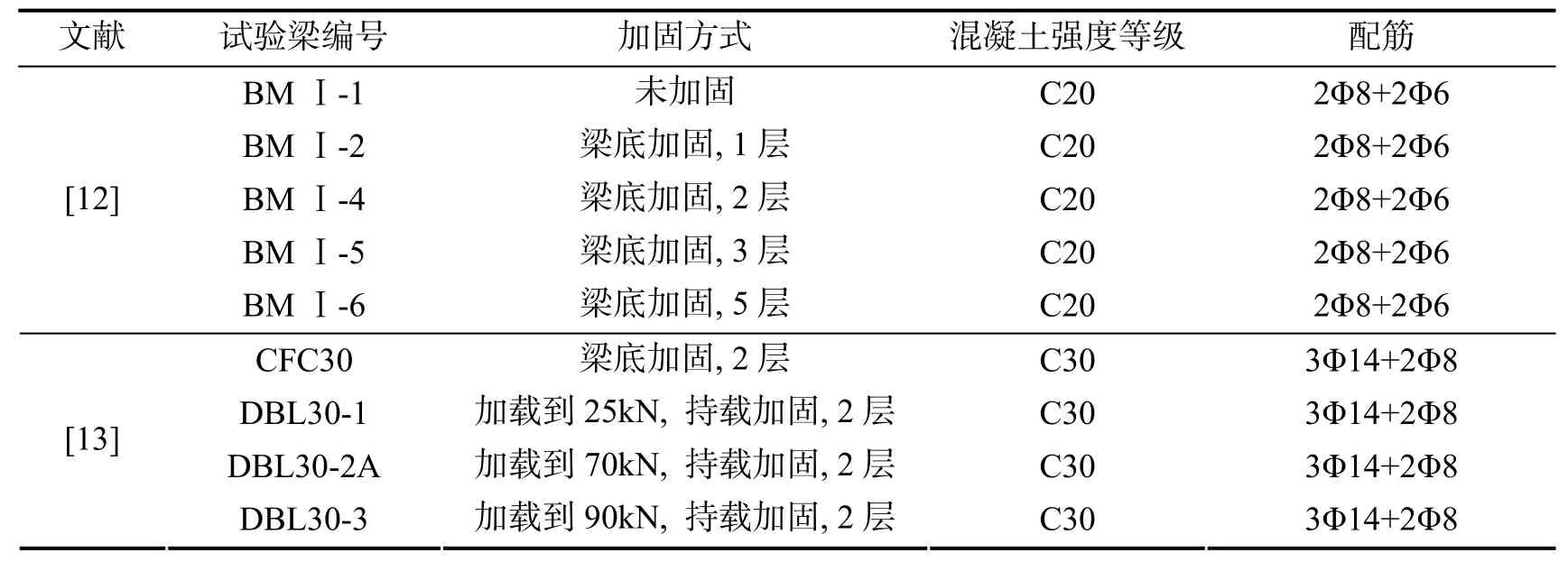
表1 梁的编号及加固方式
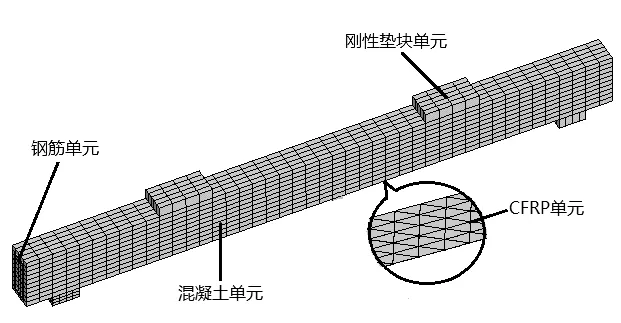
图2 有限元模型示意图
3.2 承载力对比
有限元模拟结果与试验结果的对比,分别见图3、图4.由图3与图4可知,随着纤维布层数的增多,加固梁的屈服荷载以及极限承载能力都得到明显的提高.对于一次受力构件而言,当粘贴纤维布层数较少时,数值模拟结果与试验结果较为接近,误差在10%以内; 并且通过有限元分析得到的加固梁的极限承载能力要略小于试验结果,这表明有限元分析的取值偏于“保守”,符合实际工程安全的需要.导致上述情况的主要原因是: (1)ANSYS中混凝土的应力应变关系是拉压相等的,尽管混凝土受拉段非常短,但还是对承载能力的计算有一定影响; (2)钢筋的本构模型选用的是理想弹塑性模型,未考虑钢筋的应力强化效应,导致有限元分析结果偏低.
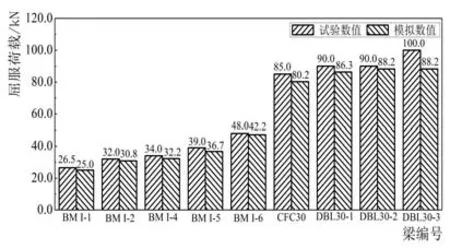
图3 屈服荷载对比
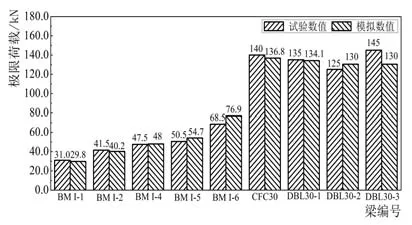
图4 极限荷载对比
实际试验过程中,当粘贴纤维布层数较多(≥3)时,界面的质量不能充分保证且构件的整体性较差,导致各层纤维布的工作效率不能得到充分发挥,因此加固梁的极限承载能力与粘贴纤维布的层数之间不是简单的线性关系.对于粘贴5层纤维布的BMI-6,其极限承载力为68.5kN,而有限元分析结果达到76.9kN,两者误差达12.3%,此时数值模拟结果要大于试验结果,即一定程度上高估了梁的承载力.
3.3 挠度对比
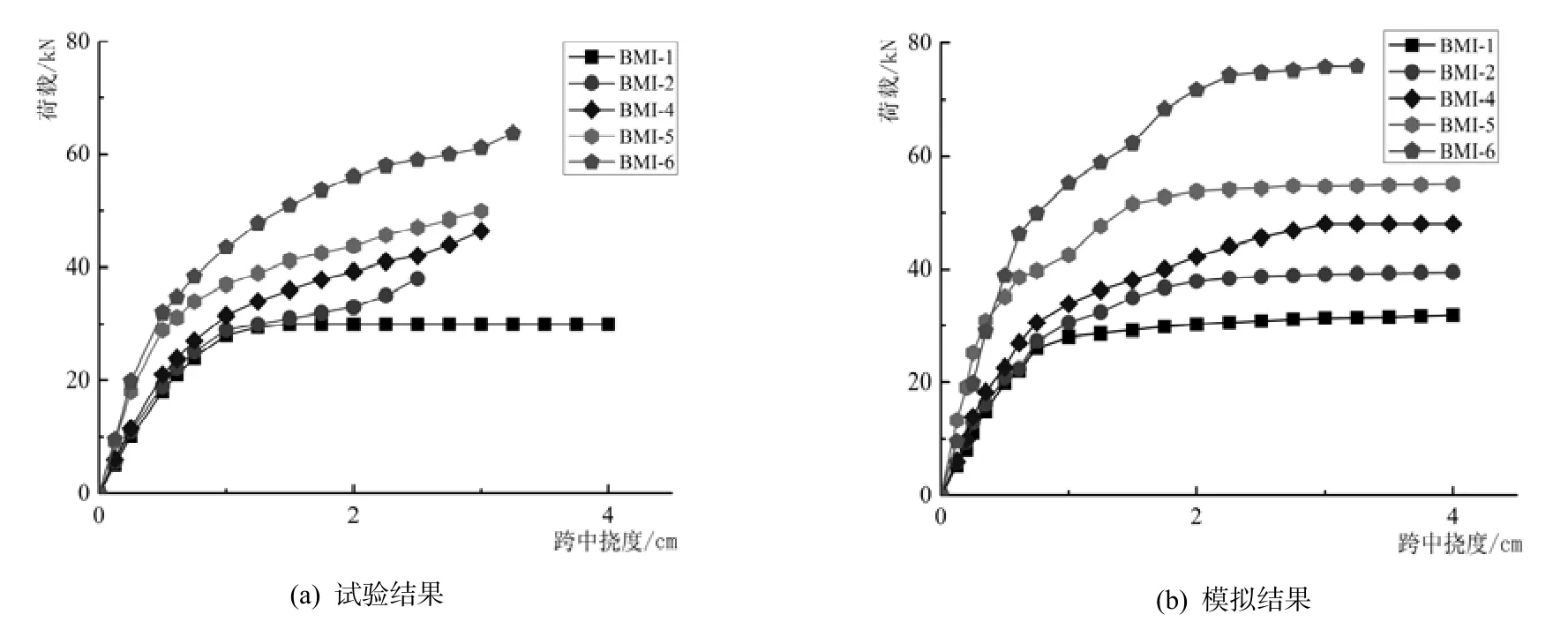
图5 跨中荷载-挠度曲线
由图 5(b)可知,当荷载相同时,随着 CFRP层数的增加,梁跨中挠度逐渐减小.当达到屈服荷载时,BMI-1的跨中挠度为5.82mm,BMI-6则为5.41mm.有限元分析结果表明,粘贴纤维布会使梁的刚度有所增加.对比图5(a)与图5(b)可知: 混凝土开裂前,有限元分析与试验数据曲线基本保持一致; 随着钢筋应力的不断增加,二者曲线呈现出微小偏差但基本呈平行关系.梁达到极限承载状态时,有限元分析得到的梁跨中挠度要略小于试验值.两者呈现微小偏差首先是因为在求解过程中未考虑混凝土的压碎;其次,通过耦合节点的方式使混凝土单元和钢筋单元共用节点,忽略了二者的相对滑移; 另外,实际试验中梁可能存在微裂缝,而有限元分析过程中忽略了微裂缝的存在,模型理想化程度较高,导致梁刚度取值偏大.
3.4 CFRP应力及应变分析
在后处理中,根据不同时间步的结果,绘制梁CFC30开裂前后底部的CFRP应力云图,如图6所示.

图6 梁底部CFRP应力分布云图
可以看到: 在梁底部混凝土未发生开裂前,CFRP的应力水平较低,最大应力位于跨中,达49.53MPa,应力从跨中沿梁长度方向逐渐递减,且沿宽度方向分布均匀.梁开裂后的瞬间,CFRP应力迅速增加,跨中的应力由49.53MPa迅速达到了187MPa,CFRP开始发挥作用; 此时CFRP应力不再沿梁长均匀变化,而是在跨中与加载点处的应力较大.随着加载过程的持续,CFRP的应力在跨中处达到最大值.有限元分析得到的梁CFC30沿纵向CFRP应力分布,如图7所示.由图 7可知,CFRP应力大幅度增长主要分为两次: 第一次迅速增长是从24KN加载到36KN时,即混凝土开裂前后; 第二次迅速增至是由72KN加载到96KN时,即钢筋屈服前后.
图 8为有限元分析得到的不同材料应变随加载过程的变化曲线.由图8可以看出: 当加载到屈服荷载时,钢筋的应变约为2000με,跨中 CFRP应力约 2100MPa.当梁达到极限承载力时,跨中的CFRP应力接近3000MPa,已经达到了极限抗拉强度; 此时受压区混凝土的压应变达 1787με,尚未达到其极限压应变,这与试验中纤维布被拉断的破坏形式相一致.
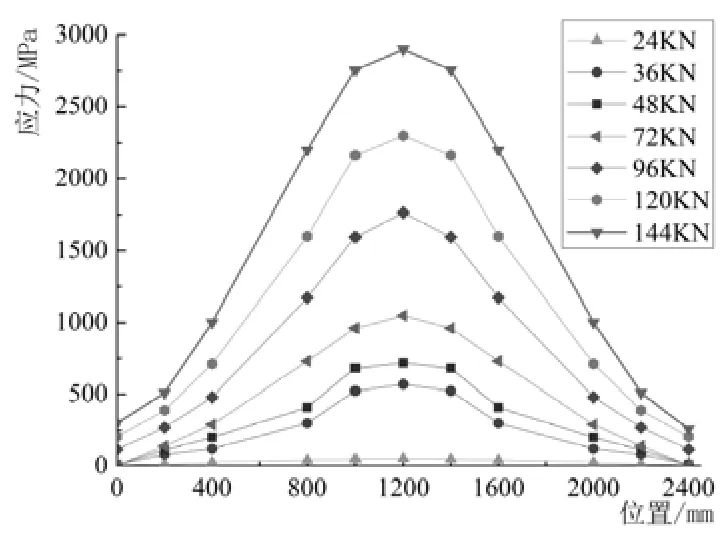
图7 加固梁(CFC30)沿纵向CFRP应力分布

图8 荷载-纵向应变
对于二次受力构件(DBL30-1/2A/3)而言,由图8可以看出当加载到25kN,粘贴CFRP时,CFRP的应变明显滞后于钢筋的应变.钢筋屈服前,两者荷载—纵向应变曲线基本平行; 当钢筋达到屈服强度后,CFRP的应变快速增加,此时CFRP的作用得到充分发挥,其应变值最终超过了钢筋.因此,有限元分析结果也再次表明,钢筋屈服前,何时粘贴CFRP对梁的加固影响效果不大,当钢筋屈服后,CFRP的加固作用才得以充分体现,因此梁DBL30-1与梁DBL30-2A的极限承载能力相差不大.
4 结论
(1)在求解过程中,网格划分及荷载子步的确定都会影响求解是否收敛.同时,是否开启大变形选项是影响求解结果能否收敛的关键.
(2)当加固层数小于等于 3层时,利用有限元软件 Ansys可以较好地分析加载过程中的荷载效应(应力、应变等)及极限承载力,且有限元分析的取值相对安全; 当加固层数大于 3层时则会一定程度上高估梁的极限承载能力,但仍在可接受的程度范围之内.
(3)有限元分析的结果也再次表明,在加载初期,纤维布应变很小,相当于起到增强钢筋的作用.随着受拉区混凝土开裂,拉应力将由纤维材料与受拉钢筋逐步承担,此时纤维材料逐步开始发挥作用; 当受拉钢筋达到屈服强度时,纤维材料的应变增长迅速,此时其强度得到充分利用与发挥.
(4)在模拟混凝土与 CFRP之间界面的相对滑移之时,只建立了平行于界面长度方向的切向弹簧单元.对于垂直于界面法向弹簧单元的刚度系数的确定有待进一步研究.
[1]叶列平,邓 鹏.FRP在工程结构中的应用与发展[J].土木工程学报,2006,39(3): 24~35
[2]岳清瑞.我国碳纤维(CFRP)加固修复技术研究应用现状与展望[J].工业建筑,2002,30(10): 24~26
[3]张芳芳,黄丽华.CFRP加固钢筋混凝土梁的非线性有限元分析[J].大连交通大学学报,2008,29(6): 24~29
[4]石欠欠,姜新佩.基于Ansys碳纤维加固混凝土梁的裂缝模拟分析[J].河北工程大学学报,2010,27(2): 25~29
[5]孙跃东,于述强,彭亚萍.混凝土结构设计原理[M].北京: 科学出版社,2013
[6]江见鲸,陆新征.混凝土结构有限元分析[M].北京: 清华大学出版社,2013
[7]赵志平,常建立,杨晓光,等.利用ANSYS对碳纤维布加固RC梁的非线性有限元分析[J].四川建筑科学究,2006: 32(1): 79~83
[8]王小荣.碳纤维布加固钢筋混凝土梁的数值分析[D].重庆: 重庆大学硕士学位论文,2003
[9]R.Z.Al-Rousan.Effect of CFRP Schemes on the Flexural Behavior of RC Beams Modeled by Using a Nonlinear Finite-element Analysis[J].Mechanics of Composite Materials,2015,51(4): 437~446
[10]钟 红,陈文茹.碳纤维布加固混凝土梁裂缝及界面性能模拟[J].辽宁工程技术大学学报,2014,33(1): 82~87
[11]陆新征,滕锦光,叶列平,等.FRP加固混凝土梁受弯剥离破坏的有限元分析[J].工程力学,2006,23(6): 85~92
[12]赵 彤,谢 剑,戴自强.碳纤维布加固钢筋混凝土梁的受弯承载力试验研究[J].建筑结构,2000,30(7): 12~15
[13]王文炜,赵国藩,黄承逵,等.碳纤维布加固已承受荷载的钢筋混凝土梁抗弯性能试验研究及抗弯承载力计算[J].工程力学,2004,21(4): 172~178
[14]中华人民共和国住房和城乡建设部.GB50010-2012混凝土结构设计规范[S].北京: 中国建筑工业出版社,2012
Nonlinear Finite Element Analysis of Concrete Beams Strengthened with CFRP
NIE Cong1,2,ZHANG Hongxing1
(1.College of Civil and Architecture Engineering ,Shandong University of Science and Technology,Qingdao 266590,China;2.Key Laboratory of Disaster Prevention and Reduction of Civil Engineering in Shandong Province,Qingdao 266590,China)
Due to its light weight and high strength,carbon fiber reinforced composite (CFRP)has been widely used in the reinforcement of concrete structures in China.Based on the finite element software ANSYS,the establishment of the model in the numerical simulation process,the meshing of the mesh,the determination of convergence criterion and the treatment method of bond slip between concrete beam and CFRP are discussed.Based on the above theoretical analysis,the experimental results and numerical simulation results are analyzed and compared with the 10 test beams.The results show that the numerical simulation results are basically consistent with the experimental results,and the ANSYS can better simulate the load effect of CFRP strengthened beams in the carrying process,which provides a reference for the actual project
finite element,CFRP,nonlinear,reinforce,numerical simulation
TU375.1 文献标识码: A 文章编号: 1672-5298(2017)02-0055-06
2017-03-17
聂 琮(1992 -),男,山东淄博人,山东科技大学土木工程与建筑学院研究生.主要研究方向: 混凝土结构抗震与加固

