复杂动态微环境中多成分的肿瘤生长对流扩散反应模型

黄雪玲,王振友

(广东工业大学 应用数学学院,广州 510520)

复杂动态微环境中多成分的肿瘤生长对流扩散反应模型

黄雪玲,王振友

(广东工业大学 应用数学学院,广州 510520)

主要针对可生长和坏死的肿瘤细胞,以及正常组织细胞、细胞间质等多成分之间的相互作用和演变关系进行了分析.在肿瘤细胞的迁移模型基础上,考虑了细胞外基质(ECM)的降解和基质降解酶(MDEs)的运输条件,构建了一个复杂动态微环境中的肿瘤生长对流扩散反应模型,并对此进行了仿真模拟分析.

微环境成分; 固体肿瘤生长; 质量守恒; 反应扩散方程

0 引言

随着对肿瘤认识的不断深入,人们发现肿瘤微环境和肿瘤的发生与发展密切相关.肿瘤及其微环境是一个复杂的由多种组成成分构成的动态混合物整体,其结构如图1所示,主要包括细胞成分、细胞外基质、血管网的内皮细胞和营养物等.

当肿瘤在人体内形成时,肿瘤生长可分为两个时期: 一是肿瘤停止生长并保持潜伏状态的无血管化期; 二是通过血管从人体“盗取”能量并不断发展的血管化期.在肿瘤无血管化期,由于血液和其他营养、氧气的供应以及运走其代谢产物的通道的限制,肿瘤的直径很少会超过1～2mm,此时肿瘤基本上处于休眠状态.处于休眠状态的肿瘤细胞并非静止不动,它仍然进行着活跃的代谢与分裂,只是肿瘤细胞的增殖与死亡达到平衡,使得肿瘤整体处于数量静止状态,这是群体休眠的状态,而非个体休眠状态.经过无血管化期后,肿瘤细胞分泌的血管生成因子过多,与抑制因子失衡,导致肿瘤的血管生成从而给肿瘤提供营养,使肿瘤体积得到进一步的扩大,并且肿瘤细胞可以通过血管扩散到身体的其他部位,导致肿瘤扩散,这是最糟糕的情况.

对于肿瘤的生长变化的研究不能仅仅依靠实验方法,建立数学模型并进行复杂的计算机模拟可以帮助解释实验和临床观察,并且可以给出对癌症的有效评估和治疗策略.

本文首先制定一个通用的微环境多成分的肿瘤模型.考虑把细胞种类作为流体的对流扩散方程模型[1],这涉及了可分化和已坏死肿瘤细胞与宿主细胞的具体情况.然后考虑肿瘤微环境的其他非细胞种类成分.采用肿瘤及其环境总共有N种成分的混合体的体积分数.根据基础混合物理论的基本思想,并且体积分数在研究的领域内是连续的,然后建立每种成分必须满足自身的守恒定律的方程.

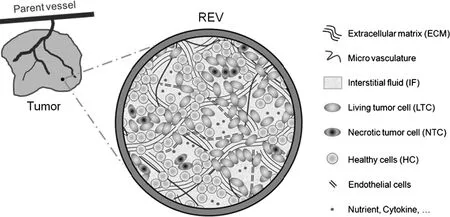
图1 单位体积的肿瘤多成分系统

1 细胞成分生长模型

考虑肿瘤及其环境构成的整体系统中的细胞成分,把整个模型的细胞分成正常的组织细胞和肿瘤细胞两个部分,并且简单地把肿瘤细胞又分为可分化的肿瘤细胞(其体积分数为φv)和已坏死的肿瘤细胞(其体积分数为φd)两类,那么整个肿瘤可表示为φT=φv+φd.

肿瘤在扩散过程中,φT在肿瘤中心处的值会很大,但是从肿瘤中心到肿瘤外处会迅速平滑趋于零,见图2(顶端).肿瘤与宿主细胞之间有一个边界面,分界面为ΣT.肿瘤体积分数介于0和1之间,如图2所示.

最常见、最方便的分界面ΣT的选择是这样可准确地确定肿瘤和宿主组织领域选用规则为

根据对流扩散反应方程[1],这三种成分都将遵循质量守恒定律,因此可以得到

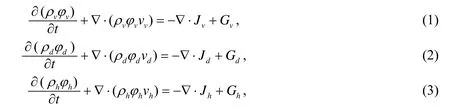
其中ρi为各种细胞成分的密度,vi为细胞运动速度、Ji为流量通量、Gi为质量改变量，φi为各种成分的体积分数.

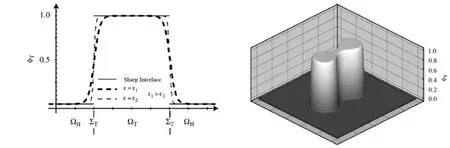
图2

由此可知,如果还知道细胞运动速度vi、流量通量Ji、质量改变量Gi和其它非细胞成分的体积分数φi,那么就可以知道肿瘤φT生长的位置和大小.

1.1 黏着能量E

为了获得细胞的速度vi和迁移流量Ji,引入一个由于各个成分之间相互作用引起的分量运动跟流量的迁移的能量Ei.这里只考虑黏附力所导致的能量Ei.

假设肿瘤细胞更倾向于黏着于其他肿瘤细胞而非宿主细胞.为了描述不同成分之间的能量,本文采用满足连续的热力学定律[1],Helmholtz自由能E=U-sθ,其中U是内能,θ是温度,是熵.本文采用Helmholtz自由能量[2],并且定义总能量为所以有第i种成分能量:

其中 是衡量分离肿瘤与宿主组织范围之间的界面扩散厚度,f是双井型能量,最小值是当和时,f可以写成两个不同形式的凸函数的组合[2]:

1.2 迁移流量J

从流量本构方程和粘附能量可以确定迁移流量.细胞的迁移流量满足再根据菲克定律[1]:

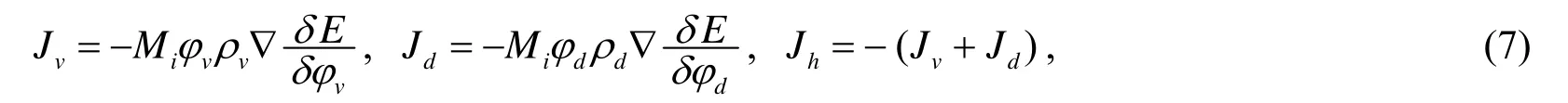
其中Mi为正常数,是一个流动系数.又由于因此有

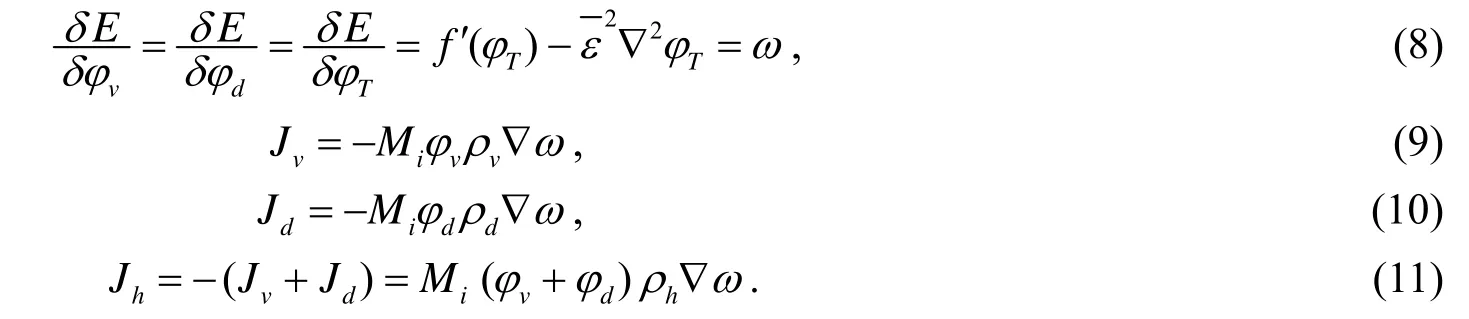
1.3 各种成分的运动速度v

由黏着能量表达式和达西定律[1],可以得到以下各种细胞的速度的表达式:

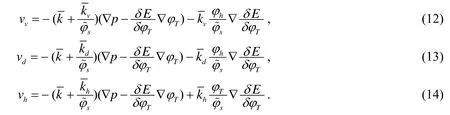
其中p表示压强.注意到这些肿瘤生长模型的迁移流量和速度的选择,是根据Ambrosi和Preziosi提出的广义动量型[1].在这些方程中,速度大小都依赖于代表由于粘附力和来自细胞与细胞的相互作用力的作用.系数分别反映细胞对压力梯度的反应.该细胞动力包含组合了细胞与细胞和细胞与间质的粘附的影响.

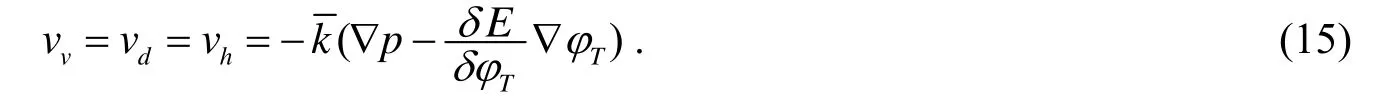
1.4 质量改变量G

如前所述,假设肿瘤细胞的坏死仅基于养分浓度n的水平,在营养低于维持细胞活动所需要的量时,就会限制肿瘤的生长.可分化肿瘤细胞的质量改变量满足[2]:

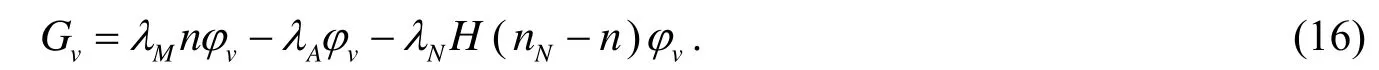
这里第一项描述的是有丝分裂,系数λM是肿瘤细胞有丝分裂率,λA表示可分化肿瘤细胞的凋亡率,λN表示可分化肿瘤细胞坏死率.

坏死细胞会经历细胞解体.当细胞发生分解时,已死的细胞会分解成水.坏死细胞的质量改变量为

其中λAφv描述了坏死肿瘤细胞的增加是由于肿瘤细胞凋亡,肿瘤细胞的凋亡率描述了坏死细胞的死亡是由于坏死率 λN≥0,H表示heaviside函数,假设可分化的肿瘤细胞的坏死是基于局部的营养浓度水平n,即当营养水平低于维持细胞生存能力的最低营养浓度nN时,则肿瘤细胞死亡,λL是坏死细胞的溶解率.

同时,还考虑了压强的影响,假设机械作用力提供反馈在细胞有丝分裂和细胞凋亡率,压力为前者提供负面反馈和为后者提供积极的反馈.因此,模型的细胞有丝分裂和细胞凋亡率依赖于压强p:

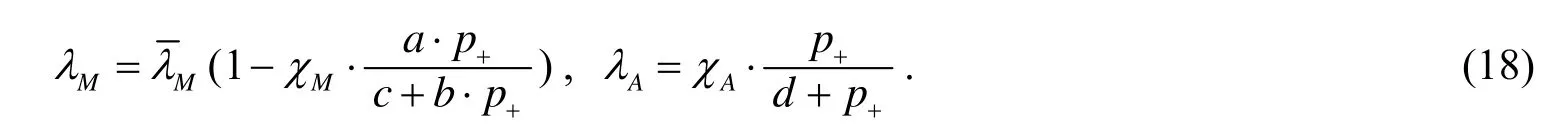
2 营养物浓度扩散

本文忽略营养物被宿主细胞的吸收量,因为跟被肿瘤细胞的吸收量比起来,宿主细胞的吸收是很少量的.利用扩散反应方程表示营养浓度的分布变化[2]:

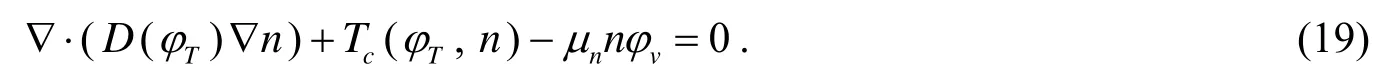
其中第1项为扩散项,D(φT)表示营养浓度的扩散系数,第2项为毛细血管内的营养物源项,第3项表示由可生长肿瘤细胞吸收了的营养.且

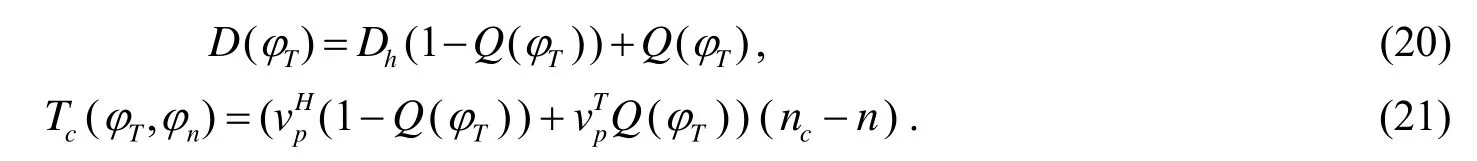
其中Dh表示正常组织中营养浓度的扩散系数,分别表示在肿瘤内和在宿主组织内营养物的传输速率,nc表示毛细血管内的营养物水平.Q()φ是插值函数,定义为

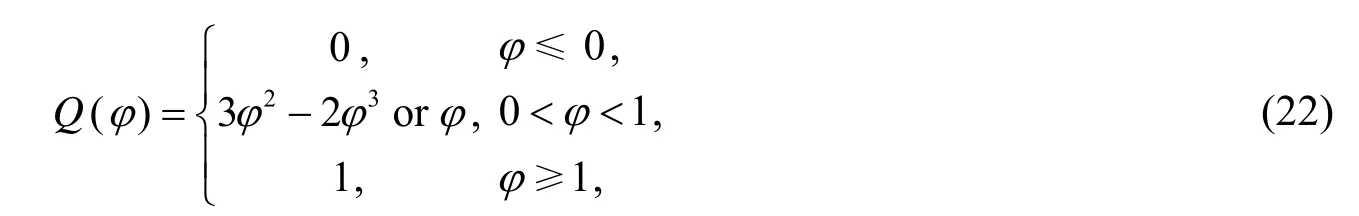
在二维的肿瘤生长模型中,由于营养浓度在肿瘤细胞与在宿主细胞的扩散程度不同,宿主细胞范围内的营养物扩散速度比较快,而在肿瘤细胞范围内的扩散取决于肿瘤细胞的数量,肿瘤细胞越多扩散越慢,故采用文[1]的其中Dh为正常组织中营养物的扩散系数,通常取1000.

3 细胞外基质

细胞是生物体基本组成单位,细胞之间存在成分复杂的细胞外基质(ECM),如图 1所示.细胞外基质ECM是由组织细胞合成并分泌到胞外、分布在细胞之间的大分子,主要是一些多糖和蛋白或蛋白聚糖,这些物质构成复杂的网架结构,支持并连接组织结构、调节组织的发生和细胞的生理活动.由于肿瘤可以通过分泌出的ECM来降解细胞外基质,从而帮助肿瘤向周围组织扩张生长.

本文引入ECM的浓度e和基质降解酶MDE的浓度m,在前人研究的基础上参考文[3],关于细胞外基质ECM的变化满足:

其中的λmE是细胞外基质的损耗率.根据文[4]MDE的浓度m满足:

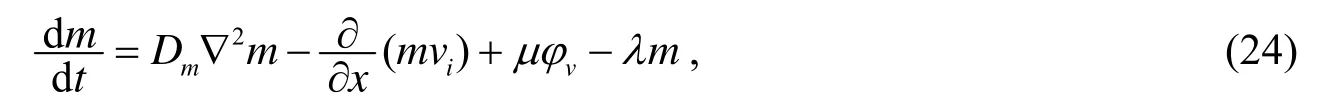
其中Dm是扩散系数,vi是宿主组织的速度,这里假设vi跟细胞组织的速度vv相同,μ是MDE的产生率,λ是MDE的衰减系数.

4 毛细血管网模型

4.1 血管内皮细胞的变化模型

血管生成的激活是肿瘤的持续生长和进展的重要进程,能够在肿瘤不断生长的过程中诱导新生血管生成,从而为肿瘤提供养分.通过求解出来的毛细血管网的内皮细胞的变化而模拟出毛细血管网,而血管内皮细胞的迁移受到由肿瘤组织释放的肿瘤血管生成因子(TAF)的控制，血管内皮细胞的趋触受细胞外基质(ECM)的浓度变化以及自身的随机运动的影响.在文[6]的基础上,进行整理得到描述内皮细胞(cec),血管内皮细胞生长因子(cVEGF),细胞外基质(e)和抗血管生成因子(cAS)的浓度分数之间满足的无量纲方程组为:

其中Dec、Dc和Db分别是内皮细胞的扩散、趋化和趋触性系数,cd,50是药物达到 50%的最大程度抑制肿瘤血管化作用的的体积分数,cd是治疗药物的体积分数,,,αr,θ,,,κ,δ,都是正的常数,c0是初始内皮细胞的体积分数,εmax是药物对内皮细胞最大的抑制作用,P(c)是一个与 VEGF的体积分数有关的“开关”函数:

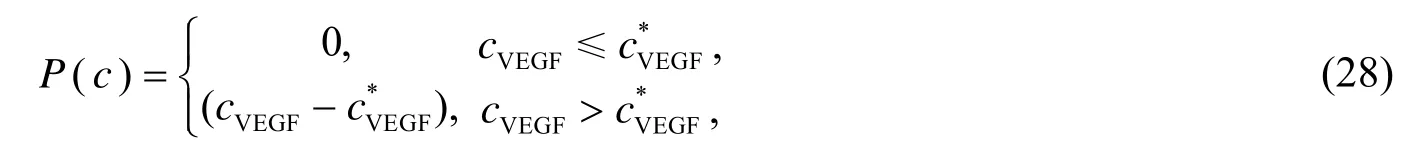
4.2 肿瘤血管芽尖分支规则

在肿瘤的血管网络的形成过程中,会发生大量的血管的分支与与融合,本文参考了孟俊萍[7]的血管分支条件,血管分支只发生在已存在的血管芽尖的位置; 只有当血管分支达到一定时间,也就是血管达到成熟的时候,同时芽尖的细胞浓度分数必须超过一定阈值时,血管芽尖才会发生分支与融合.而血管的成熟程度可用血管的生长时间来进行衡量.因此,肿瘤的血管进行的分支规则应该满足如下几个条件:

(1)当前的血管芽尖的生长时间超过阈值时间*t;

当且仅当上述条件都满足时,血管的芽尖部分才进行分支.新生的血管分支的生长时间为0,按照上述的血管内皮细胞的生长变化模型进行生长,再按照分支的规则进行分支.

(3)血管芽尖的内皮细胞体积分数大于一定阈值

5 模型的数值模拟结果及分析

5.1 模型的数值模拟结果

由于模型的方程是个复杂的高阶偏微分方程组,没办法直接求得方程组的解,所以采用离散偏微分方程的方法和选取适当量纲化的参数值进行数值求解,并且通过 matlab软件编程,对本文的肿瘤细胞的生长模型进行无量纲的数值仿真模拟.

本文的仿真模拟是在一个4mm×4mm的二维区域,均分成218×218格点中进行的.模拟的无量纲时间为t=0.01,模拟了循环了50次、100次和150次的各种成分的生长变化.肿瘤是以初始形状是位于中心椭圆型进行生长变化.

1)无血管化的肿瘤的生长模拟图

图3 肿瘤从初始形状分别经过50、100、150次循环后肿瘤的形状

2)营养物与肿瘤细胞之间的相互作用模拟图

图4 初始状态及分别经过50、100、150次循环后的营养物分布

3)ECM在肿瘤生长过程的变化模拟图

图5 初始细胞外基质浓度分布及经过50、100、150次循环后的细胞外基质分布

4)MDE在肿瘤生长过程的变化模拟图

图6 细胞外基质降解酶初始浓度分布以及分别经过50、100、150次循环后的细胞外基质降解酶分布

5)毛细血管网与肿瘤细胞的相互作用模拟图

图7 血管网与肿瘤的初始形状及分别经过50次循环后血管网与肿瘤的形状

5.2 分析与结论

如图所示,基本模拟出来肿瘤的生长,以及肿瘤向外延伸扩张生长的特点,说明本文的模型具有一定的可靠性.ECM、MDE和营养物以及微血管化对肿瘤的生长的影响如图3～7所示.刚开始,经过循环后,肿瘤会向外扩张伸张生长(图 3),肿瘤细胞开始分裂吸收周围的营养物质,使得周围的营养物由肿瘤内到外不断迅速变少,可以从营养物的变化(图4)看出,并且分泌出MDE,通过模拟出来的ECM的变化(图5和图6)可以看出,肿瘤在开始降解周围的细胞间质,从而使得肿瘤更容易向外扩张生长.从血管网的模拟图可以看出,由于肿瘤的不断扩张生长,分泌出的 VEGF(促血管生成因子)跟抗血管生成因子的失衡导致毛细血管向着肿瘤的方向生长,为肿瘤的生长提供营养成分.

本文在前人研究的基础上,各种成分都用体积分数来衡量,讨论了营养,压强,以及血管的生长在肿瘤的生长变化中变化及相互影响,并且成功地模拟出肿瘤及其它非肿瘤成分的变化图,比较系统的模拟出整个生长过程,结果与实际的肿瘤生长情况符合.

[1]Wise S M,Lowengrub J S,Frieboes H B,et al.Three-dimensional multispecies nonlinear tumor growth—I : Model and numerical method[J].Journal of Theoretical Biology,2008,253(3): 524～543

[2]Ying Chen †,Wise S M,Shenoy V B,et al.A stable scheme for a nonlinear,multiphase tumor growth model with an elastic membrane[J].International Journal for Numerical Methods in Biomedical Engineering,2014,30(7): 726～754

[3]Ying C,Lowengrub J S.Tumor growth in complex,evolving microenvironmental geometries: A diffuse domain approach[J].Journal of Theoretical Biology,2014,361:14～30

[4]NING ZHAO,KEIJI IRAMINA,XIAN CHEN.A 3d coupled mathematical model for the growth of avascular solid tumor[J].Journal of Mechanics in Medicine & Biology,2015,15(3)

[5]Zhan W,Gedroyc W,Xu X Y.Mathematical modelling of drug transport and uptake in a realistic model of solid tumour[J].Protein & Peptide Letters,2014,21(11): 1146～1156

[6]蔡 彦,吴 洁,许世雄,等.Numerical simulation of inhibiting effects on solid tumour cells in anti-angiogenic therapy: application of coupled mathematical model of angiogenesis with tumour growth[J].Applied Mathematics & Mechanics,2011,32(10): 1287～1296

[7]孟俊萍.无血管肿瘤生长和肿瘤血管生成的数值模拟[D].广州: 华南理工大学硕士学位论文,2014

[8]Tang L,Al V D V,Guo D,et al.Computational modeling of 3D tumor growth and angiogenesis for chemotherapy evaluation[J].Plos One,2014,9(1):e83962

[9]Moghadam M C,Deyranlou A,Sharifi A,et al.Numerical simulation of the tumor interstitial fluid transport: Consideration of drug delivery mechanism[J].Microvascular Research,2015,101: 62～71

[10]赵改平.抗血管生成治疗肿瘤的数值模拟[D].上海: 复旦大学博士学位论文,2007

[11]Mcgillen J B,Gaffney E A,Martin N K,et al.A general reaction–diffusion model of acidity in cancer invasion[J].Journal of Mathematical Biology,2014,68(5): 1199～1224

[12]Aboaba A A,Hameed S A,Khalifa O O,et al.Graphical and mathematical modeling of tumor shape[J].International Research Journal of Medicine &Medical Sciences,2013

Convection Diffusion Reaction Model of Tumor Growth in Complex Dynamic Environment

HUANG Xueling,WANG Zhenyou
(School of Applied Mathematics,Guangdong University of Technology,Guangzhou 510520,China)

We analyzed the growth and necrosis of tumor cells,interaction and evolution and the relationship between the normal tissue cells,interstitial cells and other components.Based on the model of migration of tumor cells,we considered the extracellular matrix (ECM)degradation and matrix degradation enzymes (MDEs)transport conditions and constructed a convection diffusion reaction model tumor growth in a complex dynamic microenvironment,and make simulation analysis.

microenvironmental components,solid tumor growth,mass conservation,reaction diffusion equation

O29; R730.2 文献标识码: A 文章编号: 1672-5298(2017)02-0016-07

2017-01-24

黄雪玲(1991 - ),女,广东河源人,广东工业大学应用数学学院硕士研究生.主要研究方向: 肿瘤数学模型

王振友(1979 - ),男,山东临沂人,广东工业大学应用数学学院副教授.主要研究方向: 医学统计分析，优化算法