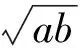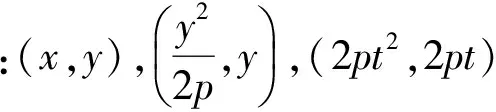例谈数学解题中的知识点、能力点与智慧点
●陈朝阳 (余杭区教育局教研室,浙江 杭州 311100)
例谈数学解题中的知识点、能力点与智慧点
●陈朝阳
(余杭区教育局教研室,浙江 杭州 311100)
文章以数学问题求解的障碍点为出发点,解读数学解题中的三大关键点:充分挖掘题设信息的知识点、培育数学解题思维链中的能力点、积累数学思维过程中的智慧点.以丰富的数学教学实践案例和2016年高考数学试题求解思维链带给我们更多的联想与思考,为深化解题教学提供一种新的思路,为学生数学学习提供一个新的蓝图.
知识点;能力点;智慧点;信息挖掘;思维链
数学解题过程中常常遇到的障碍点是来自于学生对题设条件的知识点挖掘不够,解题思维链中的能力点不到位,多条求解思路时积累的智慧点不链接.为此我们通过编制数学解题思维链的方式来解读这一现象,以期破解教学难点.
1 挖掘题设信息的知识点
任何一道数学问题,必有题设前提条件,对题设条件挖掘是否达到充分(至少不遗漏),是否会运用多种手段来挖掘,以及是否具备挖掘的“物质基础”成为首要问题.
1.1 充分性
题设条件中,给定的信息量较少时,特别要对其进行充分挖掘,通过观察结构、知识联想、多角度思考使隐藏的信息呈现出来.
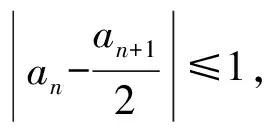
(2016年浙江省数学高考理科试题第20题第1)小题)
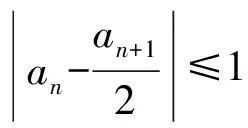
1)有绝对值结构,对它的挖掘就是绝对值三角不等式“|a|-|b|≤|a±b|≤|a|+|b|”;
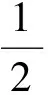
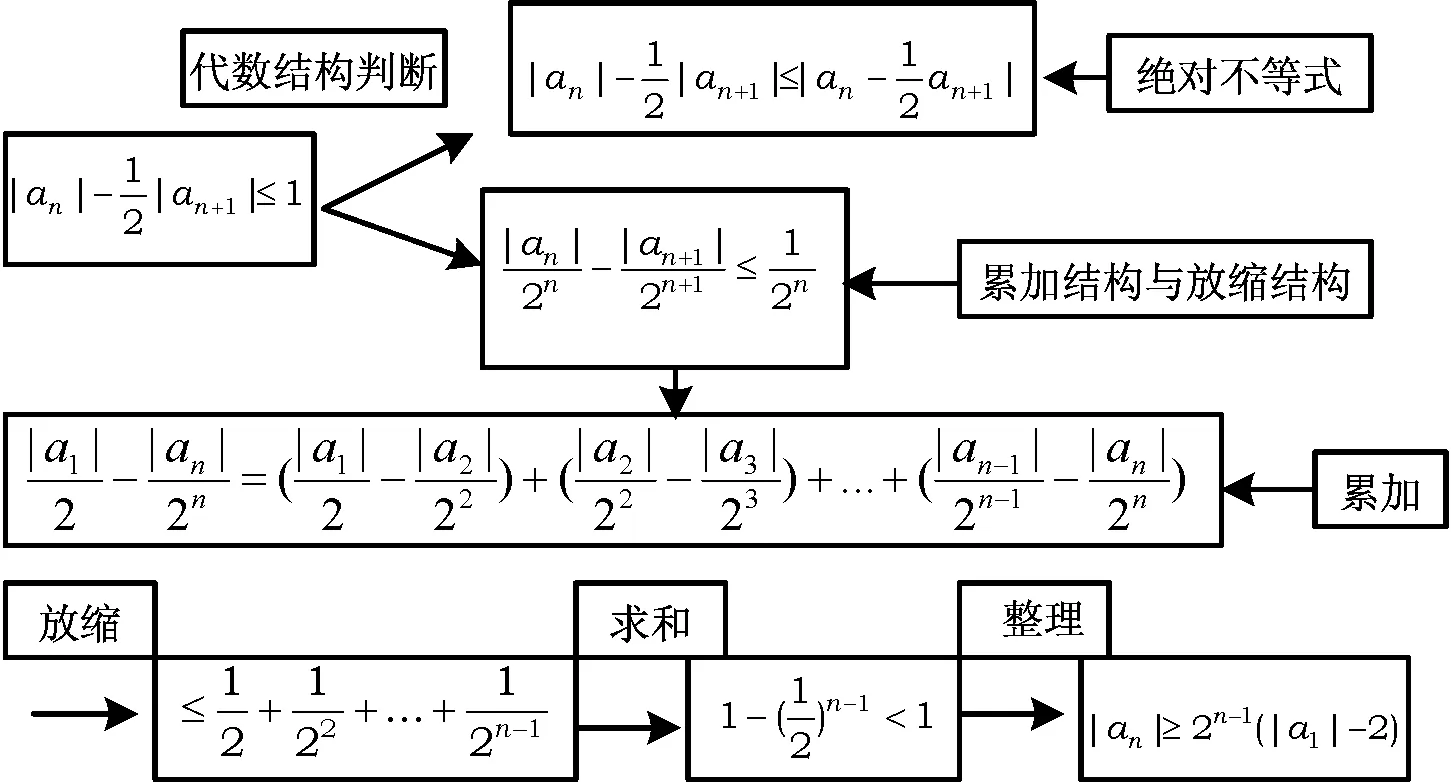
图1
此题的其他知识点都是学生比较熟悉的,题设条件中信息量非常少,只要对其结构深入挖掘,把相关的知识点都挖掘出来(如图1),题目的结构与方法就出来了,障碍也可突破了.
1.2 多样性
任何一个复杂的数学问题,信息挖掘方式要呈现多样化,既可用代数方法,也可用几何方法,甚至用实验方法等.
例2 已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8,设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(其中max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值),设H1(x)的最小值为A,H2(x)的最大值为B,求A-B.
分析 ①经配方或公式法得对称轴方程,获得二次函数f(x)的几何特征;
②经配方或公式法得对称轴方程,获得二次函数g(x)的几何特征;

④在同一个直角坐标系上绘制两个函数图像;
⑤观察两个函数图像,发现“两个二次函数图像的交点恰好是顶点”的重要特征;
⑥根据最大值、最小值函数的概念,分解确定H1(x),H2(x);
⑦计算H1(x)的最小值;
⑧计算H2(x)的最大值;
⑨计算A-B.
此例最显著的特征是“图”(如图2),对给定二次函数图像的深入挖掘,所有的信息都可以在图形中展示,所有的代数表达都在解释图中的信息,虽然这是含参的二次函数,一旦发现两函数的交汇点正是两函数的顶点时,你必定会激动与兴奋,以最快的方式触及到问题的本质!

图2
1.3 基础性
信息挖掘必须有“物质基础”——数学的基础知识(概念、定义、图像等)、基本方法(各基础知识模块中的基本方法,如数列中的递推法)、基本思想(数形结合、分类讨论、函数与方程等)以及信息挖掘的如何,可以通过罗列知识卡(图)的形式进行.

( )
A.m>n且e1e2>1 B.m>n且e1e2<1
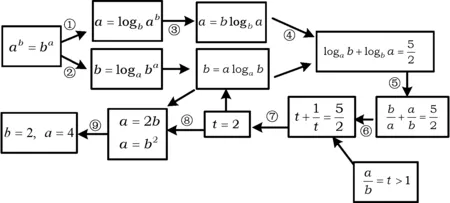
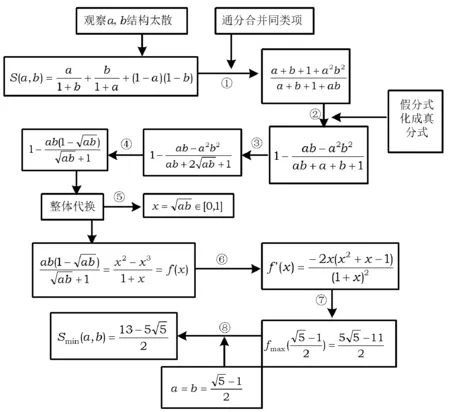
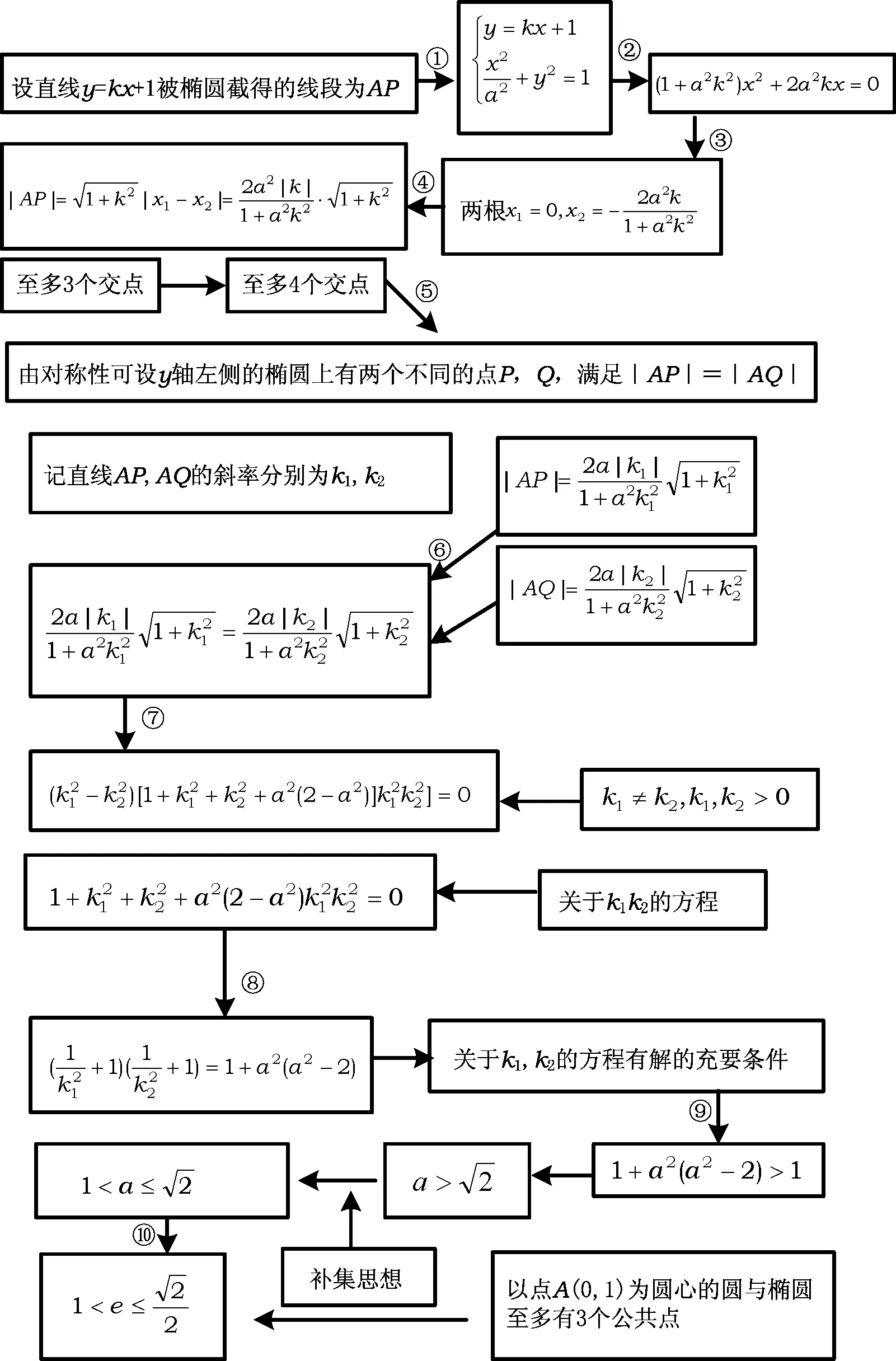
C.m (2016年浙江省数学高考理科试题第7题) 图3 分析 将解题中遇到的数学概念、公式罗列在一张图上,即将思维过程、解题过程中的数学内容展示在一张图上(如图3). 这是一个选择题,题中知识点也有如此之多,如果不能一一想到(或遇到知识点障碍),就不可能把问题的知识点链接起来,难以找到问题的答案. 2.1 判断力 2.2 联想力 2.3 运算力 正确把握运算方向、运算规则的能力,特别是代数式变形与方程求解能力.高考数学在运算速度、准确率、精细度方面的要求是必须的,进一步学习离不开它. 1)求直线y=kx+1被椭圆截得的线段长(用a,k表示); 2)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围. (2016年浙江省数学高考试题理科第19题) 此例最大的障碍点在于运算(如图4),即⑦中代数式的变形,许多考生在此被“卡”住,高考数学命题专家就要在此检验你的运算能力,此处正是目前高中生数学学习的软肋.事实上,只要按照数学运算的基本常规“有公因子,先约分,简化后续运算;遇到无理式,平方化无理为有理;遇到分式,化为整式;面对繁杂整式,先观察有无同类项,有哪些同类项可合并”等进行,都是可以越过障碍,达到成功的彼岸! 图4 3.1 敏锐性 在数学结构与运算过程中,在信息挖掘过程中,每一信息可能引伸出多个不同的新思路或新结果,能在较短时间内抓住问题本质,显示数学素养,如数感,结构感等. (2016年浙江省数学高考理科试题第12题) 快解思路 如图5所示. 图5慢解思路1 如图6所示. 慢解思路2 如图7所示. 图7 此例为高考数学的小题,小题不能大做,但是许多学生缺乏数感,只会“死做”——解答题求解法.下面给出数的敏感性的测试: 变式1 已知a>1,b>1,若loga2b+logb2a=4,a2b=b2a,则a=______,b=______. 变式2A={(x,y)|y=x2,x≥0},B={(x,y)|y=2x},A∩B=______. 变式1学生用解答题的方法未必能做下去.变式2在数学水平测试中,许多学生至多写出“{(2,4)}”. 3.2 整体性 任何一个综合性问题,都是一个复杂的符号系统,视复杂结构中某一部分为一个整体,简化结构与运算,也是数学解题的智慧点之一. 图8 3.3 简捷性 图9 例7 如图9,设抛物线y2=2px(其中p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1. 1)求p的值; 2)若直线AF交抛物线于另一点B,过点B与x轴平行的直线和过点F与AB垂直的直线交于点N,AN与x轴交于点M,求M的横坐标的取值范围. (2016年浙江省数学高考文科试题第19题) 图10 此案例中点A的设计(如图10),随后直线AF的设计,为后面的计算带来了极大的方便,这不仅是命题专家的精心设计,也是检验应试者数学智慧的试金石. 在某一个综合问题求解过程中,由题设信息引发的知识点、能力点与智慧点之间是相互依存的,借助于思维导图可以检测或识别或训练思维者,更加清晰地了解问题的本质,把握数学学习的方向. 2017-06-18 陈朝阳(1958-)男,汉族,浙江余杭人,中学高级教师.研究方向:数学教育. O123.1 A 1003-6407(2017)09-09-04
2 培育思维链中的能力点
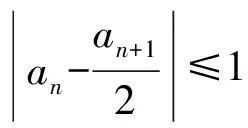
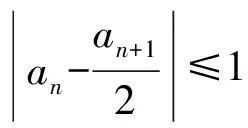
3 积累思维过程的智慧点