都是定义惹的祸——一道易错题的错因分析和教学建议

●孙 鋆 (宁波市第二中学,浙江 宁波 315010)

都是定义惹的祸
——一道易错题的错因分析和教学建议

●孙 鋆
(宁波市第二中学,浙江 宁波 315010)

文章从一道函数题常见的错误出发，寻找错误背后的主因，通过对复合函数定义的合理选取，消除学生在理解上的障碍点，并通过对复合函数定义的纵向梳理，进一步提出切实可行的教学建议.

函数值域;错因分析;复合函数定义

1 问题缘起

三年轮回，笔者转眼又任教于高一数学，而每当讲授到“对数函数”之后，学生在函数问题上的错误频发，其中有这样一个经典问题，常常讲评，但错误率还是极高，现呈现如下.

例1 若函数f(x)=ln(x2+mx+1)的值域为R，求实数m的取值范围.

错误解法 设u=x2+mx+1，由题意知其相应的判别式为Δ=m2-4<0，即m∈(-2,2).

众所周知,这样的结果是错误的.如取m=0，则函数f(x)=ln(x2+1)的值域是[0,+∞),显然与条件矛盾，而这样的解法普遍存在于学生中.为了纠正学生的错误,笔者给出正确的想法:易知y=lgu在u∈(0,+∞)上单调递增且值域为R,欲使原函数值域为R，可设u=x2+mx+1值域为U，则必有(0,+∞)⊆U，因此相应的判别式Δ=m2-4≥0，即m∈(-∞,-2]∪[2,+∞).而令笔者惊奇的是讲评成效甚微，基础中等和偏下的学生还是做错.

2 错因分析

笔者向学生了解他们的解题想法，大多数学生考虑到对数的真数必须大于0，又必须满足集合为R，因此想到Δ<0.不难发现学生将例1和“若函数f(x)=lg(x2+mx+1)的定义域为R，求实数m的取值范围”混为一谈.是学生真的教不会还是学生真的太“笨”而导致屡教不改吗？答案是否定的，其实问题出在教师的教学之中.

2.1 定义“惹祸”

复合函数作为初等数学重要的函数构成方式，尽管现行的高中教材并未给出其定义，但一般教师都会作为补充内容向学生讲授，而上述例1错误解法的原因正好来自于复合函数的定义方式.

文献[1]指出复合函数定义有两大类型8种定义格式，现摘录其中具有代表性的两种定义.1)定义1：设函数y=f(u)的定义域为D1，函数u=g(x)在D上有定义，且g(D)⊆D1，则由下式确定的函数y=f(g(x))称为由函数y=f(u)和函数u=g(x)构成的复合函数；2)定义2：如果y是u的函数y=f(u)，u∈U，而u又是x的函数u=g(x)，x∈X且D={x|g(x)∈U,x∈X}≠φ，则函数y=f(g(x))称为由函数y=f(u)和函数u=g(x)构成的复合函数.

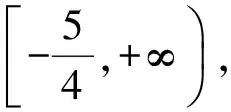
2.2 祸害横流

复合函数作为重要的函数类型常常出现在不同类型的考试中，但实际上很多问题的编制是存在漏洞甚至是错误的.文献[2]主要列举了8种与复合函数相关的错误类型，如：

例2 函数f(2x)的定义域为[-1,1],求f(x)的定义域.

错误解法 令g(x)=2x，由f(2x)的定义域为[-1,1],得

即

此时函数

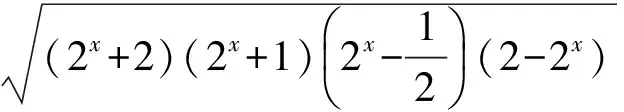
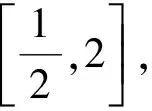
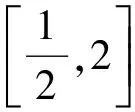
定理1 若函数f(g(x))和g(x)都有已知的显式表达式，且Rg=Df，则f(x)的解析式被唯一确定.

定理2 若函数f(g(x))和g(x)都有已知的显式表达式，且Rg=R，则f(x)的解析式被唯一确定.

事实上2个定理都在强调外函数定义域的确定性.上述由于复合函数中外函数定义域的不确定性导致了诸多错误，这样的错误仍然出现在部分教辅资料之中.

2.3 厘清认知

实际上关于此类问题的争论经历了大约30余年，为了彻底厘清对复合函数定义中相关问题的认识，文献[4]对多年来的相关文献进行了梳理和综述，并且旗帜鲜明地肯定定义2的正确性，在此笔者引入其中几个争论阶段的典型观点.

事实上此种定义符合复合函数定义的科学性.进一步,若记U={u|u=g(x),x∈E}及U*={u|u=g(x),x∈E*}，得到的结论是：若已知复合函数f(g(x))和内函数g(x),而外函数未知，则只可求得E,U,E*,U*，对应外函数的定义域D仅能得到U*⊆D且U*⊆U.若CUU*≠φ，则外函数f(x)必在CUU*上无定义,即D∩CUU*=φ，一般而言较难确定f(x)的定义域D，由此外函数f(x)也不能确定，只能得到在U*上的表达式.文献[4]特别指出，遗憾的是这一正确的结论并未被广大数学教育工作者所熟知,从而导致再次出现“错例—辨析—错例—再辨析”的现象.

由此不难得出例1的正确解法，欲使f(x)=ln(x2+mx+1)的值域为R，只需u=x2+mx+1的值域U⊇(0,+∞)=U*，而学生担心的正是外函数在集合CUU*上无定义而导致无法复合的情况.

3 教学建议

通过查阅文献资料,笔者不禁感叹对于复合函数问题的争论如此热烈，多年来自己对很多问题的认识仍存在错误理解和片面认识.如何尽可能地避免类似的问题再次发生,笔者提出以下建议：

3.1 建议于教材编写者

由于高中阶段复合函数存在的普遍性和重要性，尽管其定义较为抽象，但是几乎所有高中数学教师都会作为补充内容进行教学.为了避免对上述复合函数相关问题进行无谓的争论，建议将此定义编入教材并进行权威发布以正视听.倘若出于课时限制的因素，则可以将此内容作为拓展知识放置到课后的阅读材料.

3.2 建议于教辅编写者翻开各种形形色色的教辅资料，必然会找到相关争论的复合函数定义域或解析式等问题，教辅资料的编写教师应当具有科学的态度和高度的责任感,慎重选择相关复合函数问题的类型，防止将一些错题放入相应的资料中，务必提高资料的质量.

3.3 建议于高中数学教师

教师对一些习以为常的数学问题的解法或结论应保持一种科学的态度、反思的习惯和批判质疑的精神.教师要重视学生中出现的一些易错题，原因或许不仅仅是学生能力的问题，也可能是教师讲授的问题(包括知识或方法等).我国著名的数学教育家张奠宙曾说：数学的核心素养就是“真、善、美”三个维度，即理解理性数学文明的文化价值，体会数学真理的严谨性和精确性；具备用数学思想方法分析和解决实际问题的能力；能够欣赏数学智慧之美.

作为数学教师,要以身示范并积极投身到当下新的课程改革实践中，努力培养学生对数学“真、善、美”的认识和感悟.

[1] 赵光耀.复合函数定义形式的讨论[J].北京工业职业技术学院学报，2004,3(1)：85-88.

[2] 张金良.理清复合函数概念 突破外函数求解疑难[J].中学教研(数学)，2005(8)：43-46.

[3] 陈鸿斌.关于复合函数问题的研究[J].数学学习与研究，2011(3)：117.

[4] 本刊编辑部.争论早就有结论 莫让错例长期留——关于复合函数反编制问题的部分争鸣资料[J].数学教学研究，2014(7)：2-6.

2017-05-26

孙 鋆(1979-)，男，浙江宁波人，中学高级教师.研究方向：数学教育.

O122.1

A

1003-6407(2017)09-07-03