微积分中值定理及其应用

陈 杰

(苏州旅游与财经 高等职业技术学校,江苏 苏州 215104)

【教学改革】

微积分中值定理及其应用

陈 杰

(苏州旅游与财经 高等职业技术学校,江苏 苏州 215104)

文章分析了微积分中值定理及其实践意义,围绕中值定理包含的内在关系,从微分中值定理推广到积分中值定理,总结中值定理在社会应用中的效能估算等方面的具体推广应用,最后给出经济学中应用中值定理的实践案例。

微积分;中值定理;应用

微积分中值定理的出现是一个科学逻辑典型代表,其中聚集了众多数学爱好者和数学家的研究心血,在数学发展史具有举足轻重的突出地位,它是自然科学研究不可缺失的基础。

一、 微分中值定理

微分中值定理可以揭示了函数关系的曲线必然轨迹规律,是数学工具分析数据的基础工具,本文主要以微分中值定理(罗尔(Rolle)定理、拉格朗日(Lagrange)定理、Cauchy定理等)一系列成果及定理之间的关系为研究对象,利用它们来讨论一些社会现象, 包括对供需平衡的求解问题,以及最佳增值效率的求解法等。

(一)罗尔中值定理

若函数满足如下条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)f(a)=f(b),则在[a,b]内至少存在一点ξ∈(a,b),使得:f′(ξ)=0.曲线原理如图1所示。

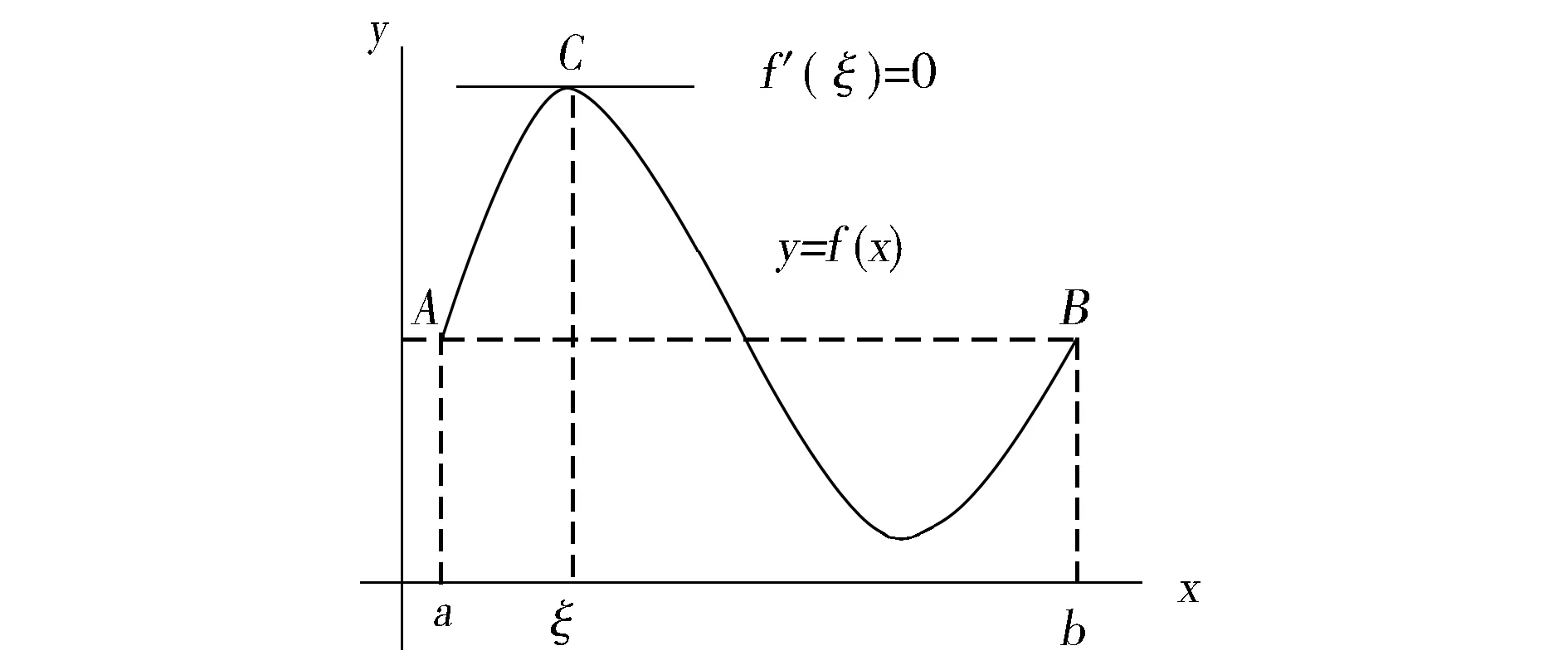
图1 罗尔中值定理曲线

证明:目标函数f(x)在[a,b]上连续,必然有最大值和最小值,最大值和最小值分别用m与M表示。如果有M=m,则函数f(x)在闭区间[a,b]上即为为常数,显然结论成立;如果M>m,结合端点条件f(a)=f(b),容易想到,在(a,b)内至少有一个点ξ,使f(x)取得使得最大值M或最小值m,从而使ξ成为f(x)的极值费马点,由于f(x)在开区间(a,b)内可导,并且f(x)在ξ处可导,故可得结论:f′(ξ)=0.

实践意义:设有一段弧的两端点的函数值相等,如果除两端点之外,各处都有不垂直于水平x轴的切线,那么弧线上至少有一点,使得该点处的切线平行于x轴。罗尔中值定理给我们揭示了许多物极必反现象的必然性存在性。例如:经济分析中的边际分析法是把追加支出和追加收入相比较,计算二者相等时的临界点,即投入资金所得到的利益与成本输出相等时的临界点。构造函数为利润函数,如果追求的目标是取得最大利润,那么当追加收入等于所增加的支出时,这一经济目标就能够实现。

(二)柯西中值定理

假设有函数f(x)及g(x)满足:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)满足g(a)≠g(b)且g′(x)≠0, 则至少存在一点ξ∈(a,b),使得:

柯西定理可以由一般曲线的参数方程证明,可以理解为f(x)与另一函数曲线g(x)在(a,b)上至少存在一点ξ,使得在该点处,f(x)与g(x)曲线的切线是平行的。柯西中值定理产生了微积分学基本定理“牛顿-莱布尼茨公式”, 揭示了定积分或被积原函数或者不定积分函数之间的逻辑关系。

牛顿-莱布尼茨公式的主要内容:如果函数f(x)在区间[a,b]上有定义,并且满足以下条件:(1)在区间[a,b]上可积;(2)在区间[a,b]上存在原函数F(x),则有

牛顿-莱布尼茨公式给我们揭示了社会现象的必然性存在性,找到了解决曲线长度、曲线围成的面积和曲面围成的体积等问题的一般方法。牛顿-莱布尼茨公式简化了定积分的计算过程,条件是只要知道被积函数的原函数,就可以计算出定积分的精确值或者是一定精度下的近似值。

(三)拉格朗日中值定理

拉格朗日(Lagrange)中值定理又称为拉氏定理,是罗尔(Rolle)中值定理的推广,同时也是柯西(Cauchy)中值定理的特殊形式。如果函数f(x))在(a,b)上可导,[a,b]上连续,则必有一点ξ∈(a,b),使得:

拉格朗日(Lagrange)中值定理曲线原理如图2所示。

拉格朗日中值定理的几何意义: 当目标函数在某个闭区间上连续,开区间上可导后,那么在这个函数所表示的函数曲线上,必然一定至少存在一点,使得该点的斜率切线与两个端点连线平行。罗尔中职定理揭示了曲线与水平斜率的存在性,拉格朗日中值定理揭示了函数切线与一般直线斜率相等的存在性关系。

如果目标函数在区间(a,b)上的导数恒为0,那么函数在区间(a,b)上是一个常数。证明:f(b)-f(a)=f′(ξ)·(b-a),ξ∈[a,b],由于已知f′(ξ)=0,f(b)-f(a)=0,即f(b)=f(a).这就是说,在区间内任意两点的函数值都相等。因此函数在区间内是一个常数。

拉格朗日中值定理给我们揭示了社会现象的必然性存在性。对于非匀速直线运动的物体,在其任意运动过程中,至少存在一个位置点(或一个时刻)的瞬时速度等于该过程中的平均速度。 拉格朗日中值定理从根本上证明了:在自由经济交易中,经济利益的获得效益是变动的,不完全都是增值的。从有限理性、交易利润和交易增值的角度考虑,可以进一步推导出商品交易中,合同成交的均衡条件,即:“经济——人”假说里的一般均衡,可以推广到现实社会的广义均衡理性。应用拉格朗日中值定理,可以揭示经济学中的成本边际定价法则,价格函数曲线与边际成本函数曲线相交点(边际成本函数曲线的点斜率大于0、或者边际成本函数曲线的点斜率比价格函数曲线的点斜率更平缓),则这个交点处便是最优定价点。若把需求量与供给量都表示为价格函数,则可以利用积分中值讨论资源剩余等经济问题。

二、 积分中值定理

微积分学说是继欧几里得几何学之后,数学理论应用中最大的一个科学发现,它是联系着经济社会的应用过程发展起来的。17世纪末,人们为了理解和解决社会现象问题(尤其是物理力学问题和经济趋势问题)创立了微积分学说。微积分学说极大地推动了自然科学(物理学、化学、天文学、生物学、经济学和工程技术等)各个分支科学的发展,并在这些学科中越来越广泛的被实践应用。积分中值定理用来表示曲边梯形的面积,可以推导平面曲线之间图形面积、曲面面积和立体体积之间的关系。

积分中值定理:若函数f(x)在闭区间[a,b]上连续,则在积分区间[a,b]上至少存在一个点ξ,使下式成立:

有假设条件: f(x)在闭区间[a,b]上函数连续,设函数f(x)最大值及最小值分别为M和m,即:m≤f(x)≤M.将上式同时在区间[a,b]内积分,可得积分中值定理,即:

因为m≤f(x)≤M是连续函数,由拉格朗日中值定理,必存在一点ξ,使得

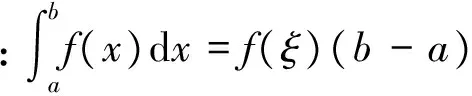
积分中值定理在现代经济管理的应用是广泛的,积分中值定理需要由边际函数的不定积分求解出原经济函数,更重要的是由边际函数的定积分和广义积分法则,求解出原经济函数曲线的点变动特征。由于经济现象较难理解与掌握,积分中值定理在经济分析中的重要地位,积分中值定理成为经济数学的核心内容。例如:在经济利润分析过程中,经常会遇到假设目标函数的导数微分问题,求解这个经济函数的效能问题,这涉及到积分求解的复杂问题。积分运算与导数运算可以视为互逆过程。

三、实践总结

现代社会利用微积分中值定理方法和概念进行分析演绎各种经济学现象,微积分中值定理的作用是作为理论基础,来逻辑分析社会学规律,非单纯的计算工具。例如:经济数学作为研究经济现象的科学,以中值定理为核心内容,研究了经济中各种经济行为和行为者的最优理性选择,探讨了实现有限资源的最优配置方案。微积分中值定理是研究经济最优选择的根本方法,经济与数学具有天然的密切关联性,无论是经济中静态数据的最优化理论,还是经济动态数据的最优化理论中,微积分中值定理是最合适的经济分析工具。人们在经济学中应用数学方法,对经济现象予以定量描述,其研究深度日益增长。

假设以下经济函数,(1)产量函数Q(x);(2)收益函数R(x);(3)需求函数Q(P);(4)成本函数C(x);(5)利润函数L(x)等。边际函数就是上述经济函数的导数,可以由各个经济函数的边际计算,获得其积分函数,最终求出原经济函数,来分析经济现象。在经济管理分析过程中,由各个类型的边际函数求解经济函数的过程,一般都采用不定积分来实现。如果经济需求要求经济函数在某个区间范围内的估算,则可以采用定积分的方式来解决。例如:边际收益、边界需求、边际成本和边际利润等,在产出量x的变动区间[a,b]上的增量,就是边际函数各自源函数在区间[a,b]上的定积分(面积)。

[1]柯希均.微分学在经济分析中的几点应用[J].科技资讯,2010(14):179.

[2]龚友运.微分学在经济分析中的应用浅析[J].科技资讯,2010(15):182-184.

[3]胡乔林.管窥微分学在经济学中的应用[J].中国成人教育,2010(17):188.

[4]郜欣春,贾仙勤.微分学在微观经济学中的几处应用[J].科技经济市场,2011(4):13-14.

[5]龚友运.积分学在经济分析中的应用浅析[J].佳木斯教育学院学报,2011(3):121-122+178.

[6]鲍海峰.高等数学中微积分思想在其它学科的应用[J].山西煤炭管理干部学院学报,2011(3):172-174.

[7]彭友霖.微分学在市场经济中的应用——商品价格与需求关系[J].商场现代化,2007(18):42.

[8]沈奇.微积分及其在经济学中的应用[J].赤峰学院学报(自然科学版),2014(24):6-7.

2017-04-08

陈杰(1980-)，男,江苏丹阳人,苏州旅游与财经高等职业技术学校讲师,硕士,研究方向:数学教育教学。

O13

A

1672-2086(2017)02-0092-03