《解析几何》课程教学内容和教学方式的改革

刘艳梅

(吕梁学院 数学系，山西 离石 033001)

·教材教法研究·

《解析几何》课程教学内容和教学方式的改革

刘艳梅

(吕梁学院 数学系，山西 离石 033001)

依据解析几何课程的特点，结合吕梁学院数学系专业的需求，提出《解析几何》课程改革应从两主面入手.教学内容方面：合理调整解析几何的教学内容；教学内容中应适当融入数学史；教学内容中应安排一定量的实验教学；教学过程中应该融入数学建模思想和案例.教学方式方面：合理采用对比性方式教学；教学中应适度采用多媒体课件.同时，应建立科学合理的学习成绩的评价体系.

解析几何； 教学内容； 数学建模； 数学实验

解析几何这门课程是数学系重要的专业基础课程之一.学习这门课是对中学几何知识的进一步深入与提高，也是学生学习高等几何、微分几何、拓扑学等后期课程的基础.通过该课程的学习，可以培养学生数形结合的几何思维能力；通过将空间的几何结构代数化，数量化，从而为解决力学，物理学和工程技术中的问题提供有力的工具.因此，分析当前解析几何教学中存在的问题，提出一些有效的改革措施对于当前学生素质教育的提高以及创新能力的培养都具有十分重要的意义.

1 解析几何教学内容的改革

1.1 合理调整解析几何的教学内容[1]

数学分析、高等代数和解析几何是三门重要的专业基础课程，我校数学系大一第一学期一直是这三门专业基础课同时平行开设.可事实上，学习解析几何所需的高等代数知识与方法较多，且涉及高等代数的相关内容(主要是行列式、矩阵和线性方程组)滞后，如解析几何第一章的第4，5节向量间共线、共面等线性关系就涉及行列式，线性方程组的知识，但是高等代数课本关于行列式，线性方程组的内容在第二三章才可以学到，这样三门课同时开设，必然影响学生对解析几何这门课程的理解和掌握.

所以教师应根据解析几何的课程体系和学生的实际情况，做出合理的调整.如：先给学生补充行列式，矩阵，线性方程组等相关的知识，再给学生讲解向量与坐标这一章的内容，这样在讲解向量间的线性关系时就水到渠成.或者也可以在第一学期开设数学分析、高等代数这两门课，第二学期再开设解析几何，这样学生已经具备了代数的相关知识，再去理解向量间的线性关系就容易多了.

1.2 将数学史适当融入教学内容中[2]

数学在一些学生的感觉中就是符号和数字的无聊游戏，枯燥而乏味，尤其是数学系的学生，每天上下午的课都是数学，每节课下来都被灌得头晕脑胀的，得不到调节，如果在讲解数学时，适当的插入一点关于数学的历史，会缓解学生的紧张和压力，了解数学的发展历史，激发学生的探索精神.

例如在 “标架与坐标”这一节里，在讲解“笛卡尔坐标系”时，可以讲讲关于笛卡尔本人的故事和事迹，笛卡尔(1596～1650)是法国数学家、物理学家和哲学家，出身于法国的一个小镇，父亲是一名律师，笛卡尔从小就失去母亲，身体又比较孱弱，所以8岁时才开始进入学校，由于父亲很宠爱他，专门跟学校协商允许他每天可以不去早起晨练而在床上多休息一会，据说因为这个原因竟然让他养成了躺在床上思考问题的习惯.笛卡尔的学习不拘泥课本，喜欢博览群书，所以他的思路和想法比较开阔.据说笛卡尔直角坐标系“就是他在床上晨思时看见天花板上的一只苍蝇在爬行，突发灵感而创立的.

笛卡尔的这种勤于思考，勇于探索的精神会给学生的学习产生一定的激励作用.

1.3 教学内容中应安排一定量的实验教学[3]

解析几何中的几何图形，有很多是空间立体图形，要在平面上手工绘画出立体感很强，直观逼真的图形是很难的.如果能让学生利用一些数学软件，自己编写简单的程序，绘制出解析几何课本中的立体图形，如椭圆，抛物面等，会激发学生的兴趣和求知欲，锻炼学生的实际操作能力，提高教学效果.因此，在教学内容中还应该安排一定量的实验教学，要让学生掌握一些常用的数学软件如：Matlab、flash等，提高学生的实际动手能力.但选取的实验内容要适合学生对软件掌握的水平，一般是软件实现越简单越好，逐步提高，不可急于求成.

1.4 将数学建模思想融入教学内容中

虽然解析几何的中心内容中不涉及数学建模，但是将数学建模中的实际问题带入教学过程中，可以强化学生对数学知识的应用，激发学生的求知欲和创新性，培养学生应用知识的能力.在解析几何的教学中，举一些生活中的实例，如电影放映机的聚光灯泡的反射面利用的就是椭圆面，建筑工程上的冷却塔就是利用单叶旋转双曲面的直纹性构建而成的；酒瓶、酒杯、花瓶等是利用旋转曲面原理烧制而成的；卫星的天线、雷达天线、太阳灶、探照灯、聚光灯、望远镜等都是利用抛物线的原理制成的.又如 2008 年北京奥运会的主体育场“鸟巢”整个建筑造型呈马鞍形.通过这些生活中的实例让学生体会到立体图形在日常生活中的应用，感受到数学是有生命力的，而不是抽象的，遥不可及的.在讲解平面直线的相关问题时，可以举一些简单的生产规划问题，如“建筑方面的设计、面积、采光、曲面的抗压性研究”等模型，指导学生通过建立平面直角坐标系，并结合代数知识画出可行域，从而求出最优解.

2 解析几何教学方式的改革

2.1 合理采用对比性教学[4]

解析几何的教学内容中，有好多内容研究方法类似，如向量的数量积、向量积和混合积、平面方程和直线方程、二次曲面，将这些研究方法类似的内容放在一起讲解，会收到事半功倍的效果.

例如：

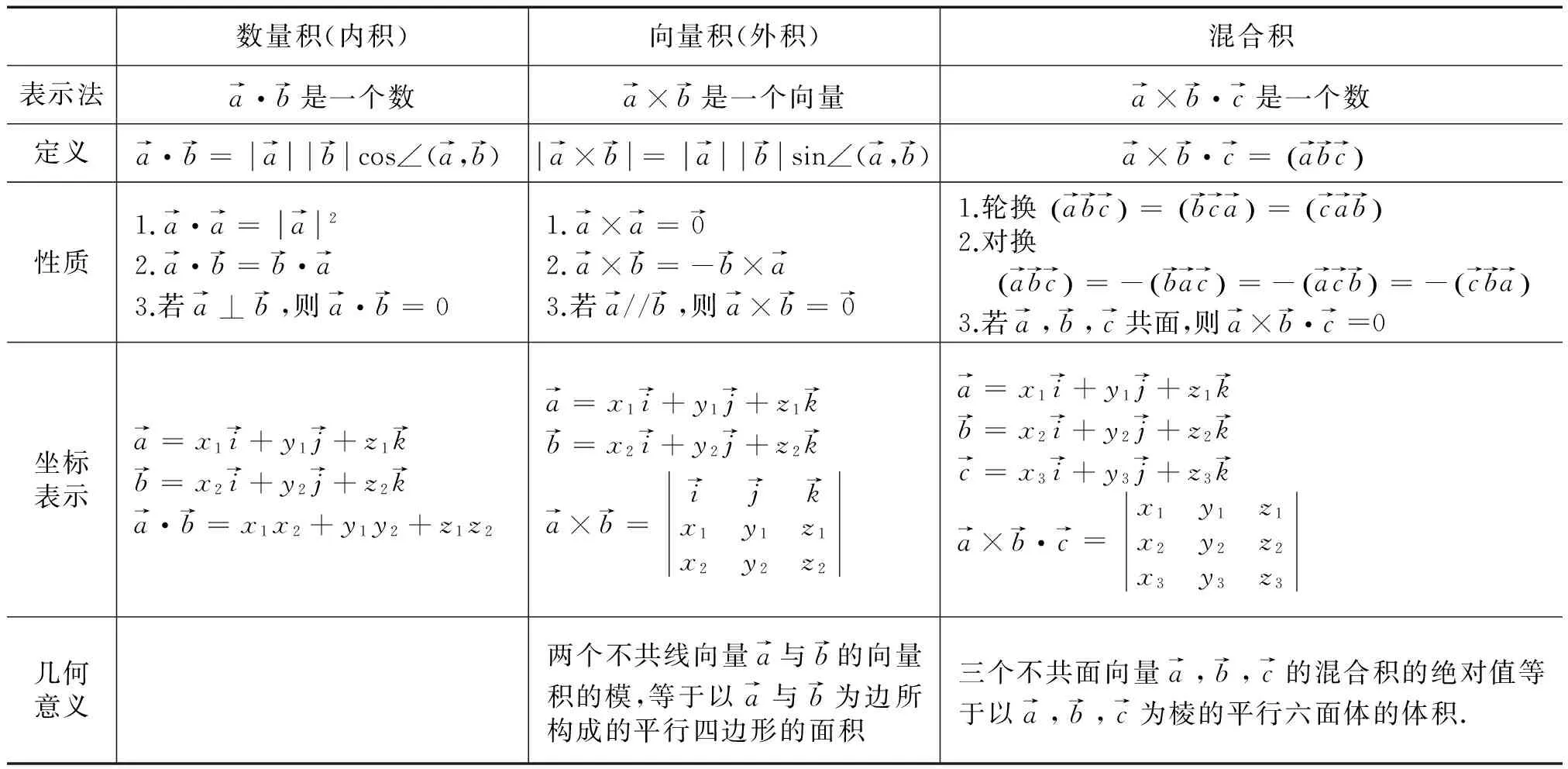
数量积(内积)向量积(外积)混合积表示法a→·b→是一个数a→×b→是一个向量a→×b→·c→是一个数定义a→·b→=a→b→cos∠(a→,b→)a→×b→=a→b→sin∠(a→,b→)a→×b→·c→=a→b→c→()性质1.a→·a→=a→22.a→·b→=b→·a→3.若a→⊥b→,则a→·b→=01.a→×a→=0→2.a→×b→=-b→×a→3.若a→//b→,则a→×b→=0→1.轮换a→b→c→()=b→c→a→()=c→a→b→()2.对换 a→b→c→()=-b→a→c→()=-a→c→b→()=-c→b→a→()3.若a→,b→,c→共面,则a→×b→·c→=0坐标表示a→=x1i→+y1j→+z1k→b→=x2i→+y2j→+z2k→a→·b→=x1x2+y1y2+z1z2a→=x1i→+y1j→+z1k→b→=x2i→+y2j→+z2k→a→×b→=i→j→k→x1y1z1x2y2z2a→=x1i→+y1j→+z1k→b→=x2i→+y2j→+z2k→c→=x3i→+y3j→+z3k→a→×b→·c→=x1y1z1x2y2z2x3y3z3几何意义两个不共线向量a→与b→的向量积的模,等于以a→与b→为边所构成的平行四边形的面积三个不共面向量a→,b→,c→的混合积的绝对值等于以a→,b→,c→为棱的平行六面体的体积.

这样对比起来学习，学生会理解的更深刻，教学效果会更好.

2.2 采用多媒体课件辅助性教学[5]

一方面，由于近年来课时的不断缩减，教师既要完成教学内容，还要有好的教学效果，的确很难，采用多媒体辅助教学，可节省好多作图和擦黑板的时间，教师有更多的时间给学生讲解，与学生互动交流.

另一方面，解析几何这门课程具有它本身的特殊性，好多几何图形靠教师的手工绘画是达不到直观的效果的.通过多媒体中图形准确直观的展示，再结合老师的讲解，能够培养学生丰富的空间想象力，加深学生对几何图形的理解.

例如，在讲解柱面和旋转曲面形成过程时，利用多媒体课件动态展示曲面的形成过程.学生在观看的同时，既激发了听课的兴趣，也加深了对图形的理解.同时还有美的享受.

再比如认识二次曲面的形状，利用“平行截割法”，即曲面与一组平行平面相交，通过平行平面的截口来研究曲面的图形.教师采用PPT的动画演示不同平面截二次曲面所得平面曲线的变化过程，从而揭示了的曲面形成的本质.

结合多媒体课件将空间图形展示给学生，使课堂教学具有直观性，趣味性，同时也有利于发挥学生的空间想象力，加深学生对知识的理解，这的确是一种有效的教学方法.但是，也不是解析几何所有的教学内容都适合使用PPT，比如很多公式的推导，定理的证明还需要教师以传统的方式引导学生，培养学生严谨的逻辑推理能力.因此，多媒体课件的教学只是辅助性的，是帮助教师优质高效地完成教学.

3 解析几何考核方式的改革

传统的闭卷考试只注重解析几何理论的考核，而缺乏学生应用知识能力的评价，这样的考核方式不能全面反映学生理解知识，应用知识的综合能力，所以需建立更科学合理的成绩评价体系，比如，可将解析几何的考核分为平时作业、章节小结、实验、小论文、期末考试五个模块. 每个模块占有一定的比重(平时作业占10%、章节小结10%、实验10%、小论文10%、期末考试60%)，最后取其总评成绩.这样的考核方式，除了要求学生掌握课本的理论知识外，还注重学生实际操作能力和应用知识能力的训练，从各个环节上上调动学生的学习积极性，有利于学生综合能力的培养.

4 结语

通过对解析几何的教学内容和教学方式的改革，以期达到培养学生理解知识和应用知识的能力，同时在今后的工作中还需在教学理念、教育方法和手段上不断创新，使我们的教学质量能够与时俱进，达到满足社会对人才的需要.

[1]吕林根,许子道.解析几何:第四版[M].北京:高等教育出版社,2005.

[2]朱家生.数学史[M].北京:高等教育出版社,2004.

[3]赵亚男,牛言涛.MATLAB在解析几何教学中的应用[J].长春大学学报,2011，21(4).

[4]季全宝.普通本科院校“解析几何”教学探讨[J].长春理工大学学报,2012(7).

[5]邵光华,王培合.高等院校数学专业解析几何课程改革研究[J].大学数学,2011(27).

2017-01-19

吕梁学院教学改革项目(JYYB201507).

刘艳梅(1978-)，女，山西柳林人，讲师，研究方向为微分方程.

G642.0

A

2095-185X(2017)02-0078-03