一种特殊补图的最小特征值

吴 翰，李 雨，孙 威，王振东，黄 星

(1.安庆师范大学 物理与电气工程学院,安徽 安庆 246133;2.安庆师范大学 计算机与信息学院,安徽 安庆 246133;3.安庆师范大学 数学与计算科学学院,安徽 安庆 246133)

·数学研究·

一种特殊补图的最小特征值

吴 翰1，李 雨2，孙 威3，王振东1，黄 星1

(1.安庆师范大学 物理与电气工程学院,安徽 安庆 246133;2.安庆师范大学 计算机与信息学院,安徽 安庆 246133;3.安庆师范大学 数学与计算科学学院,安徽 安庆 246133)

邻接矩阵是表示顶点之间相邻关系的矩阵, 通常它的最小特征值就是图的最小特征值. 本文针对一种特殊补图的最小特征值, 刻画了该类图最小特征值达到极小的唯一图.

邻接矩阵；补图；最小特征值

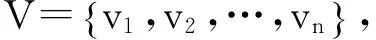
关于图的谱半径有不少的研究成果.然而，相对于谱半径，最小特征值的研究较少.自范益政等人[10]在论文中刻画了树的补图的最小特征值后，该研究引起了一些图论学者的关注[11-15]，得到了一些成果，且所研究的图的补图均为连通图.本文仍然从补图的角度出发研究了给定阶数的特殊补图的最小特征值，并刻画了此类图最小特征值达极小的唯一图.

下面我们引进一些定义.设G=(V,E)为n阶简单图，对于向量X∈Rn，如果存在一个从V到X中值的映射φ，使得对于任意u∈V有Xu=φ(u)，则称X定义在G上.

我们发现对于任意向量X∈Rn，有

(1)

若λ是A(G)对应于特征向量X的特征值，则由特征值的定义，当且仅当X≠0，对于每个v∈V，有

(2)

我们称等式(2)为G关于X的特征等式.另外，对于任意单位向量X∈Rn，有

λmin(G)≤XTA(G)X,

(3)

当且仅当X是G的第一特征向量时等式成立.

Gc表示图G的补图.显然有A(Gc)=J-I-A(G)，其中J,I分别表示n阶全1矩阵和单位矩阵.因此，对于任意向量X∈Rn，有

XTA(G)X=XT(J-I)X-XTA(G)X.

(4)

记G(p,q)是阶为p+q+2(p≥0,q≥1)的特殊图，它是由两个不相交的完全图Kp,Kq以及两个孤立点v4,v5通过以Kp的一个顶点v1与Kq的一个顶点v2为端点的边v1v2和Kq的另一个顶点v3与两个孤立点v4,v5为端点的边v3v4，v3v5连接的图.如图1所示.特别地，当q=1时,v2=v3；当p=0时，G(p,q)=G(0,q)为Kq的一个顶点v3与两个孤立点v4,v5为端点的边v3v4,v3v5连接的图.

图1 G(p,q)

引理1[16]设A是一个实对称n×n阶矩阵,B为A的m×m阶主子阵,且λ1(A)≥λ2(A)≥…≥λn(A),λ1(B)≥λ2(B)≥…≥λm(B)分别为A与B的特征值,则对于i=1,2,…,m，有λn-m+i(A)≤λi(B)≤λi(A).

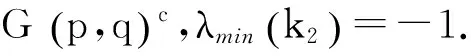
(5)

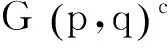
情形1：当p=0时.由等式(2)与(5)知Kq中除v3点外所有的点在X中对应的值相同，记为X1，v4,v5点在X中对应的值相同，记为X3.记Xv3=X2，记λmin(G(0,n-2)c)=λ，这样由等式(2)可以得到

将上式转换成矩阵等式(B-λI)X′=0,其中X′=(X1,X2,X3)T,

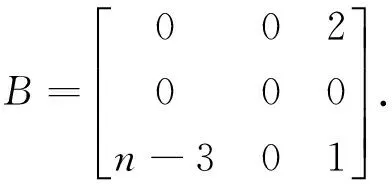
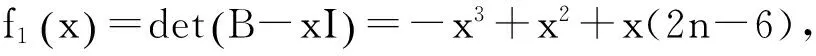
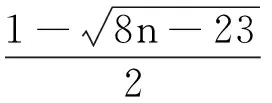
情形2：当p=1时.由等式(2)与(5)知Kq中除v2,v3两点外所有的点在X中对应的值相同，记为X1，v4,v5点在X中对应的值相同，记为X5.记Xv1=X2,Xv2=X3,Xv3=X4，记λmin(G(1,n-3)c)=λ，再由等式(2)可以得到

将上式转换成矩阵等式(B-λI)X′=0,其中X′=(X1,X2,X3,X4,X5)T,

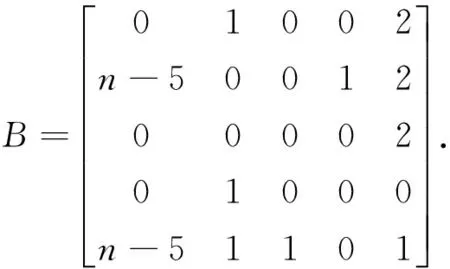
令f2(x)=x4(1-x)+x3(3n-10)+x2(3n-16)-x(4n-18).

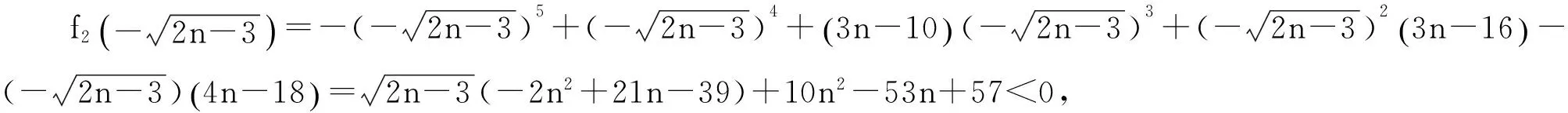
情形3：当q=1时.由等式(2)与(5)知，Kp中除v1点外所有的点在X中对应的值相同，记为X1，v4,v5点在X中对应的值相同，记为X4.记Xv1=X2,Xv2(v3)=X3,记λmin(G(n-3,1)c)=λ，这样由等式(2)可以得到

将上式转化成矩阵等式(B-λI)X′=0，其中X′=(X1,X2,X3,X4)T,

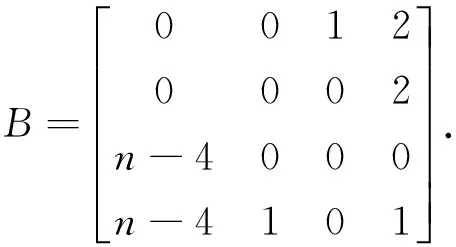
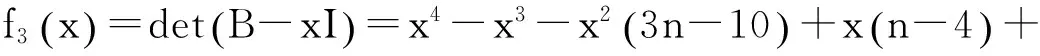
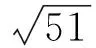
情形4：当p,q≥2时.由等式(2)与(5)可知Kp中除v1点外所有的点在X中对应的值相同,记为X1,在Kq中除v2,v3两点外所有的点在X中对应的值相同，记为X4，v4,v5点在X中对应的值相同，记为X6.记Xv1=X2,Xv2=X3,Xv3=X5,，记λmin(G(p,q)c)=λ，这样由等式(2.2)可以知

将上式转换成矩阵等式(B-λ1I)X′=0，其中X′=(X1,X2,X3,X4,X5,X6)T，

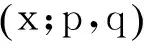
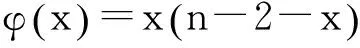
(1)若p≥q+2,当x<-8时，我们有

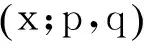
>x2(x2(p-q-1)+x(3p-3q+1)-(3p-3q-1))

>x2(37(p-q)-71)>0.

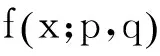
(2)若q≥p+1,当x<-8时，且q≥p+3时，我们有

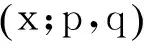
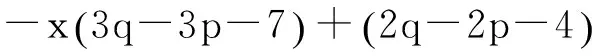
>x2(x2(q-p-1)+x(3q-3p-7)-(3q-3p-5))

>x2(37(p-q)-3)>0.

当x<-8时，且q=p+1时，我们有

当x<-8时，且q=p+2时，我们有

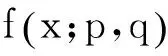
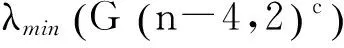
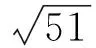
再综合情形1、2、3、4知结论成立.

[3]Y.Z.Fan，Y.Wang，Y.B.Gao.Minimizing the least eigenvalues of unicyclic graphs with application to spectral spread[J].Linear Algebra Appl，2008(429).

[4]R.Liu，M.Zhai，J.Shu.The least eigenvalues of unicyclic graph with n vertices and k pendant vertices[J].Linear Algebra Appl，2009(431).

[6]Y.Y.Tan，Y.Z.Fan.The vertex(edge) independence number，vertex(edge) cover number and the least eigenvalue of a graph[J].Linear Algebra Appl，2010(433).

[7]Y.Wang，Y.Z.Fan.The least eigenvalue of a graph with cut vertices [J].Linear Algebra Appl，2010(433).

[8]M.L.Ye，Y.Z.Fan，D.Liang.The least eigenvalue of graphs with given connectivity[J].Linear Algebra Appl，2009(430).

[9] G.D.Yu，Y.Z.Fan，Yi Wang.Quadratic forms on graphs with application to minimizing the least eigenvalue of signless Laplacian over bicyclic graphs[J].Electronic Journal of Linear Algebra，2014(27).

[10]Y.Z.Fan，F.F Zhang，Y.Wang.The least eigenvalue of the complements of tree [J].Linear Algebra Appl，2011(435).

[11]S.C.Li and S.J.Wang.The least eigenvalue of the signless Laplacian of the complements of trees[J].Linear Algebra Appl，2011(436).

[12]Y.Wang ，Y.Z.Fan，X.X.Li，et al.The least eigenvalue of graphs whosecomplements are unicyclic[J].Discussiones Mathematicae Graph Theory，2013,35(2).

[13]G.D .Yu，Y.Z.Fan.The least eigenvalue of graphs [J].Math.Res.Expo，2012(6).

[14]G.D.Yu ，Y.Z.Fan.The least eigenvalue of graphs whose complements are 2-vertex or 2-edge connected[J].Operations Research Transactions，2013(2).

[15]W.haemers.Interlacing eigenvalues and graphs[J].Linear Algebra Appl，1995(227-228).

2017-02-03

国家自然科学基金资助项目(11604002，51607004).

吴 翰(1993-)，男，安徽枞阳人，在读硕士,研究方向为图形图像处理.

O157.5

A

2095-185X(2017)02-0009-04