一种自底向上的最大频繁项集挖掘方法

赵 阳，吴廖丹

(江南计算技术研究所，江苏 无锡 214083)

一种自底向上的最大频繁项集挖掘方法

赵 阳，吴廖丹

(江南计算技术研究所，江苏 无锡 214083)

频繁项集挖掘是关联规则挖掘中最关键的步骤。最大频繁项集是一种常用的频繁项集简化表示方法。自顶向下的最大频繁项集挖掘方法在最大频繁项集维度远小于频繁项数时往往会产生过多的候选频繁项集。已有的自底向上的最大频繁项集挖掘方法或者需多次遍历数据库，或者需递归生成条件频繁模式树，而预测剪枝策略有进一步提升的空间。为此，提出了基于最小非频繁项集的最大频繁项集挖掘算法(BNFIA)，采用基于DFP-tree的存储结构，通过自底向上的方式挖掘出最小非频繁项集，利用最小非频繁项集的性质进行预测剪枝，以缩小搜索空间，再通过边界频繁项集快速挖掘出最大频繁项集。验证实验结果表明，提出算法的性能较同类算法有较为明显的提升。

最大频繁项集；关联规则挖掘；FP-tree；最小非频繁项集；边界频繁项集

0 引 言

关联规则挖掘的概念由Agrawal等于1993年提出[1-3]，用于发现大量数据中项目或项目集之间有趣的关联或相关关系，同时提出了经典的关联规则挖掘算法—Apriori。此后众多学者对Apriori算法进行了改进。但Apriori系列算法需要多次扫描数据集的固有缺陷，使其在处理大型数据集时面临无法容忍的时间开销。针对这一问题，Han等[4]提出用FP-tree对数据进行压缩存储以及基于FP-tree的频繁模式挖掘方法—FP-growth。该算法只需扫描数据集两次，避免了Apriori算法需多次扫描数据集的缺陷。

在关联规则挖掘过程中，频繁项集的挖掘是算法主要的开销，而最大频繁项集涵盖了所有的频繁项集，因此最大频繁项集挖掘的优化对于提升关联规则挖掘算法的整体效率至关重要。已有的最大频繁项集挖掘算法包括：Max-Miner[5]、Pincer-Search[6]、FP-Max[7]、DMFI[8]、DMFIA[9]等。Max-Miner突破了传统的自底向上的挖掘方法，尽早地进行了剪枝，而Pincer-Search则采用双向搜索策略，这两种算法在最大频繁项集挖掘过程中都产生了过多的候选项集，并且需多次扫描数据集；FP-Max采用FP-tree的数据压缩表示，避免了多次扫描数据集，但需递归地生成条件FP-tree，影响了算法的效率；DMFI将自底向上和自顶向下的搜索策略进行有效合并,在海量数据库中发现最大频繁项集和仅需要发现最大频繁项目集的数据挖掘应用中效果显著,但该算法仍需多次重复扫描数据库,计算项目集的支持数；DMFIA采用FP-tree的数据结构及自顶向下的搜索策略，避免了递归的生成条件FP-tree，但当最大频繁项集的维度相比频繁项的数目较小时，将产生大量的候选频繁项集，而在大量数据集的实际应用中，最大频繁项集的维度往往远小于频繁项的数目[10]。文献[11]提出的基于降维的最大频繁项集挖掘算法(BDRFI)，采用数字频繁模式树对FP-tree进行了一定的优化，并从提高FP-tree的生成速度、减少超集检测的次数等方面进行了改进，性能相比DFMIA有了较大提高，但仍然存在自顶向下算法的固有缺陷。文献[12]通过获取低维的非频繁项集的信息对较高维度的最大候选频繁项集进行快速降维，但是应该对于哪些搜索层次计算非频繁项集，以及对于每一层计算哪些非频繁项集，仍需进一步研究确定。而显然计算并记录所有的非频繁项集是不可行的，浪费了存储空间，而且增加了超集检测的开销。

以上问题表明，针对最大频繁项集维度较小的数据集，提升算法性能的关键在于：避免自顶向下的搜索所产生的大量候选项集；选择尽可能少的非频繁项集进行预测剪枝。对此，提出了一种基于最小非频繁项集的最大频繁项集挖掘算法(BNFIA)。该算法通过自底向上的方法挖掘最小非频繁项集，在该过程中用子集检验的方法进行预测剪枝，同时记录中间结果的边界频繁项集，并应用边界频繁项集快速生成最大频繁项集。

1 相关知识

设I={i1,i2,…,im}是m个不同项目的集合。给定事务数据库D,对于项目集X⊆I,X在D中的支持数是指D中包含X的事务数,记为X.countD；X在D中的支持度是指D中包含X事务的百分比,记为X.supD。

关于频繁项集、非频繁项集、最大频繁项集的定义参见文献[13]。

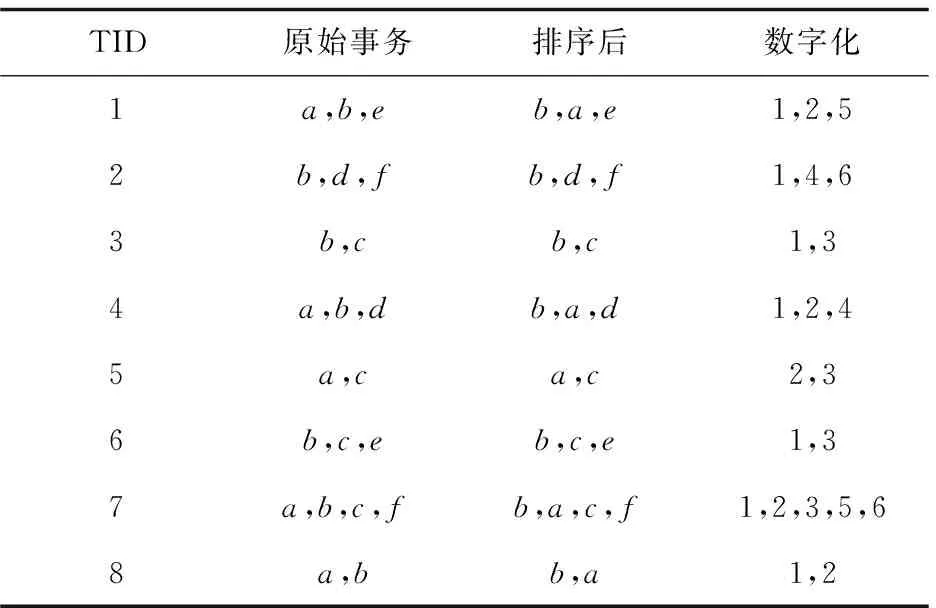
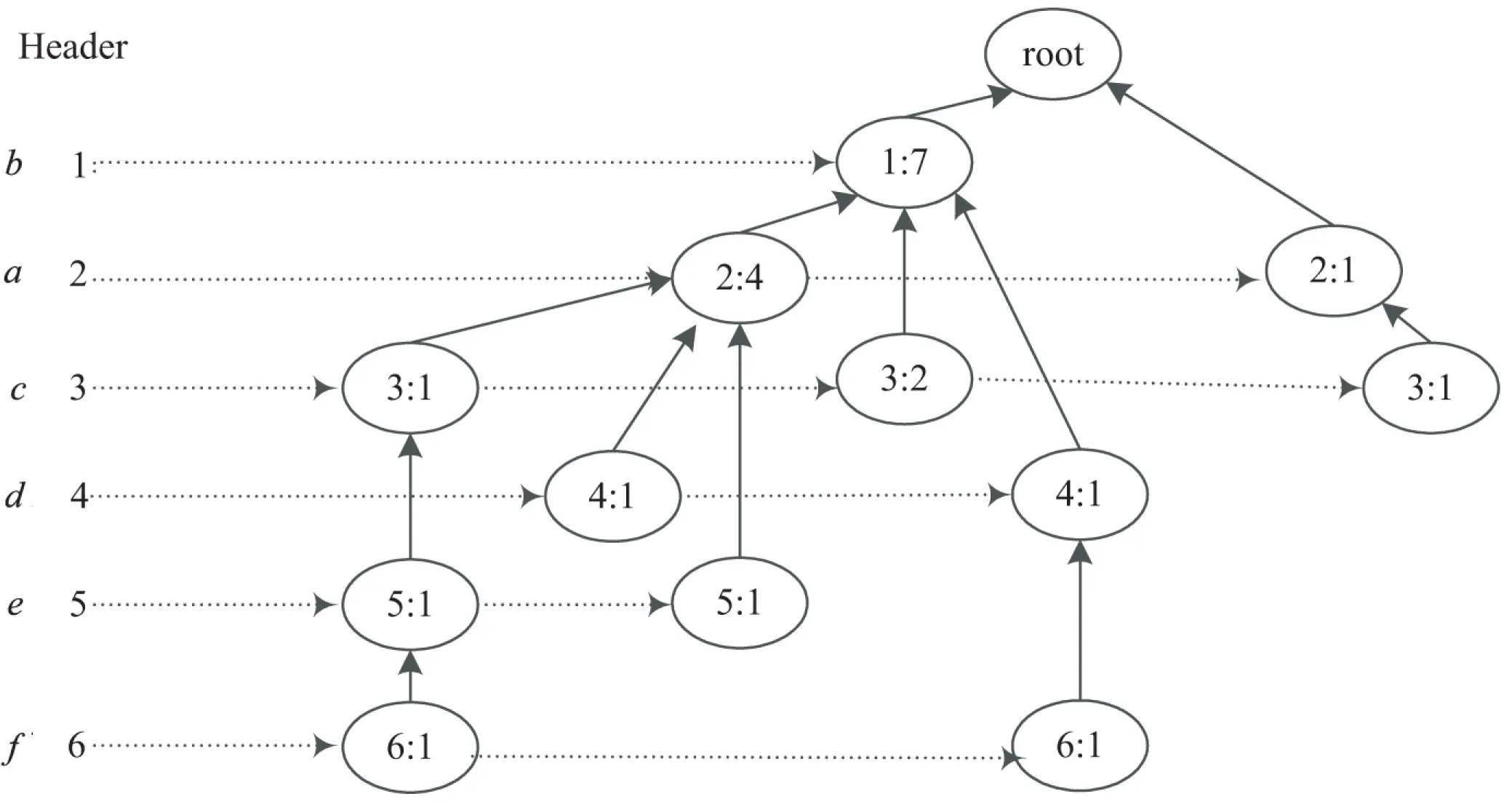
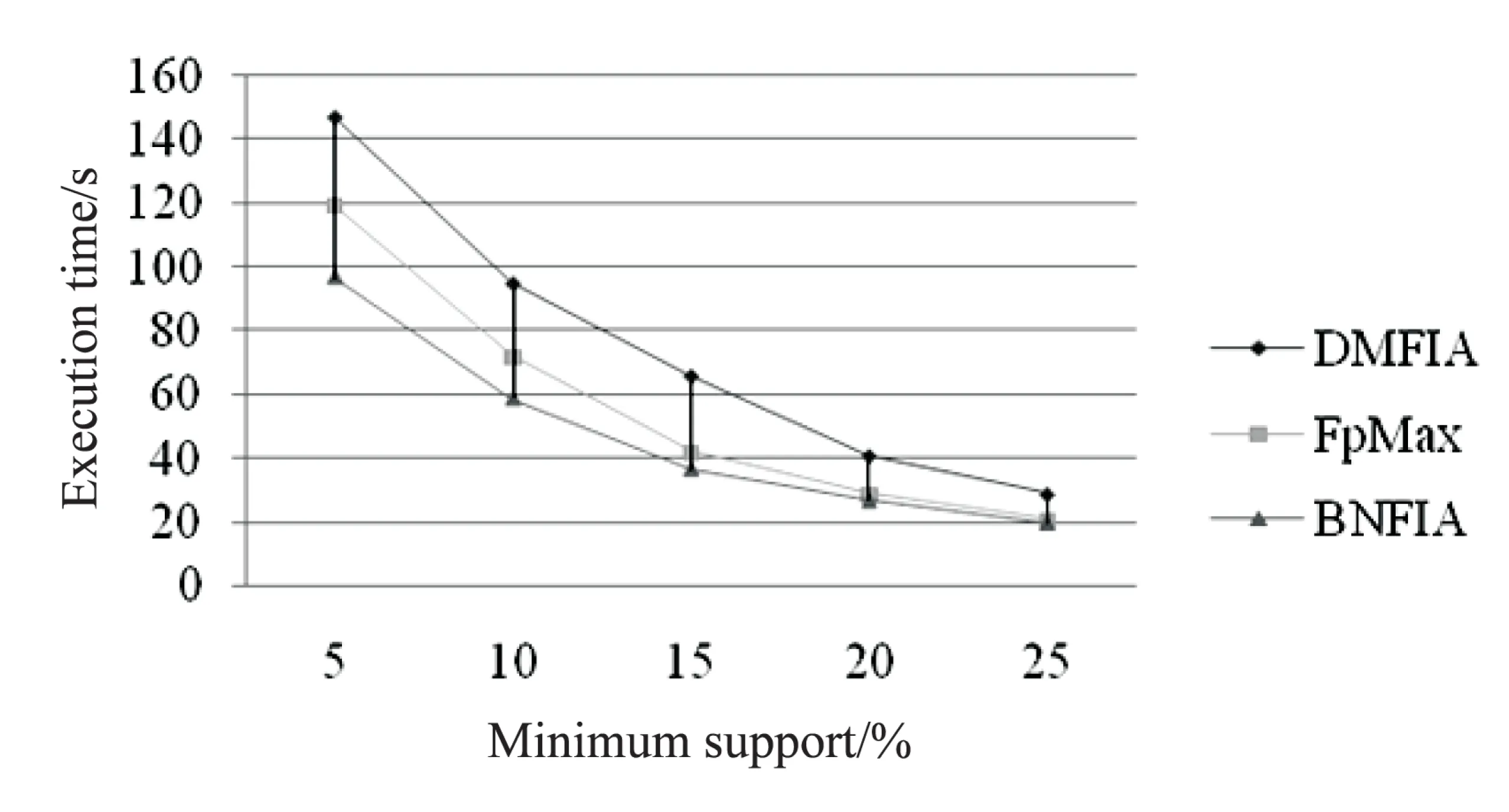
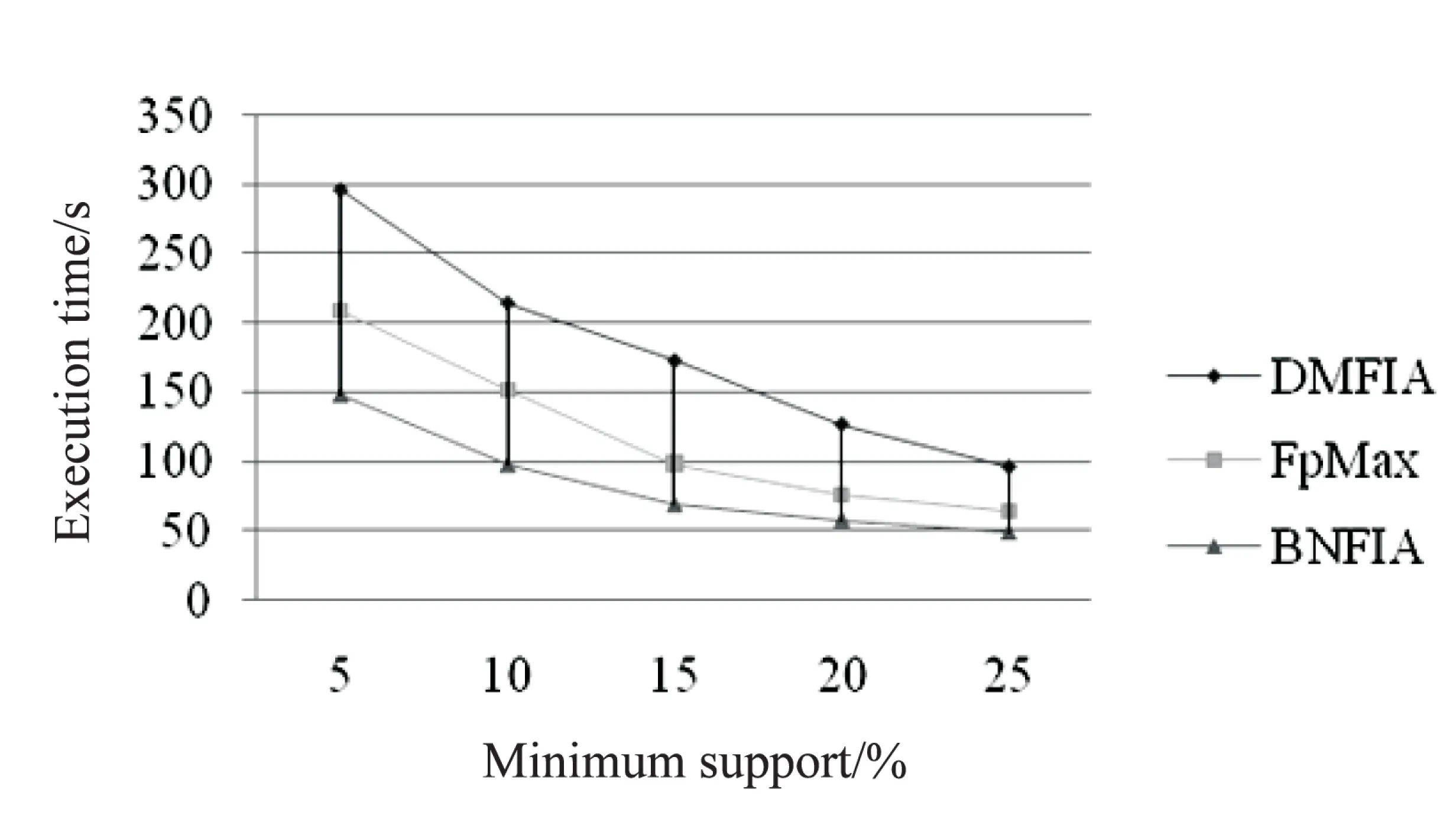
定义1：对于项目集X⊆I,如果X.supD

定义2：对于k-项集X，其所有(k-1)-项子集称为X的直接子集，其所有(k+1)-项超集称为X的直接超集。

性质1：任何一个非频繁项集至少存在一个最小非频繁项集的子集。

证明：对于任何一个非频繁k-项集Xk：

(1)若其所有直接子集Xk-1都是频繁项集，则Xk为最小非频繁项集；

(2)令k=k-1，对于所有非频繁项集Xk-1，重复步骤(1)。

由于1-项集是频繁的，因此一定会找到一个所有直接子集为频繁项集的最小非频繁项集为X的子集，证毕。

定义3：对于项目集X⊆I，如果X.supD≥s，并且存在Y是X的直接超集且Y.supD

性质2：最大频繁项集一定是边界频繁项集。

证明：由最大频繁项集的定义可知，其所有超集都是非频繁的，因此最大频繁项集一定是边界频繁项集。

性质3：若X为频繁项集，则X的直接超集有可能是最小非频繁项目集。

性质4：如果X是最大频繁项集，则X的任何真子集都不是最大频繁项集。

定理1：设降序频繁项头表为{1,2,…,k}，若存在t-项频繁项集X={1,2,…,t}，则以t为后缀生成的不包含X的所有项集必定是非最大频繁项集[11,14]。

2 DFP-tree与DMFIA

频繁模式树(FP-tree)是一种树的结构，它的每个节点对应一个项，事务数据库中的某条事务在该树中的表现为从根到某个子孙节点的路径集合。由于某些路径会有重叠，所以FP-tree可以通过共享这些重叠的项来压缩保存数据。在FP-tree中，每个节点由4个域组成[4]:节点名称(node-name)、节点计数(node-count)、节点链(node-link)(用于指向树中具有相同node-name的下一个节点)及父节点指针(node-parent)。同时为方便树的遍历，FP-tree还包含一个频繁项头表Htable，它由两个域组成:项目名称(item-name)、指向FP-tree中具有相同item-name的首节点的指针(head of node-link)。

数字频繁模式树(Digital Frequent Patten tree，DFP-tree)是对传统FP-tree的一种改进，其核心思想是“字符串或汉字串的匹配速度要比数字集合慢”，以此来达到提高超级检验速度的目的。其改进的主要方法是用频繁项按照支持度降序排列的序号来代替频繁项本身，关于DFP-tree的构建方法和详细介绍参见文献[11]。

DMFIA采用FP-tree的存储结构和自顶向下的搜索策略。它采用双重循环的方式挖掘最大频繁项集，外层循环是在MFCS非空状态下进行，内层循环是由自底向上的方式进行处理，若MFCS中项集的支持度大于等于最小支持度阈值，则将该项集加入最大频繁项集(Maximum Frequent Sets，MFS)。对非频繁项集，通过循环每次删除该项集中的一个项来产生新的候选项集，对于新的候选项集，需要判断在MFS和MFCS中是否存在超集，若不存在则将其加入MFCS中，否则删除。该算法的主要问题是，当最大频繁项集的维度相对于频繁项的数目较小时，会产生大量的最大频繁候选项集。

3 基于最小非频繁项集的最大频繁项集挖掘算法

3.1 算法思想

如前文所述，当最大频繁项集的维度相对于频繁项的数目较小时，采用自顶向下的搜索策略往往会产生大量的候选项集。而已有的自底向上的搜索策略有些需要递归产生FP-tree，有些没有充分利用非频繁项集进行剪枝，或者用于剪枝的非频繁项集过于冗余。而BNFIA采用DFP-tree的数据压缩存储方式，参考DMFIA自顶向下挖掘最大频繁项集以及运用超集检测进行剪枝的思想，提出自底向上挖掘最小非频繁项集并运用子集检测进行剪枝，同时保存中间结果中的边界频繁项集，最后所有的边界频繁项集都包含在中间结果的边界频繁项集与最小非频繁项集的直接超集之中。

性质1说明算法使用最简化的非频繁项集进行了充分的剪枝，性质2保证了算法的正确性，同时采用了性质3包含的剪枝策略。

3.2 算法流程

算法1：最小非频繁项集挖掘算法。

输入：D的数字频繁模式树DFP-tree，频繁项目头表Header({1,2,…,k})，最小支持度阈值s；

输出：D的最小非频繁项目集(MUFS)，边界频繁项集(BFS)。

(1)MUFS=∅,BUFS=∅,BFS={{1,2,…,endItem}}

//{1,2,…,endItem}可能是边界频繁项集，将其加入BFS以确保完备性

(2)MFCS={最后一个项目大于endItem的2项集}

//因为已经确定1项集为频繁项集，故初始化为2项集

(3)While(MFCS!=∅) do begin

(4)for(i=k;i>endItem;i--) do begin//定理1

(5)MFCSi={c|c∈MFCS andc的最后一项为i};

(6)MFCS=MFCS-MFCSi;

(7)调用过程ComputeCount(DFP-tree,Header,MFCSi);

//计算项目集在D中的支持数

(8)for allm∈MFCSido begin

(9)ifm.supD

(10)MUFS=MUFS∪{m}

(11)else

(12)ifm.iteritor(1)==1 then

(13)BFS=BFS∪{m}//同前，确保结果的完备性

(14)for(j=m的最后一个项+1;j≤k;j++) do begin//性质3

(15)if {j}+m不是MUFS中某元素的超集 then

(16)MFCS=MFCS∪{{j}+m}

(17)else

(18)BFS=BFS∪{m}

(19)end

(20)end

(21)end

(22)end

算法2:最大频繁项集的计算。

输入：D的最小非频繁项目集，边界频繁项集；

输出：D的最大频繁项集(MFS)。

(1)MFS=∅,CFS=∅

(2)for(allm为MUFS中元素的直接子集) do begin

(3)CFS=CFS∪{m}

(4)end

(5)CFS=CFS∪BFS

(6)对CFS中集合元素按照集合大小降序排列

(7)for(allm∈CFS) do begin

(8)ifm不是MFS中某元素的子集 then

(9)MFS=MFS∪m

(10)end

算法ComputeCount参见文献[9]。

3.3 算法实例

表1所示为一组事务的原始形式、按照频繁项降序排列以及数字化后的结果。图1所示为该事务集对应的DFP-tree。endItem=2,MFCS={{1,3},{2,3},{1,4}{2,4}{3,4},{1,5},{2,5},{3,5},{4,5},{1,6},{2,6},{3,6},{4,6},{5,6}};第1轮循环后，MFCS=∅,MUFS={{1,2,3},{2,4},{3,4},{3,5},{4,5},{2,6},{3,6},{4,6},{5,6}}，BFS={{1,2},{1,3},{1,4},{1,5},{1,6},{1,2,5}}。

经过算法2得到MFS={{1,3},{1,4},{1,6},{1,2,5}}。

表1 事务数据集实例

图1 事务数据集实例的数字频繁模式树

4 实验结果及分析

实验中在8 G RAM，Intel Core i5-2430M CPU 2.40 GHz，Windows7操作系统上用Java实现了DMFIA、FPMax、BNFIA算法。图2采用的测试数据集为mushroom，包含8 124条记录，记录平均长度为23，共有115个蘑菇属性。

图2 mushroom数据集上算法的执行时间对比

为了更好地验证算法在频繁项数目较大，最大频繁项维度较小的数据集下的挖掘效率，实验中随机生成了具有200个属性、事务平均长度为15的10 000条事务组成的事务集，在该事务集上采用上述三种算法进行了最大频繁项集挖掘的对比实验，结果如图3所示。

从以上两种数据集的挖掘中可以看出，当频繁项数目较多而最大频繁项集维度较小时，BNFIA的运行时间明显少于DMFIA和FpMax，并且在支持度较高的情况下执行效率的差别仍然明显。这是因为随着最小支持度的提高，最大频繁项集的维度降低，BNFIA算法采用自底向上的搜索策略以及基于最小非频繁项集的剪枝策略，相比自顶向下搜索的DMFIA，产生了更少的频繁项集，而与FpMax相比则不需要递归地生成条件频繁模式树。

图3 随机生成的数据集上算法的执行时间对比

5 结束语

针对最大频繁项集维度远小于频繁项数量的数据的特点，提出了最大频繁项集挖掘算法—BNFIA。该算法采用DFP-tree的数据存储结构，避免多次扫描数据库；采用自底向上的搜索策略，利用最小非频繁项集作为非频繁项集信息的最简化表示，用于搜索剪枝，避免了自顶向下的搜索策略在最大频繁项集维度较小而频繁项较多时会产生过多的候选项集的缺陷；同时通过边界频繁项集迅速确定最大频繁项集，而不必记录所有的频繁项集，减少了候选项集的数量；与FpMax算法相比该算法无需递归地生成条件频繁模式树，因此减少了产生的时间开销。

[1] Imielinski T，Swami A, Agrawal R．Mining association rules between sets of items in large database[C]//Proceedings of 1993 ACM SIGMOD conference on management of data.New York:ACM，1993:207-216．

[2] Han J, Kamber M. Data mining:concepts and techniques[M].Beijing:High Education Press,2001.

[3] Fan M, Meng X F.Data mining:concepts and techniques[M].Beijing:Mechanical Industrial Press,2001.

[4] Han J，Pei J，Yin Y.Mining frequent patterns without candidate generation[C]//Proceedings of the 2000 ACM-SIGMOD international conference on management of data．New York:ACM,2000:1-12．

[5] Bayardo R. Efficiently mining long patterns from databases[C]//Proceedings of the ACM SIGMOD international conference on management of data.New York:ACM,1998:85-93.

[6] Lin D，Kedem Z．Pincer-search:a new algorithm for discovering the maximum frequent set[C]//Proceedings of the 6th European conference on extending database technology．Ber-lin:Springer-Verlag，1998:105-119．

[7] Grahne G，Zhu J．High performance mining of maximal frequent itemset[EB/OL]．[2014-07-06]．http://www．docin．com/p-773109811．html．

[8] 路松峰，卢正鼎.快速开采最大频繁项目集[J].软件学报，2001，12(2)：293-297.

[9] 宋余庆，朱玉全，孙志挥，等．基于FP-tree的最大频繁项目集挖掘及更新算法[J]．软件学报，2003，14(9):1586-1592．

[10] 吉根林，杨 明，宋余庆，等．最大频繁项目集的快速更新[J]．计算机学报，2005，28(1):128-135．

[11] 钱雪忠，惠 亮．关联规则中基于降维的最大频繁模式挖掘算法[J]．计算机应用，2011，31(5):1339-1344．

[12] 杨鹏坤，彭 慧，周晓锋，等．改进的基于频繁模式树的最大频繁项集挖掘算法—FP-MFIA[J].计算机应用，2015，35(3):775-778.

[13] Tan Pangning.数据挖掘导论:英文[M].北京：人民邮电出版社,2006.

[14] 秦亮曦，史忠植．SFP-Max—基于排序FP-树的最大频繁模式挖掘算法[J]．计算机研究与发展，2005，42(2):217-223．

A Bottom-up Method for Mining Maximum Frequent Itemsets

ZHAO Yang，WU Liao-dan

(Jiangnan Institute of Computer Technology,Wuxi 214083,China)

Mining frequent itemsets is the most critical step in mining association rules.Maximum frequent itemsets is a common compressed representation of frequent itemsets.In mining maximum frequent itemsets,the top-down methods would produce lots of candidate itemsets when the dimensions of maximum frequent itemsets is smaller than the number of frequent itemsets.The existing bottom-up methods need either traversal in database many times or building FP-tree recursively,and the prediction pruning strategies have further room for improvement.The algorithm of discovering maximum frequent itemsets based on minimum non-frequent itemsets named BNFIA has been proposed,which uses storage structure based on FP-tree and digs out the minimum non-frequent itemsets through a bottom-up approach first,then prunes with the minimum non-frequent itemsets to narrow search space for acquiring the maximum frequent itemsets fast through boundary frequent itemsets.Experimental results show that the proposed algorithm has performed better than the algorithm with same type.

maximum frequent itemsets;association rules mining;FP-tree;minimum non-frequent itemsets;boundary frequent itemsets

2016-09-09

2016-12-14 网络出版时间：2017-06-05

国家科技重点专项“核高基”(2015ZX01040-201)

赵 阳(1991-)，男，硕士研究生,研究方向为数据挖掘、文本分析及可视化。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170605.1511.082.html

TP311

A

1673-629X(2017)08-0057-04

10.3969/j.issn.1673-629X.2017.08.012