一种透视投影下的非刚体迭代重构方法
戴龙利,曹蓉蓉,阮宗才,2
(1.东南大学 学习科学研究中心,江苏 南京 210000;2.东南大学 儿童发展与学习科学教育部重点实验室,江苏 南京 210000)
一种透视投影下的非刚体迭代重构方法
戴龙利1,曹蓉蓉1,阮宗才1,2
(1.东南大学 学习科学研究中心,江苏 南京 210000;2.东南大学 儿童发展与学习科学教育部重点实验室,江苏 南京 210000)
透视投影下的非刚体三维重构中既存在着非刚体形变也存在着透视形变,同时区分两种形变是比较困难的。大多数非刚体三维重构算法通常进行了简化,只考虑正交投影下的非刚体重构。为了解决透视投影下的非刚体重构问题,将基于形状基的EM算法和仿射迭代方法进行有机结合,提出了一种适用于透视投影的新算法。该算法利用EM算法可解决数据点丢失问题的优势以及仿射迭代方法结果较为精确的优点,可提高计算的鲁棒性和重构效果。为验证算法的有效性,选择5 000帧面部表情连续变化的Frank图像序列进行了迭代重构仿真实验。实验结果表明,所提出算法在透视投影模型下具有较好的鲁棒性以及重构效果,能准确地实现动态场景下对人脸的非刚体三维结构重构。
透视投影;非刚体;形状基;三维运动重构
0 引 言
三维运动重构(Structure from motion)是计算机视觉领域的基本问题,即从二维的图像序列中获取刚体或非刚体三维结构和运动信息。尽管刚体三维运动重构的方法已经得到了广泛的研究和应用,但是真实世界中的很多场景和对象都是动态和非刚体的。目前来说,刚体情况已经基本解决,而非刚体问题逐渐成为研究热点,并取得了显著成果。
Bregler等[1]将刚体的矩阵分解方法进行了扩展,将刚体形状基引入到形变约束的场景结构中。但是这种方法只有在场景下的所有图像序列的特征点都能被追踪到才能奏效,对于数据丢失的情况则没有办法重构。Torresani等[2]引入EM算法,用于解决数据缺失的情况。Gonzalez-Mora等[3]提出了一种从大量数据的不同表情和姿势的图片中学习三维人脸模型的三维重构方法。Lladó等[4]提出了一种新颖的从未标定的立体相机对中获取可变形对象欧氏三维结构的方法。Khan[5]针对缺少约束的非刚体三维运动重构问题,提出了一种新的基于约束的框架来约束解空间。国内专家学者近期在这方面也得出了一些成果[6-13]。
在透视投影下的非刚体三维重构中,既存在非刚体形变也存在透视形变,同时区分两种形变是比较困难的。大多数非刚体三维重构算法,为了方便处理,只考虑正交投影下的非刚体重构。Torresani等提出的基于形状基的EM算法[2],有效解决了在非刚体重构过程中的数据丢失问题,但仍然采用的是正交投影。Christy等[14]提出一种透视投影下的仿射迭代方法,可以将模型拓展到透视投影下,逐步消除透视变形带来的影响。
在此基础上,将基于形状基的EM算法和仿射迭代方法有机结合,提出了一种在透视投影下的迭代非刚体重构算法。该算法利用EM算法可解决数据点丢失问题的优势以及仿射迭代方法结果较为精确的优点,可提高计算的鲁棒性和重构效果。并通过仿真迭代实验对算法的有效性进行了验证。
1 相关工作
1.1 基于形状基的EM算法
根据文献[2],给定一系列的图像追踪点,利用EM算法,能够在部分追踪点缺失的情况下恢复出非刚体的运动和变形。在整个重构过程中定义如下相关变量:J表示总点数,T表示总帧数,t表示当前帧数。
正交投影方程为:
Pt=Rt(St+Dt)+N
(1)
其中,Pt为图像追踪点;Rt为旋转矩阵;Dt为平移矩阵;N(0,σ)为零均值高斯噪声;St为形状矩阵,表示为:
(2)

E步骤:考虑已知的运动和形状估计ψ,在t帧时,对隐变量Zt的分布做出估计。定义q(Zt)为t时刻的概率密度分布:
q(Zt)=p(Zt|Pt,ψ)
(3)

M步骤:最小化期望负对数。
Q(P1,P2,…,PT|ψ)=Eq(Z1),q(Z2),…,q(ZT)[-logp
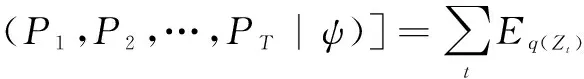
(4)


补充缺失跟踪点:如果有部分的追踪点丢失了,那么在M步骤里同样没有这些数据。用(*)表示对应的缺失的数据行,用P*表示一帧数据中数据不能被追踪到的元素,它们能够这样被估计:
(5)
1.2 透视投影下的仿射迭代方法
根据文献[3],假设摄像机是标定的,可以忽略内参数。在透视投影下,空间点Stj在图像平面的投影为stj,有如下关系:
mtjstj=RtStj+Dt
(6)

根据式(6),可以求得:
(7)
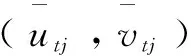
(8)
由式(8)可知,透视投影和正交投影之间的差别在于投影因子λtj,定义一个追踪矩阵:
(9)
因此,能够用正交投影法恢复方程(9)中的标量λtj,得到物体透视投影下的修正投影点。
2 透视投影下的迭代非刚体重构方法
如果图像序列存在遮挡的话,就会存在采不到数据的特征点,追踪矩阵就会还有缺失的数据项,采用EM算法正是为了解决这个问题,同时也能增强算法的鲁棒性。其次,透视投影过程中存在透视变形,使用文献[3]提供的迭代方法,将投影结果逐步迭代到透视投影下。针对这些问题,提出在透视投影下的迭代非刚体重构方法,能够较好地在真实透视投影模型下对非刚体进行三维重构。
迭代算法如下:
(2)更新跟踪矩阵W;
(3)根据基于形状基的EM算法,得到形状Stj,Dt;
(4)由λtj=1+εtj=1+rj3Stj/dtz估算新的λjt;
(5)如果λjt不收敛,回到第(2)步。
经过数次迭代,最终逼近透视投影模型下的结果。
3 实验结果与分析
实验选择了5 000帧面部表情连续变化的Frank图像序列来验证算法的有效性。Frank图像序列每帧图像具有68个特征点。实验中,选取了简化的摄像机模型,假设所有的特征点都在图像中心,并且摄像机的参数在投影过程中不会改变。图1给出了第101、149和191帧图像的原始图像及其对应的正视、侧视和俯视重构结果。
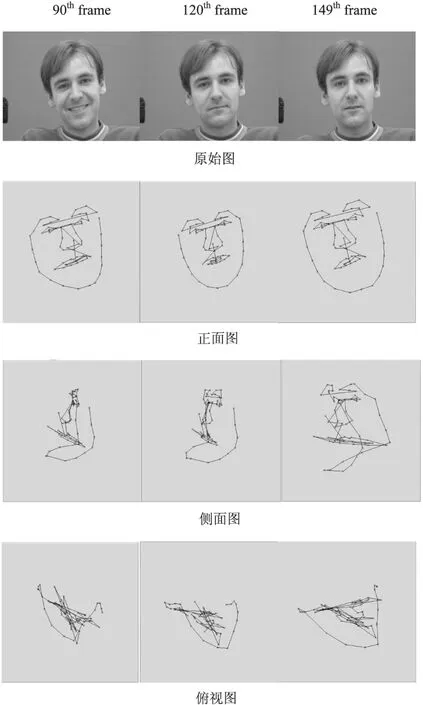
图1 基于形状基非刚体运动重构结果
从图中可以看出,该方法能够准确地重构动态场景下人脸的非刚体三维结构。
为了定量分析在透视投影模型下重构非刚体结构方法的性能,表1给出了基于EM算法的形状基方法和所采用迭代法重构结果的重投影误差的对比结果,重投影误差定义如下:
(10)
其中,W为原始测量矩阵;WF为重构三维结构的重投影矩阵。

表1 改进矩阵分解法和迭代方法的重投影误差
从表1看出,相比基于EM算法的形状基方法,提出的迭代法能够很好地改进形状基方法的准确性。
图2中,第一步迭代的误差对应于正交投影方法所产生的投影误差。从图中可以看出迭代算法的改进之处。所采用的迭代算法在第五到第六步之后开始收敛。
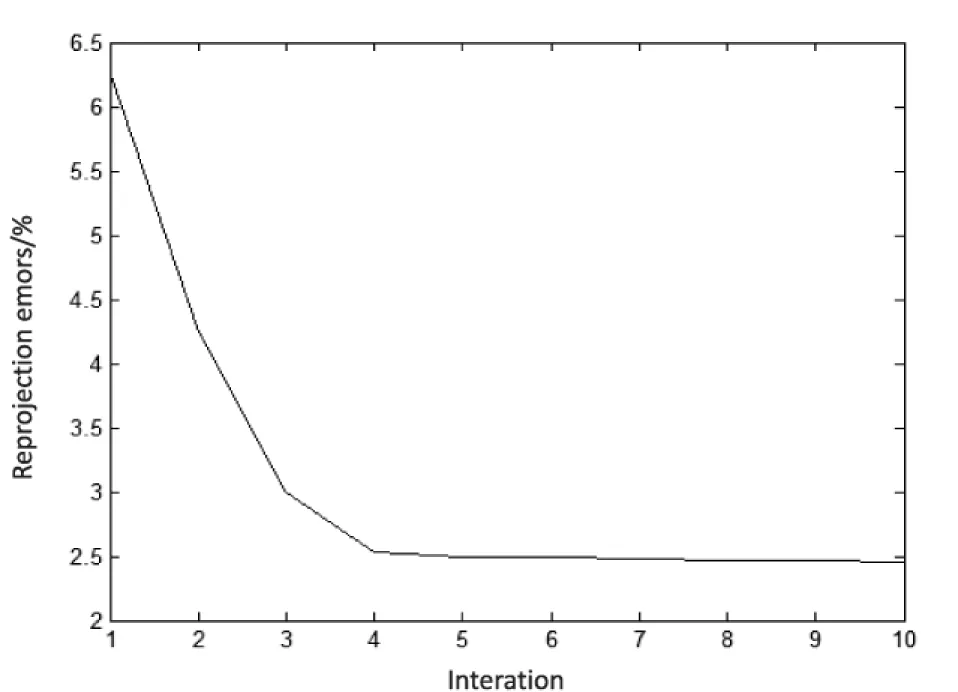
图2 提出的迭代法每次重投影误差
因为引入EM算法能够有效解决数据丢失的问题,因此,图3给出了在丢失特征点情况下所用迭代法的重投影误差。可以看到迭代算法在数据丢失时依然有较好的鲁棒性。

图3 数据丢失的重投影误差
4 结束语
透视投影下的非刚体三维重构中同时区分非刚体形变和透视形变是比较困难的。大多数非刚体三维重构算法通常进行了简化,只考虑正交投影下的非刚体重构。为了解决透视投影下的非刚体重构问题,在基于形状基的非刚体三维运动重构研究以及从动态图像序列中恢复非刚体三维结构和运动信息的基础上,将基于形状基的EM算法和仿射迭代方法有机结合,并假设非刚体的三维形状是刚性形状基的加权线性组合,在正交投影下运用EM算法,解决追踪点丢失的问题,提高算法的鲁棒性。同时使用仿射迭代的方法,逐步修正投影点到透视投影模型下,逼近全透视投影摄像机模型下的结果,较好地实现了透视投影模型下较好的鲁棒性以及重构效果。
[1] Bregler C, Hertzmann A, Biermann H.Recovering non-rigid 3D shape from image streams[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2000:690-696.
[2] Torresani L,Hertzmann A,Bregler C.Learning non-rigid 3D shape from 2D motion[C]//NIPS.[s.l.]:[s.n.],2004:1555-1562.
[3] Gonzalez-Mora J,Torre F D L,Guil N,et al.Learning a generic 3D face model from 2D image databases using incremental structure-from-motion[J].Image and Vision Computing,2010,28(7):1117-1129.
[4] Lladó X,Bue A D,Oliver A,et al.Reconstruction of non-rigid 3D shapes from stereo-motion[J].Pattern Recognition Letters,2011,32(7):1020-1028.
[5] Khan I.Non-rigid structure-from-motion with uniqueness constraint and low rank matrix fitting factorization[J].IEEE Transactions on Multimedia,2014,16(5):1350-1357.
[6] 林义闽,吕乃光,娄小平,等.用于弱纹理场景三维重建的机器人视觉系统[J].光学精密工程,2015,23(2):540-549.
[7] 彭亚丽,刘侍刚,裘国永.一种线性迭代非刚体射影重建方法[J].西安交通大学学报,2015,49(1):102-106.
[8] 吴 悦,翁小兰.非刚体三维运动图像重建优化模型仿真[J].微电子学与计算机,2015,32(5):157-160.
[9] 李水平,吴 雨.一种融合纹理的三维图像重建快速实现方法[J].计算机技术与发展,2014,24(5):138-141.
[10] 闫晓萌.基于稀疏逼近的非刚体三维运动重建研究[D].杭州:浙江理工大学,2016.
[11] 张珊珊,吕东辉,孙九爱.近光源光度立体三维重建误差分析[J].计算机技术与发展,2015,25(1):168-172.
[12] 彭亚丽,刘侍刚,贲晛烨,等.基于非刚体的线性迭代相机自标定方法[J].电子学报,2016,44(5):1051-1054.
[13] 刘彦宏,王洪斌,杜 威,等.基于图像的树类物体的三维重建[J].计算机学报,2002,25(9):930-935.
[14] Christy S,Horaud R.Euclidean shape and motion from multiple perspective views by affine iterations[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(11):1098-1104.
An Iterative Non-rigid Reconstruction Method under Perspective Projection
DAI Long-li1,CAO Rong-rong1,RUAN Zong-cai1,2
(1.Research Center for Learning Science,Southeast University,Nanjing 210000,China;2.Key Laboratory of Child Development and Learning Science of Ministry of Education,Southeast University,Nanjing 210000,China)
Non-rigid three-dimensional reconstruction under perspective projection has both non-rigid deformation and perspective deformation,and it is difficult to distinguish them.Most of the non-rigid three-dimensional reconstruction algorithm is usually simplified,only considering the non-rigid body reconstruction in orthogonal projection.In order to solve the problem of non-rigid body reconstruction in perspective projection,after combination of the EM algorithm based on shape basis and the affine iterative method,a new algorithm for perspective projection is proposed.It uses the advantage of EM algorithm that can solve the problem of data point loss and of affine iterative method that is more accurate and thus can improve the robustness and reconstruction effect.In order to its effectiveness,an iterative reconstruction simulation experiment has been performed by selecting 5 000 consecutive Frank images with facial expressions,which indicates that it has good robustness and reconstruction effect under the perspective projection model,and can accurately reconstruct the non-rigid three-dimensional structure of human face under dynamic scene.
perspective projection;non-rigid;shape basis;three dimensional reconstruction
2016-09-29
2016-12-29 网络出版时间:2017-07-05
全国教育科学规划教育部重点课题(GQA106013);江苏省高校基本科研业务费基础科研扶持项目(2242016K40040)
戴龙利(1991-),男,硕士,研究方向为神经信息工程;阮宗才,博士,讲师,研究方向为计算机视觉、可视化技术、神经信息工程。
http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1652.070.html
TP301
A
1673-629X(2017)08-0016-04
10.3969/j.issn.1673-629X.2017.08.004

