基于Spark的K-means安全区间更新优化算法

李玉波，杨余旺，唐 浩，陈光炜

(1.南京理工大学 计算机科学与工程学院，江苏 南京 210094；2.普渡大学，印第安纳州 西拉法叶 47906)

基于Spark的K-means安全区间更新优化算法

李玉波1，杨余旺1，唐 浩1，陈光炜2

(1.南京理工大学 计算机科学与工程学院，江苏 南京 210094；2.普渡大学，印第安纳州 西拉法叶 47906)

每次K-means算法更新聚类中心后，会对数据集中所有的点迭代计算它们与最新聚类中心的距离，进而获取点的最新聚类。这种全局迭代计算的特征导致传统K-means算法时间效率低。随着数据集增大，算法的时间效率和聚类性能下降过快，因此传统的K-means算法不适合大数据环境下的聚类使用。针对大数据场景下的时间效率和性能优化问题，提出了一种基于Spark的K-means安全区间更新优化算法。在每次更新聚类中心后，该算法更新安全区间标签，根据标签是否大于0每次判断落在该区间内的全部数据的簇别，避免计算所有点与中心的距离，减少因全局迭代造成的时间和计算资源开销。算法基于Spark机器MLlib组件的点向量模型优化了模型性能。通过衡量平均误差准则和算法时间两个指标，进行了优化K-means与传统K-means聚类的性能对比实验。结果表明，所提出的优化算法在上述两个指标上均优于传统的K-means聚类算法，适用于大数据环境下的数据聚类场景。

K-means；安全区间；Spark；大数据；时间效率

0 引 言

聚类分析是数据挖掘领域中的重要分析，广泛应用于网络入侵检测、医学图像处理、文本检索、生物信息学等领域[1]。K-means算法是针对具有连续特征属性的数值型数据进行聚类划分，因为其较好的伸缩性和简单的实现方式而被广泛采用[2]。传统K-means聚类算法通过不断迭代与重新计算聚类中心直至收敛进行聚类，具有两个明显的制约因素。由于初始聚类中心的随机性，当算法在完备数据空间进行不完全搜索时，使得局部极值点成为了目标函数的最大值，无法得到全局最优解[3-4]。因此，传统的K-means算法对初始聚类中心敏感，且每次迭代需要进行全局元素的遍历。当陷入局部最优解时会造成算法收敛时间过长、计算量增大的问题。随着数据量的增加，在大数据环境下，传统聚类算法的收敛时间过长，计算量增加明显，造成算法时间复杂度较高，执行时间变长，性能下降明显。

为解决大数据条件下的算法执行时间过长问题，海沫等[5]在并行计算基础上提出将数据集分散到不同计算引擎的分布式聚类方案，其基本思想是：先在各子节点进行局部聚类，然后主节点对各子节点的局部聚类结果进行全局聚类，进而得到全局聚类模型，最后主节点将全局聚类模型返回各子节点，各子节点根据该模型进行聚类更新。各子节点传递给主节点的仅是该节点数据集的部分代表点，存在忽略关键点的可能。会造成分布式聚类算法的聚类准确性低于集中式聚类算法。要提高聚类结果准确性，必须为主节点传递更多数据。导致增加站点间的通信量造成节点计算量倾斜。因此，分布式聚类算法同样面临平衡聚类准确性和时间复杂度的问题。

为解决K-means并行计算中数据偏移的问题，赵卫中等[6]提出使用Hadoop平台的并行计算引擎进行处理，将聚类中心每次存入HDFS中作为全局变量。虽然能缓解局部极值问题，但是增加了大量的磁盘IO操作，造成算法时间效率过低[7-8]。

为此，提出了一种基于Spark的K-means安全区间更新优化算法。将数据集的点映射到安全区间，每次聚类中心更新后，避免全局迭代计算所有点与聚类中心的距离。仅通过判断安全区间标签来确定该区间内所有点的簇别，减少了因进行数据集全局迭代计算产生的时间耗费和性能开销。算法利用Spark栈MLlib组件的点向量计算模型，优化大数据环境下向量点距离的并行计算模型和过程，进一步优化算法执行时间，减小平均误差，以提高聚类精度。

1 K-means安全区间更新优化算法

传统的K-means算法更新聚类中心后，需要迭代计算数据集内所有的点与k个聚类中心之间的距离，并判断距离点最近的聚类中心，重新划分点到新簇。这种全局迭代方法由于计算量较大，时间复杂度增长明显，大数据环境下聚类性能下降很快[2,9]。

K-means的安全区间更新优化算法将点按照其跳转到其他簇的最近距离，将数据集的点划分为k个安全区间。每次聚类中心更新后，通过更新安全区间标签，确定该区间内所有点是否需要变更簇别。标签小于等于0的安全区间中点被检出并重新映射对应的安全区间，直到所有点均落在标签为正数的安全区间，即获得点对应的簇别。

1.1 安全距离算法

基于Spark的K-means安全区间更新优化算法核心是将数据集中的点按照安全距离映射到各自距离标签范围内的安全区间。其中，安全距离是指聚类中心更新后，数据集中的某点仍然能够保持在原聚类簇中的最小偏差值，即从原簇跳转到距离该点最近的另一个簇需要变更的最小距离。安全区间是指能够容纳这些安全距离的连续区间，其标签为区间的终点值。

如图1所示，以3-簇为例，该数据集的聚类中心分别为C0,C1,C2，且P是原属于C0簇的某点，P到各聚类中心的距离分别记为dPC0，dPC1，dPC2。点P要从原C0簇跳转到C1或C2，至少移动的距离为：

Δp=min(dPC1-dPC0,dPC2-dPC0)

(1)

其中，Δp为点P留在C0簇的安全距离。即，当聚类中心移动Δf后，只要偏移后仍满足Δp-Δf>0，则点P簇别不会发生变化。同理，将数据集中所有满足该关系的点映射到一个安全距离区间，标记为Δp。当经过K-means算法迭代，聚类中心发生变更后，只需检验对应的安全区间标签是否满足Δp-Δf>0，可按组将安全区间内的点是否发生簇别变更全部检出。

图1 安全距离示意图

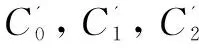
(2)

(3)

联立式(2)和式(3)：

(4)

要使安全区间标签更新后区间内的点仍留在原簇，区间内点的安全距离要满足式(4)。

1.2 安全区间更新优化算法

按数据集中点的安全距离可以将所有的点映射到不同的安全区间。K-means更新聚类中心后，用新聚类中心相对原聚类中心的最大偏移量更新安全区间的标签，以实现同时对整个区间内的所有点簇别的更新，减少迭代后的距离计算次数。算法流程如下：

算法1：K-means安全区间更新优化算法。

(1)定义一个常量WIDTH作为区间长度。

(2)定义一系列区间Ii=[i*WIDTH,(i+1)*WIDTH]，并将它们的标签记为i*WIDTH。其中i为连续的正整数。

(3)选择k个聚类中心。

(4)对于数据集中的每个点，计算安全跳转距离Δp=min(dPCl-dPCs)。其中，Cs为距离该点最近的中心，Cl为其他的簇中心，s=1,2,…,K且s≠l。

按i*WIDTH<Δp<(i+1)*WIDTH将所有的点映射到步骤(2)中的区间i*WIDTH中。

(6)使用聚类中心移动的距离D更新区间Ii的标签。对所有的区间标签减去2*D，即将区间内的值向边界靠近2*D距离。

(7)检出那些区间标签小于或等于0的点，并返回步骤(4)，直到所有的点都被检出。

与传统聚类算法不同的是，优化算法将所有的点按安全距离映射到安全区间，每次更新聚类中心后，只更新对应的区间标签即可检出区间全部点的簇别，减少了簇内点距离计算和比较造成的时间开销，提高了算法的时间效率。

设数据集含x个点，更新聚类中心的次数为n，将所有点聚为k簇，则传统K-means聚类方法的时间复杂度为O(x*n*k)[10-11]，安全区间更新优化K-means算法的时间复杂度为O(x/k*n)。相比传统K-means聚类算法，大数据集下，传统K-means的时间复杂度过高。优化算法在大数据量下，时间复杂度相对减少k2倍。

2 Spark的向量并行计算模型

基于Spark的K-means安全区间更新优化算法旨在优化大数据环境下的算法时间复杂度。传统K-means算法在每次迭代获取聚类中心后，需要全局迭代计算和比较数据集内的所有点与聚类中心的距离，以获取所有点的最新簇别。当数据集扩充到大数据环境下时，按照时间复杂度O(x*n*k)计算，其时间开销过高。尤其是大数据环境下容易陷入局部极值，此时，算法时间成倍增加，性能下降很快。

在改进K-means算法数据点簇别计算方式的基础上，基于Spark MLlib解决大数据量的并行迭代计算能力，提高数据点距离模型计算效率。在使用安全区间更新优化K-means聚类算法同时，通过Spark框架的并行计算能力和MLlib模块对向量集计算的优化机制，提高大数据集的K-means聚类计算效率。

2.1 Spark并行计算框架

Spark是一种融合了批处理、流处理、迭代式计算等独立分布式系统功能的并行计算框架。数据输入输出使用RDD(弹性分布式数据集，Resilient Distributed Datasets)抽象出横跨多个物理节点的数据集合，方便了并行的数据处理过程，改善了大数据环境下的并行计算效率[12-13]。Spark框架并行模型如图2所示。

图2 Spark框架并行模型

利用Spark框架在大数据分布式内存计算的优势，在Spark框架下实现优化的K-means算法，充分提高安全区间更新优化K-means算法在大数据下的并行执行效率。如图2所示，大数据集被存入分布式文件系统HDFS后，抽象成RDD数据模型，并分配到A/C中的多个物理节点，由多个计算引擎并行执行map和flatmap计算[14-15]，并将一轮聚类结果输入到不同RDD，并利用宽依赖进行RDD的转换。假设物理节点数为t，则该优化算法在Spark框架下的时间复杂度至少降低到O(x/k*n/t)。

同时，RDD模型在内存中转换，减少了磁盘IO的时间耗费。Spark MLlib模块优化了点到向量的计算模型，大量缩减了Spark上K-means安全区间更新优化算法的执行时间。

2.2 Spark MLlib点向量模型

使用Spark MLlib组件对K-means聚类算法进行了优化。在训练模型与预测模型两部分中，利用分布式MLlib向量均值计算，快速获取簇的聚类中心，避免陷入局部极值点，并使用内置误差平方和计算获取算法性能指标等。

使用Spark MLlib对K-means算法的优化基于向量数据模型(Vector)实现。向量和矩阵运算使用Breeze库的Vector/Matrix类型实现。计算中，Spark将分布式存放在不同节点上的聚类数据文件抽象成RDD模型，使用MLlib模块按行读取记录，将所有元素从文本数据转换为浮点数并map操作后形成新的RDD模型。RDD中每行记录作为数据点(a1,a2,…,an)被抽象为n维稠密向量模型。数据集中的点被抽象成空间向量进行聚类计算。由于Spark的并行计算特征，向量计算在Spark框架下存在更多的优势。

2.3 基于Spark的K-means安全区间更新优化算法

基于Spark的K-means安全区间更新优化算法，其并行化实现主要由Driver类、Mapper类、Combiner类以及Reducer类组成。算法流程如图3所示。

图3 基于Spark的K-means安全区间更新优化算法并行实现流程

Driver类初始化安全区间更新优化算法，通过setMapper(),setCombiner()和setReducer()驱动Mapper类、Combiner类和Reducer类，在相应类中实现map,combine和reducebykey操作函数对数据集进行处理。Spark MLlib通过textFile()将数据集作为一个RDD加载到Spark中，并用addFile函数拷贝共享数据到集群中的每个节点。Mapper类实现数据集的map过程，构建全局变量聚类中心点链表centerList，将数据集进行分类。通过map函数逐行扫描计算数据集中的数据对象RDD，将数据对象映射到对应的安全区间，最终输出键值对。其中key为数据对象，value为在该聚类中心所在聚类中的安全区间。迭代计算中间数据使用cache()函数转化为RDD。算法map过程伪代码如算法2所示。

算法2：基于Spark的K-means安全区间更新优化算法的并行map算法。

输入：

输出：

构建全局变量centerList，计算出初始centerList载入待处理数据集

for(Vectorscluster:centerList){

val distance=cluster.getV2().dist(value)

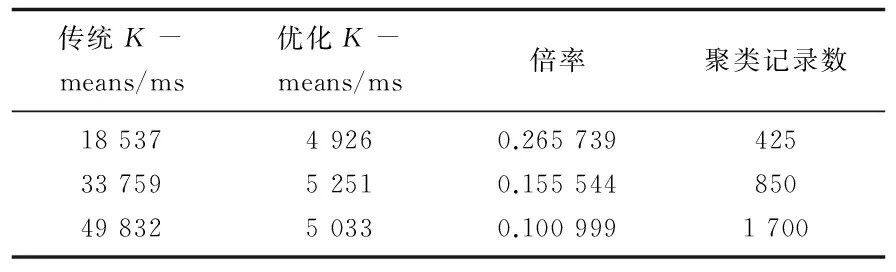
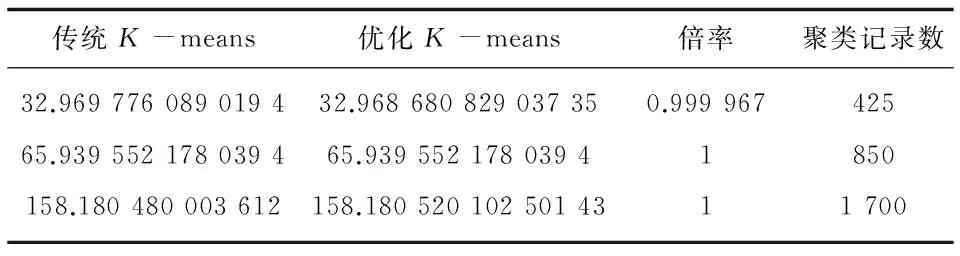
If(distance

min=distance;nearest_cluster=cluster. map(parseVector(_)).cache()

}}

key_new=nearest

clustercontext.write(key_new,value)

end

Combiner类实现RDD中间数据集的combine过程，数据集经过map过程后会生成大量RDD中间数据集，Spark平台为了不使网络通信成为瓶颈，会调用Combiner类在本地(同一节点)对属于同一key的value值求平均，精简得到局部结果后，再将数据传给主节点进行处理，减少通信量。Reducer类实现计算节点局部结果reduce的过程，汇总合并来自计算节点的combine过程局部结果，并用collect()函数将结果RDD以数组的形式返回生成全局结果。其中每个计算节点中combine的数据点数量不一，使用计数器对数据点进行统计，得出一个权值，在reduce计算时使用权值和局部结果计算得出全局结果。

K-means安全区间更新优化算法并行的reduce过程伪代码如算法3所示。

算法3：并行化的K-means安全区间更新优化算法的reduce算法。

输入：

输出：

初始化一个kmeans_Vector类型的average来存储新的中心点

for(kmeans_Vector v:value){

计算value均值，存在temp_average内}

将temp_average赋值给value_new

if(安全区间标签不小于0)

context.write(center,value_ new)

end

基于Spark MLlib组件的Vector向量模型和基础聚类功能，将要进行K-means安全区间更新优化聚类的大数据集加载到RDD，在多个物理工作节点上进行算法的并行计算，进一步提高算法的数据处理时间，适应于大数据下的使用场景。

3 实验与分析

实验使用数据来源于田间环境监测数据。环境传感器部署到江苏省农业科学院信息技术研究所的实验基地，采集观测点的光照，空气温湿度和土壤温湿度数据。数据以“编号|光照量|空气温度|空气湿度|土壤温度|土壤湿度|结束位”的形式实时上传到大数据中心，最终存入大数据仓库Hive进行分析处理。通过Spark框架将数据文件进行RDD抽象，加载为浮点数并规格化，基于MLlib模块的向量模型，把数据记录映射为空间点向量并进行聚类，分析误差等。实验把环境数据记录分为3类气象特征，并观测对应特征下的作物生长情况，以指导作物科学种植。

3.1 数据规格化

算法测试数据来源于环境传感器，每条环境数据记录被作为一个点向量，光照和温湿度被作为点向量的属性。使用误差评价函数作为算法性能指标。由于光照量、温湿度等指标的单位和数值相差较大，模型计算结果容易受到离群值和较大方差的特征影响。因此，在训练聚类模型之前，需要对特征属性进行归一化和标准化。通过对不同属性归一化，将数据保持在[0,1]之间进行精度控制，简化模型计算。

设某属性规格化之前为ai，规格化时考虑所有记录中该属性值的数值区间长度，并按式(5)对该属性进行规格化。

(5)

实验数据中共有5个环境属性值指标。其中，光照数值范围为0～10 000 Lux，空气和土壤温度数值范围为0℃～90 ℃，而空气和土壤湿度数值范围均为0%～100%。由于一条记录中存在5个不同属性数值范围和计算单位，在进行聚类时，数值范围较大的光照量会产生较大方差影响模型训练。将所有记录属性进行规格化处理，提高模型训练的准确性，避免离群值和较大方差属性的影响。

图4是原始环境记录和规格化后的对应结果。

图4 原始环境记录和规格化后的对应结果

3.2 效率评估分析

将图4规格化后的数据作为向量输入到基于Spark的K-means安全区间更新优化算法，进行聚类效果检测。使用平均误差准则函数和聚类完成的时间耗费作为聚类效果的评估依据。其中，平均误差准则是指每次选好中心点后进行的偏移量，数值大小与聚类效果成反比[16]，计算公式为：

(6)

其中，xi表示数据集中某点；ck表示该点所属类别的中心点。

这种计算点与聚类中心方差和的评估方法称为WCSS(Within_Cluster Sum of Squares)。

3.2.1 测试环境

使用Intel i7处理器，8 GB内存作为物理机，使用VMWare作为虚拟机搭建Spark集群，集群的操作系统使用Linux开源版本的CentOS。Spark框架使用Spark-1.4.0-Hadoop-2.6.0。Spark的数据源来自Hadoop的分布式文件系统模块HDFS进行文件存储。

Spark框架从集群角色上，将虚拟机分为负责作业调度的Nimbus和负责任务执行的Workers，分别使用一个VMWare虚拟机实现。算法数据计算基于Spark MLlib的SparkContext，创建分布式的RDD数据集，将HDFS上的传感器数据文件通过textFile()函数加载到内存中，跨越多个物理节点进行聚类运算。

3.2.2 算法实现

基于Spark的K-means安全区间更新优化算法将规格化后的环境数据记录抽象为包含光照、温湿度等属性的空间点向量，输入MLlib进行向量运算。算法使用Spark的MLlib模块作为向量运算的模型基础，通过并行计算向量属性，可以快速获取多个簇中集群的中心，避免了单机操作中串行的点计算过程。此外，MLlib提供了快速计算平均误差准则WCSS的API，优化了向量计算的底层数据模型，相比单机下使用Java等模型或普通浮点数模型计算效率更高。将环境数据无监督地聚为3簇，以用于归纳不同气象特征的数据，研究对应的作物生长状态。

3.2.3 结果分析

从直观的聚类结果图可以发现，原始环境数据的簇别被设置为0。改进K-means算法和传统K-means算法相比，聚类准确性方面，主要在于将传统K-means算法簇0的记录表现为簇1和簇2。偏差记录数量较少，绝大部分数据记录线重合，表明改进K-means算法对聚类准确性影响较小。

如表1和表2所示，基于Spark的K-means安全区间更新优化算法在平均误差准则上，随着聚类记录数快速增加，其变化较小。表明优化K-means算法在聚类效果上与传统K-means算法有相似的准确性。

表1 传统K-means和优化K-means下的算法时间性能

如表1和表2所示，在记录数为425，850和1 700条时，优化算法时间耗费分别占传统K-means的26.6%，15.6%和10%。因此，提出的基于Spark的K-means安全区间更新优化算法与传统K-means算法相比，在聚类准确性和聚类效果上，具有基本相似的聚类效果。在时间耗费上，具有明显的时间优势，且随着数据量增大，时间优势更加明显。

表2 传统K-means和优化K-means下的聚类性能对比

4 结束语

为了解决大数据环境下K-means时间复杂度过大的问题，提出了基于Spark的K-means安全区间更新优化算法。与传统K-means算法相比，该算法避免了全局迭代计算点与聚类中心的距离，而将所有的点映射到安全区间，每次更新聚类中心后只需更新安全区间的标签即可更新区间内所有点的簇别，提高了聚类时全局的距离迭代计算效率，减少了时间复杂度。利用Spark的MLlib组件的向量并行计算模型，对大数据集进行RDD分布式数据处理，加快了算法对数据的处理时间。调用MLlib的WCSS函数和向量簇中心API，快速实现簇内计算。实验结果表明，随着传感器数据量的快速增加，优化算法保证了聚类准确性并具有明显的时间优势。

[1] 吴夙慧,成 颖,郑彦宁,等.K-means算法研究综述[J].现代图书情报技术,2011(5):28-35.

[2] 李 梓,于海涛,贾美娟.基于改进模拟退火的优化K-means算法[J].计算机工程与应用,2012,48(24):77-80.

[3] 袁 方,周志勇,宋 鑫.初始聚类中心优化的k-means算法[J].计算机工程,2007,33(3):65-66.

[4] 谢娟英,王艳娥.最小方差优化初始聚类中心的K-means算法[J].计算机工程,2014,40(8):205-211.

[5] 海 沫,张书云,马燕林.分布式环境中聚类问题算法研究综述[J].计算机应用研究,2013,30(9):2561-2564.

[6] 赵卫中,马慧芳,傅燕翔,等.基于云计算平台Hadoop的并行k-means聚类算法设计研究[J].计算机科学,2011,38(10):166-168.

[7] 徐新瑞,孟彩霞,周 雯,等.一种基于Spark时效化协同过滤推荐算法[J].计算机技术与发展,2015,25(6):48-55.

[8] 虞倩倩,戴月明,李晶晶.基于MapReduce的ACO-K-means并行聚类算法[J].计算机工程与应用,2013,49(16):117-120.

[9] Poteras C M,Mihaescu M C,Mocanu M.An optimized version of the K-Means clustering algorithm[C]//Computer science and information systems.[s.l.]:IEEE,2014:695-699.

[10] Brusco M J,Cradit J D.A variable-selection heuristic for k-means clustering[J].Psychometrika,2001,66(2):249-270.

[11] 张雪凤,张桂珍,刘 鹏.基于聚类准则函数的改进K-means算法[J].计算机工程与应用,2011,47(11):123-127.

[12] 陈侨安,李 峰,曹 越,等.基于运行数据分析的Spark任务参数优化[J].计算机工程与科学,2016,38(1):11-19.

[13] 梁 彦.基于分布式平台Spark和YARN的数据挖掘算法的并行化研究[D].广州:中山大学,2014.

[14] 吴哲夫,张 彤,肖 鹰.基于Spark平台的K-means聚类算法改进及并行化实现[J].互联网天地,2016(1):44-50.

[15] Gopalani S,Arora R.Comparing apache spark and map reduce with performance analysis using k-means[J].International Journal of Computer Applications,2015,113(1):8-11.

[16] 韩凌波,王 强,蒋正锋,等.一种改进的k-means初始聚类中心选取算法[J].计算机工程与应用,2010,46(17):150-152.

Optimization ofK-means Updating Security Interval Based on Spark

LI Yu-bo1，YANG Yu-wang1，TANG Hao1，CHEN Guang-wei2

(1.School of Computer Science and Engineering,Nanjing University of Science and Technology,Nanjing 210094,China；2.Purdue University,West Lafayette 47906,USA)

At each time when theK-means algorithm updates the cluster center,it needs to calculate iteratively the distance between all the points in the dataset with the latest clustering center to get the latest clustering of each point.This feature of global iterative computation leads to low efficiency of traditionalK-means algorithm.As the data set increases,its time efficiency and clustering performance decrease too fast,so that the traditionalK-means algorithm is not suitable for clustering in big data.Therefore,a newK-means secure interval updating algorithm based on Spark is proposed for time efficiency and performance optimization in big data.After updated the cluster center every time,it updates security interval label.According to whether the label is greater than 0 instead of calculation of the distance between all the points and the new center and cluster identification of all the data in the interval every time,which reduces the overhead of time and computation.The performance of the algorithm model based on the point vector model of Spark MLlib component has been optimized.It is made a comparison with the traditionalK-means algorithm on average error criterion and operation time.The experimental results show that it is superior to the traditionalK-means clustering algorithm in the above two indexes and is suitable for data clustering scenario in big data.

K-means;security interval;Spark;big data;time efficiency

2016-09-29

2016-12-29 网络出版时间：2017-07-05

江苏省农业科技自主创新资金项目(CX(16)1006)

李玉波(1991-)，男，硕士研究生，研究方向为大数据应用；杨余旺，博士，教授，博士生导师，研究方向为网络编码、大数据应用。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1652.072.html

TP301

A

1673-629X(2017)08-0001-06

10.3969/j.issn.1673-629X.2017.08.001