基于同类测试样本组的稀疏表示人脸识别

谢尚高，王丽平

(南京航空航天大学 理学院，江苏 南京 210016)

基于同类测试样本组的稀疏表示人脸识别

谢尚高，王丽平

(南京航空航天大学 理学院，江苏 南京 210016)

近年来的研究表明，稀疏表示分类(SRC)方法是一种有效的人脸识别方法。SRC是单个样本基于向量l1-范数正则化的最小二乘分类。但现实中常常存在着已知多个测试样本属于同一类的情况，无疑有利于分类，而基于SRC或其他单样本模型的方法却未能利用该信息。为利用类别标签信息，提出了一种新的鲁棒人脸识别方法。该方法基于同类测试样本组的稀疏表示分类(IGSRC)，即将同类多个测试样本放至同组，采用矩阵L1-范数正则化的最小二乘分类进行稀疏表示，将测试样本组判为类别中残差最小的标号。实验结果表明，相比于SRC与IGSRC方法，所提出的方法不但能取得更高的人脸识别率(即使在每类别训练样本数较少、训练样本存在部分遮挡)，而且具有更少的计算耗时。

类内测试样本组；稀疏表示；人脸识别；矩阵L1-范数；多样本

0 引 言

人脸识别是指对未分类的人脸样本从众多人脸中判别出类别。人脸识别一直是计算机视觉、模式识别等领域的研究热点，主要集中在两部分：一是人脸特征的选取，二是分类器的构造。在人脸特征选取方面，早期的方法主要考虑人脸几何特征，后期则从统计学习的角度出发，有了更进一步的发展，包括基于主成分分析的特征脸[1]、应用线性判别分析的Fisher脸[2]、基于局部特征的提取方法(如Gabor小波法[3-4]、LBP[5]方法)等。在分类器方面，线性分类器使用最多，如最近邻(Nearest Neighbor)[6]、最近特征线(Nearest Feature Line)[7]、最近子空间平面(Nearest Subspace Plane)[8-10]等。

随着压缩感知理论[11-13]的发展，J.Wright等[14]提出用于人脸识别的稀疏表示分类(Sparse Representation-based Classification，SRC)方法，并在数值实验上证明该方法的识别准确率和鲁棒性都有所提升。SRC提出单个测试样本可以用所有类别的训练样本进行线性表示，它通过l1-范数最小化自动寻找最稀疏的线性表示，大部分非零因子应集中在正确的类别上，从而自动满足寻找正确类别的过程。稀疏表示具有很好的鲁棒性[15-16]，后续对SRC算法的改进及拓展包括CRC[17]、ESRC[18]、PCRC[19]等。其中CRC认为SRC在识别中起主要作用的是协同表示，而非稀疏优化，所以CRC采用l2-范数最小化取得了和SRC类似的表现，但识别速度更快；ESRC则加强了对字典的学习，加入类内差异与原训练样本集组成新的训练字典。

SRC及拓展方法都只考虑单个测试样本的表示与分类，而单个人脸样本因为表情、光照、遮挡等因素具有较大的随机性，有时同类之间也有较大的差异性，甚至存在类内差异大于类间差异的情况，而在许多应用场景中，同类的待识别样本往往有多个，单个样本逐一识别没有充分利用这些待识别样本属于同类这一先验知识。

针对该问题，考虑基于多样本的同类测试样本组的稀疏表示分类(Sparse Representation Classification with Intra-class testing-sample Group，IGSRC)，将测试样本中已知属于同类的放至同组，对该组测试样本进行矩阵L1-范数正则化的最小二乘(Frobenius范数)表示，通过ADMM(Alternating Direction Method of Multipliers)优化求解得表示系数后，计算对应的各个类别的重构残差，将该组测试样本判别为最小残差的类别,并通过实验进行验证。

1 稀疏表示分类

SRC将人脸识别模型表述成如下l1-范数最小化问题：

(1)

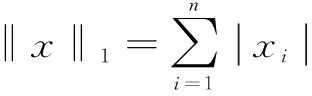
(2)

2 基于同类测试样本组的稀疏表示分类

(3)

2.1 系数表示

(4)

进一步展开，即：

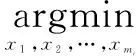
(5)

于是可以拆分成如下mi个子向量l1-范数最小化进行：

(6)

2.2 分 类

(7)

总结以上过程，即为：

算法1：基于同类测试样本组的稀疏表示分类(IGSRC)。

(1)输入：给定同类测试样本组Yi∈Rd×mi,c类训练样本集A=[v1,1,v1,2,…,vc,1,…,vc,nc]∈Rd×n，正则化参数λ。

(2)单位化A、Yi的列向量，使其具有l2-范数单位长度。

(3)求解以下矩阵L1-范数最小化问题：

(3)防治工程坡体岩体工程地质特征。强风化片麻岩黏聚力0 MPa，内摩擦角35°，容重21 kN/m3，承载力特征值为300 kPa。根据取样试验，强风化片麻岩天然单轴抗压强度为28.6～38.2 MPa，饱和抗压强度为19.1 MPa；中风化片麻岩天然单轴抗压强度为109.0～113.0 MPa，饱和抗压强度为92.3 MPa。

(8)

(4)计算残差rj(Yi)=‖Yi-Aδj(X*)‖F,j=1,2,…,c。

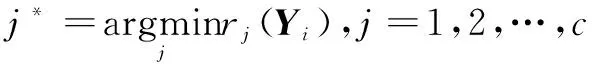
3 数值实验

利用公开数据库对算法IGSRC和SRC进行比较，选择各自实验效果最佳的参数λ，报告实验结果。对于SRC模型的l1-范数最小化，文献[14]给出的算法[20-21]是化为二阶锥规划利用牛顿迭代求解(下面简称L1QC)，同时采用速度更快的l1-范数最小化算法-ADMM[22]，所以同时比较上述两种优化方法得到的结果，对应的SRC模型分别称之为SRC(L1QC)、SRC(ADMM)，而对于算法IGSRC，采用ADMM算法求解式(6)。

3.1 无遮挡人脸识别

3.1.1 AR数据库

选择AR数据库[23]常用的子版本，包含50个男性和50个女性在光照变化、表情变化、有无遮挡下的每人26张165×120维面部图像，将其分成两部分：session1和session2，每部分每人包含7张无遮挡图像、3张墨镜遮挡、3张围巾遮挡，共计13张图像，如图1所示。记数据库中第1个男性为类别1，第2个男性为类别2……第1个女性为类别51，依此类推，共100类。选择每人只有光照、表情变化的14张图像进行无遮挡数值实验，即将来自session1的前7张作为训练样本，session2的前7张作为测试样本。将每张图像转化成灰度矩阵，同文献[14]的采样方式，将图像裁剪成4个特征维数：30、54、130、540，对应于采样率1/24、1/18、1/12、1/6，并下拉成向量，进行向量l2-范数单位化。

图1 AR数据库单个人的所有样本

实验结果如图2(a)所示。

3.1.2 Extended Yale B数据库

Extended Yale B数据库[24]包含38个人每人约64张共计2 414张人脸图像。图像是在实验室控制下的光照变化得到的，像素是192×168维。同样，将每张图像转化为灰度矩阵，同文献[14]的采样方式，将图像裁剪成30、56、120、504维，并下拉成列向量和进行l2-范数单位化，随机取每个人约一半的图像作为训练集，剩下的为测试集，得到的结果如图2(b)所示。

图2 IGSRC和SRC在AR与Extended Yale B上的识别率

由图2(b)可见，IGSRC的识别率仍然在所有维数中表现最好，尤其在低维(30、56维)时超过SRC方法10%，在56维及以上取得了100%的识别率。因为Extended Yale B较AR样本类别数少且样本个数多，类似的维数下识别率比AR高也是意料之中。

3.2 更少训练样本数的人脸识别

减少训练集每类样本数量以测试算法的性能。在AR数据库选择无遮挡人脸图像，训练样本从之前的每个人7张图像以1张递减逐步减少到1张，而测试集与之前一致，仍为每人7张图像。所有实验图像都采样成540维，其他处理方式同3.1.1。

表1显示了当每个人的训练样本数为1～6时10次随机置换训练样本后识别率的均值和相对标准差。在每人训练样本数为2个及以上，IGSRC都取得了较高的识别率均值(90%以上)，相对标准差只有对应的SRC方法的1/6～1/3，SRC在训练样本数低于4时识别率均值已不足80%。表明IGSRC较SRC的识别率和稳定性更佳。而在每人训练样本数为1时，两种方法表现都欠佳。

表1 在AR数据库上不同的训练样本数下的识别率

3.3 有遮挡人脸识别

为了测试IGSRC的鲁棒性，将AR数据库中包含遮挡的人脸图像纳入进行数值实验。(1)全混合：选择session1中100个人每人13张图像(包含6张遮挡图像，其中3张佩戴墨镜、3张佩戴围巾，见图1)作为训练集，选择session2中所有13图像(包含6张遮挡)作为测试集。(2)半混合：选择session1的100个人每人7张无遮挡图像作为训练集，session2中每人所有13张图像(包含6张遮挡)作为测试集。(3)无混合：选择session1的100个人每人7张无遮挡图像作为训练集，session2中每人6张遮挡图像作为测试集。这三种选择使得识别任务的挑战性逐步增大，训练集中从所有样本到仅有无遮挡图像，测试集从所有样本到仅有遮挡图像。所有实验图像都采样成540维，其他处理方式同3.1.1。具体的数值实验结果如表2所示。

在3种混合选择中，IGSRC依然比SRC在识别率上的表现更好，在“全混合”和“半混合”中，IGSRC基本不受遮挡影响，识别率高达96%以上。而在条件最严苛的“无混合”中，IGSRC的识别率为66%，仍然远高于SRC(36.17%)。说明在训练样本和测试样本中存在相同“类型”(同含有遮挡或无遮挡)时，IGSRC的鲁棒性较高。

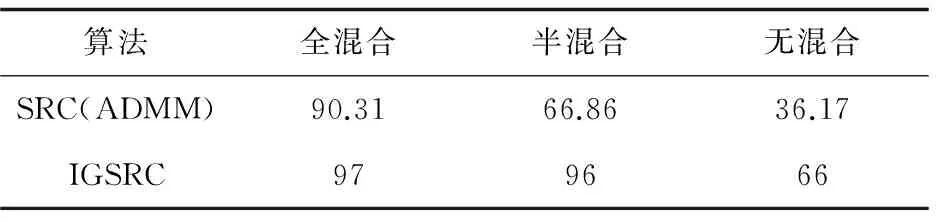
表2 在AR数据库有遮挡下的识别率 %

3.4 时间对比

SRC是对单个测试样本逐一进行系数表示、分类，IGSRC是基于同类测试样本组进行整体表示、整体分类，如果训练样本数量和同组测试样本数量越多，IGSRC理应会有更低的识别(系数表示+分类)时间。在Intel(R) Core (TM) i5-2400 3.10 GHz CPU, 4 GB RAM的个人电脑Matlab R2012b上，按3.1.1与3.1.2无遮挡的选择方式(其中仅选择AR数据库图像维数为540维，Extended Yale B图像维数为504维)，计算IGSRC和SRC对所有测试样本(AR数据库700个，Extended Yale B约1 200个)的识别时间，实验重复进行10次，结果取均值与相对标准差，如表3所示。

表3 在AR和Extended Yale B上对所有测试样本的识别时间 s

由表3可见，IGSRC比SRC具有更佳的识别时间及稳定性，同时在Extended Yale B中由于测试样本组中包含的样本数(约32个)比AR测试样本组包含样本数(7个)更多，较SRC的时间优势体现得更明显，对约1 200个测试样本识别时间提升10 s左右。

4 结束语

SRC及其改进方法基本上是基于单样本进行表示分类。而在许多应用场景中，同类的测试样本往往有多个。为充分利用这一信息，采用IGSRC对人脸进行识别，将已知同类测试样本分至一组，通过矩阵L1-范数整体系数表示和整体分类，使得一些单样本的类内较大差异被类内较小差异的样本所弥补，因而IGSRC算法获得了比基于向量l1-范数的SRC更高的识别率、鲁棒性和更低的相对标准差。同时，IGSRC较SRC计算耗时更低。但是，IGSRC对测试样本组内的测试样本“质量”要求较高，若算法中类内差异较大的样本造成的影响大于类内较小差异的样本，则整个测试样本组将被判错，但能容纳类内差异较大样本也是IGSRC的优势，如何平衡二者的影响，是进一步研究的方向。

[1] Turk M A,Pentland A P.Face recognition using eigenface[C]//Proceedings of IEEE conference on computer vision & pattern recognition.[s.l.]:IEEE,2011.

[2] Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs. fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,1997,19(7):711-720.

[3] Lades M,Vorbruggen J C,Buhmann J,et al.Distortion invariant object recognition in the dynamic link architecture[J].IEEE Transactions on Computers,1993,42(3):300-311.

[4] Liu C.Capitalize on dimensionality increasing techniques for improving face recognition grand challenge performance[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2006,28(5):725-737.

[5] Ahonen T,Hadid A,Pietikäinen M.Face recognition with local binary patterns[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2006,28(12):2037-2041.

[6] Duda R O,Hart P E,Stork D G.Pattern classification[M].[s.l.]:John Wiley & Sons,2012.

[7] Li S Z,Lu J.Face recognition using the nearest feature line method[J].IEEE Transactions on Neural Networks,1999,10(2):439-443.

[8] Chien J T,Wu C C.Discriminant waveletfaces and nearest feature classifiers for face recognition[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2002,24(12):1644-1649.

[9] Ho J,Yang M H,Lim J,et al.Clustering appearances of objects under varying illumination conditions[C]//IEEE computer society conference on computer vision and pattern recognition.[s.l.]:IEEE,2003.

[10] Lee K C,Ho J,Kriegman D J.Acquiring linear subspaces for face recognition under variable lighting[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2005,27(5):684-698.

[11] Donoho D L.For most large underdetermined systems of linear equations the minimal L1-norm solution is also the sparsest solution[J].Communications on Pure & Applied Mathematics,2007,59(6):797-829.

[12] Candès E J,Romberg J K,Tao T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure & Applied Mathematics,2006,59(8):1207-1223.

[13] Candès E J,Tao T.Near-optimal signal recovery from random projections:universal encoding strategies?[J].IEEE Transactions on Information Theory,2007,52(12):5406-5425.

[14] Wright J,Yang A Y,Ganesh A,et al.Robust face recognition via sparse representation[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2008,31(2):210-227.

[15] 闫德勤,刘胜蓝,李燕燕.一种基于稀疏嵌入分析的降维方法[J].自动化学报,2011,37(11):1306-1312.

[16] 胡正平,宋淑芬.基于类别相关近邻子空间的最大似然稀疏表示鲁棒图像识别算法[J].自动化学报,2012,38(9):1420-1427.

[17] Zhang L,Yang M,Feng X.Sparse representation or collaborative representation:which helps face recognition?[C]//International conference on computer vision.[s.l.]:IEEE Computer Society,2011:471-478.

[18] Deng W,Hu J,Guo J.Extended SRC:undersampled face recognition via intraclass variant dictionary[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2012,34(9):1864-1870.

[19] Cai S,Zhang L,Zuo W,et al.A probabilistic collaborative representation based approach for pattern classification[C]//IEEE conference on computer vision and pattern recognition.[s.l.]:IEEE,2016.

[20] Boyd S,Vandenberghe L.Convex optimization[M].[s.l.]:Cambridge Univ. Press,2004.

[21] Candès E,Romberg J.l1-magic:recovery of sparse signals via convex programming[R].[s.l.]:[s.n.],2005.

[22] Boyd S,Parikh N,Chu E,et al.Distributed optimization and statistical learning via the alternating direction method of multipliers[J].Foundations & Trends® in Machine Learning,2011,3(1):1-122.

[23] Martinez A R,Benavente R.The AR face database[R].[s.l.]:[s.n.],1998.

[24] Georghiades A S,Belhumeur P N,Kriegman D J.From few to many:illumination cone models for face recognition under variable lighting and pose[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2001,23(6):643-660.

Sparse Representation Classification for Face Recognition with Intra-class Testing-sample Group

XIE Shang-gao，WANG Li-ping

(College of Science,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

Recent studies have shown that Sparse Representation Classification (SRC) is an effective method for face recognition.SRC is a least squares classification based onl1-norm regularized for a single testing-sample.However,in the case that multiple testing-samples are known to be the same class which is surely helpful in the classification,the common-class label information is not included in SRC or other single-sample models.Therefore,a novel robust face recognition method based on sparse representation classification is proposed which is on the basis of IGSRC.Taking multiple intra-class testing-samples into the same group,it adopts the matrixL1-norm regularized least squares classification for sparse representation and judges the test sample group as the label with minimum error in classes.Experimental results show that compared with IRC and IGSRC,the method proposed cannot only obtain better face recognition rate (even when the number of training samples per subject is small or training samples are partly occluded),also own less running time.

intra-class testing-samples;sparse representation;face recognition;matrixL1-norm;multiple samples

2016-08-03

2016-11-08 网络出版时间：2017-07-05

国家自然科学基金资助项目(11471159,61661136001)；南京航空航天大学研究生创新开放基金(kfjj20150706)

谢尚高(1989-)，男，硕士研究生，研究方向为最优化算法及其应用；王丽平，副教授，研究方向为最优化理论与方法及应用。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1650.028.html

TP301

A

1673-629X(2017)08-0007-05

10.3969/j.issn.1673-629X.2017.08.002