基于改进合作协同进化算法PID整定

梅 领，罗 杰

(南京邮电大学 自动化学院，江苏 南京 210046)

基于改进合作协同进化算法PID整定

梅 领，罗 杰

(南京邮电大学 自动化学院，江苏 南京 210046)

针对复杂系统PID控制的参数整定问题，为在给定性能指标下实现PID三个参数以协同进化方式自动搜索的最佳组合，提出了一种基于改进合作协同进化的PID控制器参数优化方法。该方法根据PID控制器模型，设计了更具有针对性的PID参数优化目标函数，结合协同进化算法对参数进行最优组合，并在合作协同进化算法的基础上，提出了PID参数协同进化之前执行分组排序策略，依据处理结果选择确定最优组作为下一代协同进化的代表组合，根据代表组合评估分组排序优劣。仿真结果表明，所提出的新型合作协同进化算法应用于PID参数相比传统的进化算法具有更好的优化效果，且算法的收敛速度快、自适应性强、精确度高，显现出较好的应用前景。

PID参数整定;协同进化;排序策略;优化目标函数

0 引 言

PID控制是最早发展起来的控制策略之一，由于算法简单、鲁棒性和可靠性好，在过程控制和运动控制中应用广泛，例如轧钢机[1]、直流电机控制[2]和回转液压系统[3]等。然而在实际的工业生产过程中往往具有非线性、时变不确定性，因此很难建立精确的数学模型[4]。PID控制性能与其参数整定存在着直接的关系，传统的PID参数采用Z-N方法[5-6]进行整定，这是经验试凑的方法。近些年，一些启发式算法相继提出，用来对PID参数进行整定优化。这些算法尝试着在搜索空间中找到目标问题的最优结果，如遗传算法(GA)[7]、模拟退火算法(SA)[8]和粒子群算法(PSO)[9-11]等，在PID控制参数优化中得到了成功应用。Lin等在2009年使用遗传算法优化PID参数在直流电机控制领域[12]的应用，Dashti J M等在2010年改进了模拟算法在数字PID控制器整定方面[13]的应用。Nangru D等在2013年改进PSO算法在PID整定稳定过渡过程中的应用[14]。

上述算法都是在独立的解空间中进行寻优，对于目标解搜索的效果并不是很好。GA很容易陷入局部最优值，SA的收敛速度又很慢，PSO也存在上述一样的缺陷。为了避免寻优在相对独立的解空间中进行搜索，导致对于PID控制器参数整定优化的程度较差，提出PID待优化参数之间采用协同进化的策略对解空间进行组合式寻优。

协同进化[15]是近年来针对启发性搜索算法的不足而兴起的一个研究热点，指的是多个种群通过适应值的关联性同时进化。协同进化算法是在传统进化算法的基础上引入生态系统(ECO system)的概念，传统进化算法常常将待求解问题映射为单一种群的进化，而协同进化算法将待求解问题映射为相互作用的各物种组成的生态系统，以生态系统的进化来达到问题求解的目的[16]。为此，基于该算法，提出了一种新型的合作协同进化算法应用于控制系统PID参数整定并对该算法进行实验验证。

1 PID控制系统参数整定基本原理

PID控制是一种线性控制方法，根据给定的r(t)与实际输出值y(t)构成控制偏差e(t)，即e(t)=r(t)-y(t)。对偏差e(t)进行比例、积分、微分运算，将三种运算结果相加，就得到PID控制器的控制输出u(t)。在连续时间域中，PID控制器算法[17]表达如下：

(1)

其中，kp为比例系数；ki为积分系数；kd为微分系数。

所谓PID参数整定，指的是通过某种确定的算法寻找一组最优参数，使得PID调节达到减少超调量、减少上升时间和获得最好稳定时间的要求。PID控制器各校正环节作用如下：

(1)比例环节：成比例地反映控制系统的偏差信号e(t)，偏差一旦产生，控制器立即产生控制作用以减小偏差。

(2)积分环节：主要用于消除静差，积分作用的强弱取决于积分系数，系数越小，积分作用越弱，反之则越强。

(3)微分环节：反映偏差信号的变化速率，能在偏差信号变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。

常见的优化目标函数J有三种：

ITAE:

(2)

IAE：

(3)

ITSE：

(4)

这些优化目标函数并没有包含显式的系统相关性能指标，如上升时间tr、超调量δ%、调节时间tf等。

为了防止PID控制器的输出量u过大、获得较小的上升时间tr及较小的调节时间tf，可以取目标函数形式如下(以上述IAE为例)：

(5)

其中，w1,w2,w3为权值。

(6)

最后，系统的优化问题可表述为(设最小值为最优解)：

(7)

2 合作协同进化算法

合作型的协同进化算法,是将复杂系统的优化问题分解为一系列子系统的优化问题，各子系统可分别进行优化，再从整体上进行协调。子系统的优化和整体协调的过程往往需要交替迭代进行，直到找到优化问题的解。合作型协同进化算法就是采用类似的思想来处理复杂问题的演化。

合作型协同进化的基本思想是：首先将待优化复杂系统变量分组，转化为多个少变量系统优化问题；然后对多个变量系统分别编码，形成多个独立的子种群，各个子种群独立进化，因为单个子种群的个体仅代表复杂系统的一个部分，故个体进行适应度评估时必须用到其他子种群的个体信息，称为代表个体，即待优化系统的完整解由个体种群中的代表个体组成，各个子种群只有相互合作才能完成优化任务，通常选择当前种群最优个体为代表个体。

研究发现，在合作协同进化的基础上提出在协同组合进化之前先进行组合评估，选择出当前种群组合最优的代表个体，这些代表个体评估各子种群的适应度，种群间合作协同进化，这样的进化方式，能更有效地找到最优的组合解。将这种协同进化方式运用到PID参数整定中，会较好地优化PID整定效果。为了研究如何提高合作型协同进化算法的搜索效率，并且更好地适用于PID控制器参数整定，提出了在协同交互之前对种群组合进行优化筛选，利用选出的最优组合作为代表个体在种群之间进行协同进化，经过不断的搜索达到最优效果。函数优化实例和PID控制器的仿真实验验证了该算法的有效性。

针对现有算法优化的不足，提出这种合作型协同进化算法应用于控制系统PID参数整定，所提算法得到了PID控制参数更理想的组合，并达到了理想的控制优化效果。建立优化控制系统，分为三大块，分别是：改进型协同进化优化模块、PID控制系统和控制效果评估。

图1为基于协同进化的PID参数优化系统结构。其中EA1、EA2、EA3为三个进化算法模块。

3 改进型协同进化

3.1 协同优化模块

种群P1、P2和P3分别代表参数kp、ki和kd，种群规模为n，将所有种群中的个体按编号分组，代入目标问题(Domain model)中并评估相应的适应度值，选取适应度值最好的组合，作为评估代表组(Xbest,Ybest,Zbest)。若满足进化的终止条件，则当前种群中最优协作评估代表组就作为问题的最优协同解，终止计算。反之选择当前最优组合作为评估代表组，继续引导下一代种群进化。

各个种群个体Pi,j(i=1,2,3)适应度评估，由评估代表组(Xbest,Ybest,Zbest)协同完成。如：种群P1个体P1,j(j=1,2,…,n)的适应度评估是由(P1,j,Ybest,Zbest)代入到目标问题进行评估，得到其对应个体的适应度值P1,j，并将其中适应度高于当前评估代表组组合中的P1,j替换Xbest。

各个种群个体评估后，根据各个种群中每个个体的适应度值，所有种群各自进化，选择合适的进化算法，该进化算法根据种群个体的适应度进行进化操作,如遗传算法的选择、交叉、变异等操作。EA1、EA2和EA3可以相同也可以不同，进化后得到新一代种群。

3.2 算法步骤

(1)初始化。

初始化种群P1(0),P2(0),P3(0)；置进化代数计数器初值m：=0；设定进化终止准则。

(2)选评估代表组。

选取种群个体(P1,j(m),P2,j(m),P3,j(m)),j=1,2,…,n，组成待选组，评估计算每组的适应度值，选出当前适应度值最好的一组作为评估代表组：(Xbest,Ybest,Zbest)。

(3)终止判断。

如果满足进化终止条件，则当前评估代表组(Xbest,Ybest,Zbest)就作为问题的最优协同解，终止计算。

(4)各个种群个体适应度值的评估。

如图2所示，种群P1中的个体适应度评估，由评估代表组参与协作，将(P1,j,Ybest,Zbest)代入目标问题中进行评估，得到对应的适应度值，并将其中适应度高于当前评估代表组组合中的P1,j替换Xbest。

(5)各个种群分别进化。

将所有种群中每个个体的适应度值评估完后，各个种群采用选择算子、交叉算子、变异算子等进化操作，各自进行进化，产生新一代种群P1,j(m+1),P2,j(m+1),P3,j(m+1)；置m：=m+1,转步骤(2)。

4 改进型协同PID算法

4.1 初始化种群

参数kp、ki、kd的对应种群分别为P1、P2、P3，种群规模为n，将参数对应的种群初始化为种群P1(0),P2(0),P3(0)，进化代数计数器为m:m=0，设定种群进化的终止条件，如种群进化到第q代，则停止进化。

4.2 评估代表组的选取

选取所有种群中的个体组成待选组：(P1,j(m),P2,j(m),P3,j(m))(j=1,2,…,n)。将待选组代入目标问题进行适应度评估。由图1所知，PID控制器系统与控制效果评估两部分组合在一起，作为目标问题，控制效果评估采用式(1)作为目标函数J，将待选组代入到PID控制器。PID控制器的作用是：使给定yd(t)与实际输出y(t)的误差e(t)趋近于零。

PID控制器根据待选组输入(如图2所示)，输出控制量u(t)，控制量整定被控对象G(s)，输出对应的实际输出y(t)。PID控制器系统每完成一次参数整定操作，就产生对应的响应曲线(反映系统的性能指标)，响应曲线中提取上升时间tr的值，在一定的调节时间tf内，把响应曲线离散化成一些点，然后在响应曲线的峰值的10%和90%两处相减得到tr。这时在PID控制系统中得到对应的量：调节时间tf，上升时间tr，误差值e(t)，控制量u(t)，将这些对应的量代入到控制效果评估模型中，利用目标函数J计算对应的适应度值，并选取适应度值最好的组合作为评估代表组(Xbest,Ybest,Zbest)。判断种群进化终止条件，若满足终止条件，则当前评估代表组(Xbest,Ybest,Zbest)就作为问题的最优协同解，终止计算。

4.3 个体适应度评估

对所有种群中个体Pi,j(i=1,2,3)进行适应度评估，如：种群P1中的个体P1,j，由评估代表组(Xbest,Ybest,Zbest)参与协作，将(P1,j,Ybest,Zbest)代入PID控制器，在PID控制器系统中产生相应的量：调节时间tf，上升时间tr，误差值e(t)，控制量u(t)，将这些对应的量代入到控制效果评估模型中的目标函数J，计算对应的适应度值，并将其中适应度高于当前评估代表组组合中的P1,j替换Xbest。

4.4 各个种群分别进化

各种群中所有个体评估后，根据各个种群中每个个体的适应度值，所有种群各自进化，选择合适的进化算法。该进化算法根据种群个体的适应度进行进化操作，如遗传算法的选择、交叉、变异等操作。EA1、EA2和EA3可以相同也可以不同，进化后得到新一代种群P1,j(m+1)，P2,j(m+1)和P3,j(m+1)，置m：=m+1。

改进型协同PID算法流程图如图2所示。

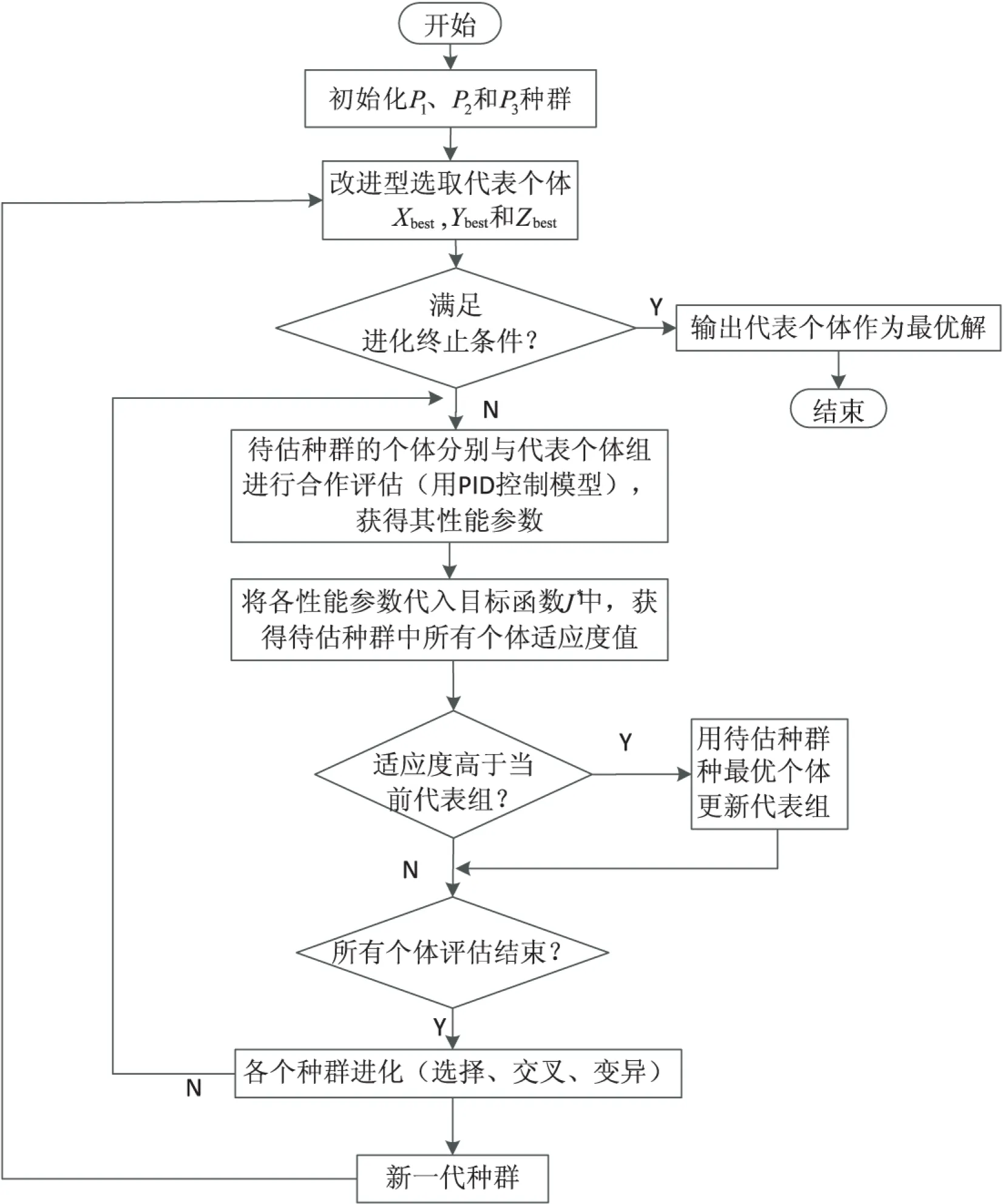
图2 改进型协同PID算法流程

5 实验验证

5.1 算法验证

为了验证改进的协同进化算法相对于其他启发式算法在种群交互进化上的不同，研究发现将改进协同进化算法中的进化算法模块，用遗传算法替代，将更容易比较对目标函数优化方面的改进。选出几种常见的测试函数，如表1所示。

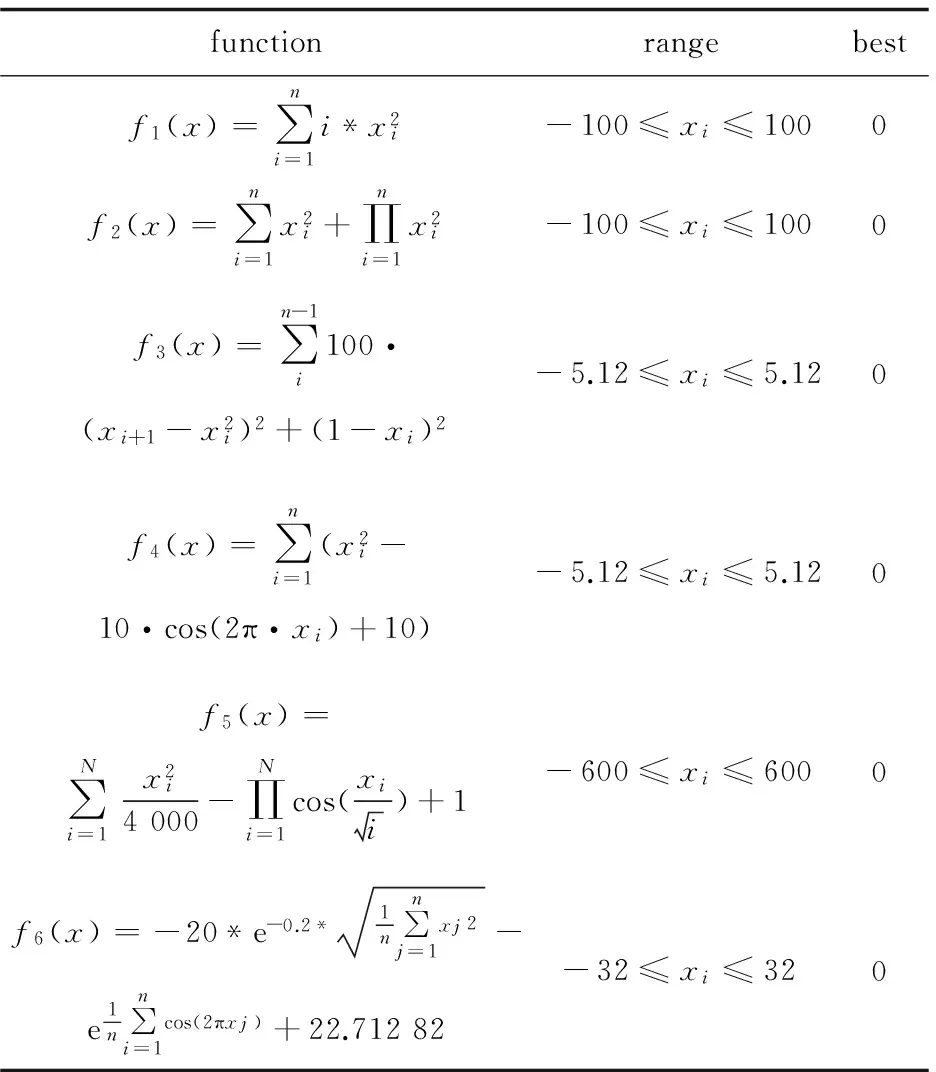
表1 测试函数

研究目的是将改进协同进化算法应用到PID整定中，所以在以下的测试函数中选定变量维度为3，为保证算法的公平性，统一定义种群规模50，进化代数200，运行次数100，将100次的计算结果求平均，消除算法本身的偶然性。粒子群算法取W(惯性权值)为0.729 8，C1,C2(加速因子)都取2。遗传算法交叉概率Pc取0.8，变异概率Pm取0.1，差分算法中交叉因子取0.5，交叉概率CR取0.8；合作协同进化算法中遗传算法部分的交叉概率取0.8，变异概率取0.1；改进协同进化算法中算法模块采用遗传策略，其中交叉概率0.8，变异概率0.1。

改进协同进化算法与其他4种进化算法，分别对测试函数f1～f6进行优化。已知测试函数f1～f3属于单峰目标函数，f4～f6属于多峰目标函数。根据测试函数在不同进化算法中的优化程度，得到每个进化算法对各个测试函数的优化结果，如最优值、平均值、方差等，如表2所示。

从表中可以看出，只有对f3测试函数优化时，差分进化比改进的协同进化在最优值方面略强一些，而从均值和方差来看，改进的协同进化比差分算法在收敛曲线方面比较平稳。改进的协同进化算法在其他测试函数中有明显的改善。

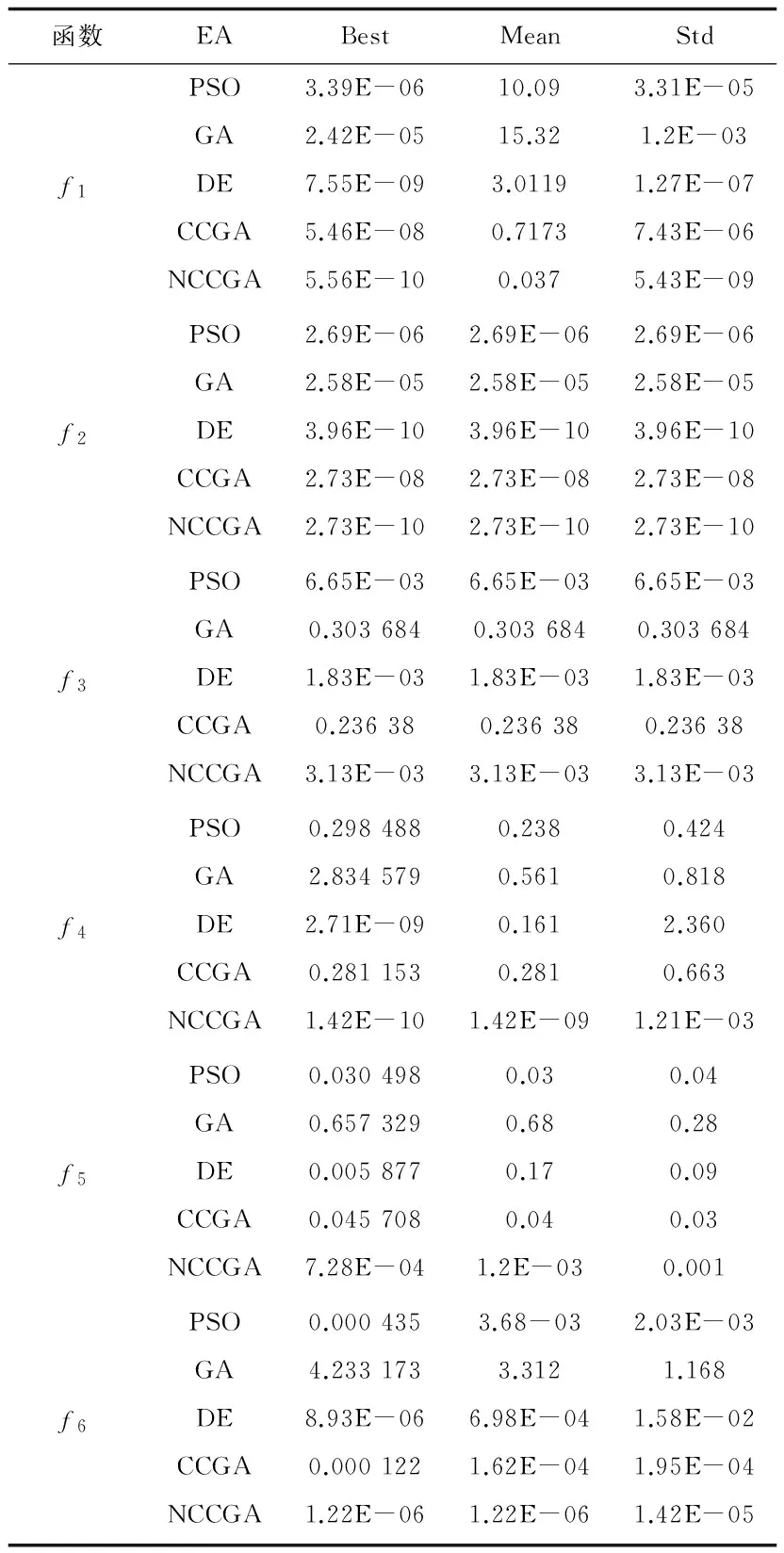
表2 进化算法对测试函数的优化结果

5.2 PID实验仿真

设置迭代计数器m:=0,进化代数50(进化代数计数器m最大值为50)；设定进化终止条件，种群规模n为50，种群个体采用二进制编码，编码长度为20位；设定种群的交叉概率为90%，变异概率为1%；设置最大超调偏差es=-0.1，kp、ki、kd参数范围：kpmin=0，kpmax=50;kimin=0，kimax=50;kdmin=0，kdmax=50。

5.2.1 实验步骤

初始化种群参数kp、ki、kd分别对应种群P1、P2、P3，初始化种群P1(0),P2(0),P3(0)。

所有种群中个体按序组合，例如(P1,j(m),P2,j(m),P3,j(m))(j=1,2,…,50)，将这50个组合代入PID控制器，PID控制系统产生对应的量:tr、δ%、tf、u(t)、e(t)，代入目标函数J，计算相应组合的适应度值，选出最好的一组作为代表组。假设选出的代表个体组为kp=a、ki=b和kd=c，则(a,b,c)作为评估代表组合。判断种群是否达到进化终止条件，若满足条件，则当前评估代表组就作为问题的最优协同解，终止计算。

种群P1(m)中所有个体的适应度值评估，固定ki=b和kd=c,把(P1,j,b,c)(j=1,2,…,50)代入PID控制器系统，产生对应的量：tr、δ%、tf、u(t)、e(t)，代入目标函数J，求出相应的适应度值:

F1,i(i=1,2,…,50)，假设F1,s对应的适应度值最大，F1,s=d，将其中适应度高于当前评估代表组组合中的d替代a，更新评估代表组为(d,b,c)。

各种群中所有个体评估后，根据各种群中每个个体的适应度值，所有种群各自进化，选择合适的进化算法。该进化算法根据种群个体的适应度进行进化操作，如遗传算法的选择、交叉、变异等操作。

EA1、EA2和EA3可以相同也可以不同，进化后得到新一代种群P1,j(m+1)，P2,j(m+1)和P3,j(m+1)，置m：=m+1。

5.2.2 仿真PID参数整定

采用IAE和式(1)的目标函数J，共同验证该方法应用于复杂控制系统的仿真控制效果。

对象传递函数为：

G(s)=

所提算法与其他算法的对比见表3。以J作为目标函数的六种算法响应曲线如图3所示。

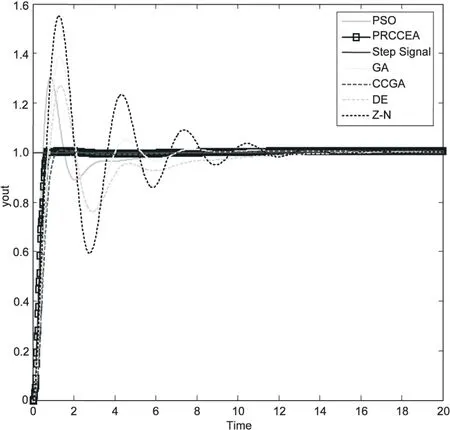
图3 J为目标函数的算法响应曲线图

从表3中可以看出，目标函数在PID整定参数优化方面，改进协同进化算法超调量相对减少了近58.05%，上升时间与整定时间都有了较明显的改善，可见改进算法在PID参数整定方面有了很大提高。

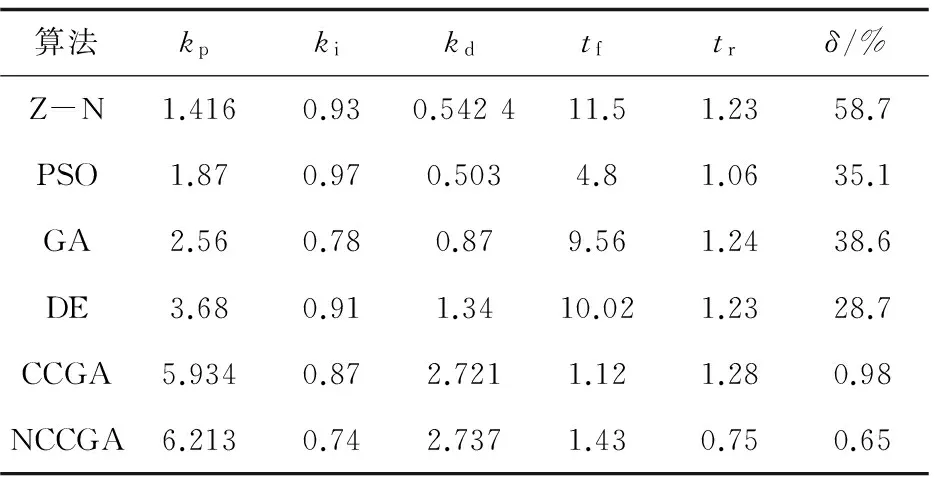
表3 所提算法与其他算法的对比

6 结束语

复杂PID控制器参数整定，选择参数之间协同合作的方式来寻找最优组合。通过控制器参数之间的协同进化，实现控制器参数寻优，其中改进协同进化算法中算法模块选用遗传算法进行验证，算法模块上的进化算法不局限于遗传算法，可以采用其他进化算法进行代替。基于该算法，提出了一种新型的合作协同进化算法，应用于控制系统PID参数整定。合作型协同进化是将控制系统PID三个参数以合作协同的方式进行优化整定。该算法具有精确度较高、收敛速度快、自适应能力较好等特点。但是还有不足之处，处理具有较高的高耦合控制优化问题时，效果不是很好，仍需进一步研究。

[1] Brown R E,Maliotis G N,Gibby J A.PID self-tuning controller for aluminum rolling mill[J].IEEE Transactions on Industry Applications,1993,29(3):578-583.

[2] Saranya M,Pamela A P D.A real time IMC tuned PID controller for DC motor[J].International Journal of Recent Technology & Engineering,2012,1(1):201-206.

[3] Liu G P,Daley S.Optimal-tuning PID controller design in the frequency domain with application to a rotary hydraulic system[J].Control Engineering Practice,1999,7(7):821-830.

[4] Wu C J,Lee T L,Fu Y Y,et al.Auto-tuning fuzzy PID control of a Pendubot system[C]//IEEE international conference on mechatronics.[s.l.]:IEEE,2007:1-6.

[5] Hang C C,Astrom K J,Ho W K.Refinements of the Ziegler-Nichols tuning formula[J].IEE Proceedings-Control Theory and Applications,1991,138(2):111-118.

[6] 欧林林,顾诞英,张卫东.基于幅值裕度和相位裕度的PID参数最优整定方法[J].控制理论与应用,2007,24(5):837-840.

[7] Huang P Y,Chen Y Y.Design of PID controller for precision positioning table using genetic algorithms[C]//IEEE international conference on mechatronics.[s.l.]:IEEE,1997:862-875.

[8] Zhang Y,Hu Y.On PID controllers based on simulated annealing algorithm[C]//Proceedings of control conference.[s.l.]:[s.n.],2008:225-228.

[9] Panda S,Sahu B K,Mohanty P K.Design and performance analysis of PID controller for an automatic voltage regulator system using simplified particle swarm optimization[J].Journal of the Franklin Institute,2012,349(8):2609-2625.

[10] 孟 丽，韩 璞，任燕燕，等．基于多目标粒子群算法的PID控制器设计[J]．计算机仿真，2013，30(7):388-391.

[11] 应明峰,鞠全勇,高 峰.基于粒子群优化的PID控制器设计与应用[J].计算机仿真,2011,28(11):283-287.

[12] Lin C L,Jan H Y,Shieh N C.GA-based multiobjective PID control for a linear brushless DC motor[J].IEEE/ASME Transactions on Mechatronics,2003,8(1):56-65.

[13] Dashti J M,Shojaee G K,Seyedkashi S M H,et al.Novel simulated annealing algorithm in order to optimal adjustment of digital PID controller[C]//International conference on control automation robotics & vision.[s.l.]:[s.n.],2010:1766-1771.

[14] Nangru D,Bairwa D K,Singh K,et al.Modified PSO based PID controller for stable processes[C]//International conference on control,automation,robotics and embedded systems.[s.l.]:IEEE,2013:1-5.

[15] Potter M A, Dejong K A. A cooperative coevolutionary approach to function optimization[C]//Proceedings of the third conference on parallel problem solving from nature.Berlin:Springer,1994:249-257.

[16] Potter M A,Jong K A D.Cooperative coevolution:an architecture for evolving coadated subcomponents[J].Evolutionary Computation,2000,8(1):1-29.

[17] 余胜威,曹中清.基于人群搜索算法的PID控制器参数优化[J].计算机仿真,2014,31(9):347-350.

PID Parameters Optimization with Improved Cooperative Coevolution Algorithm

MEI Ling，LUO Jie

(College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

Aiming at the parameter tuning problem of PID control in complex system,a parameter optimization method of PID controller based on improved collaborative coevolution has been proposed to realize the optimal combination of three parameters of PID in the co-evolutionary way under the given performance index.Based on the PID controller model,a more optimized objective function of PID parameters has been designed.Combined with the cooperative co-evolutionary algorithm for optimization of the parameters,the group sorting strategy before PID parameters co-evolution is put forward based on the cooperative evolution algorithm.The optimal group is selected as the next generation of representative combination of co-evolution in accordance with results of group sorting strategy to evaluate the merits of packet sorting.The simulation results show that the proposed algorithm has better optimization effect than the traditional one,and has fast convergence speed,strong adaptability and high precision,with a better application prospects.

PID parameter tuning;co-evolution;sorting strategy;optimization objective function

2016-09-04

2016-12-08 网络出版时间：2017-06-05

江苏省自然科学基金项目(BK2011758)

梅 领(1992-)，男，硕士，研究方向为智能控制；罗 杰，博士，教授，研究方向为分布式智能控制、群体智能。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170605.1510.076.html

TP301.6

A

1673-629X(2017)08-0037-06

10.3969/j.issn.1673-629X.2017.08.008