善用旧瓶尝新酒——例谈新定义类题目的解题策略

北京 杜巧卫

(作者单位：北京师范大学出版集团)

善用旧瓶尝新酒
——例谈新定义类题目的解题策略

在近年各地的高考题和模拟考试中，经常能见到一类“新定义”问题.这些题目一般在题设条件中给出课本上没有的定义、概念或性质，要求考生解决与之相关的问题.很多同学对这一类问题感到困难，畏惧于题目给出的五花八门的新定义，甚至对一些有一定难度的题目感到无所适从.

其实，只要仔细分析这些题目就可以看出，这些所谓的“新定义”其实就是对传统题目中的题设条件或设问换了一种说法，本质上都属于“旧瓶装新酒”.只要我们掌握好、用好这个“装酒的旧瓶”(即基本的数学概念和基础的数学思想、解题方法)，就能品尝瓶中的“新酒”(给出的新定义新概念)，不论是醇厚的佳酿还是浓郁的烈酒，都能从容应对.下面我们就以2016年的几道高考真题为例，谈谈解决这类新定义问题的策略和方法.

【例1】(2016·山东理·10)若函数y=f(x)的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称y=f(x)具有T性质.下列函数中具有T性质的是

( )

A.y=sinxB.y=lnx

C.y=exD.y=x3

【试题分析】题意中的T性质，是指函数图象上存在两个点，这两点处的切线互相垂直，实质上是函数图象上存在两点的导数值乘积等于-1的情况.依次验证选项中的函数的导数是否满足这个要求即可.

【解】当y=sinx，可知y′=cosx, 所以cos0·cosπ=-1，所以函数y=sinx的图象上存在两个点，使在这两个点处的切线互相垂直，满足T性质.而其他函数y=lnx，y=ex，y=x3的导数值均为非负数，所以均不具有T性质.故选A.

【评注】本题给出的“新定义”，其实只是传统题目条件及设问的另一种表述方式，本质上还是在考查函数的求导和导数的几何意义，所以理解给出的新定义或新性质的含义，进行适当的转化是解题的关键.

①若点A的“伴随点”是点A′，则点A′的“伴随点”是点A;

②单位圆的“伴随曲线”是它自身；

③若曲线C关于x轴对称，则其“伴随曲线”C′关于y轴对称；

④一条直线的“伴随曲线”是一条直线.

其中的真命题是 (写出所有真命题的序号).

【试题分析】本题题意中给出的“伴随点”的概念，实质上是给出了一种坐标变换，但应注意这种变换不一定是可逆的.判断给出的命题是否为真命题时，既可以根据伴随点的定义直接验算，也可以举出反例判断，后者的方法往往更简单.

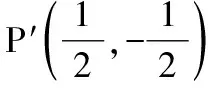
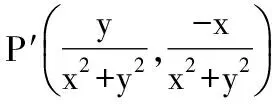
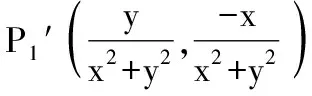
综上，本题应填②③.

以上两道“新定义”类问题比较简单，甚至可以说这两道道题目不仅“盛酒的酒瓶”(即解题需要的技能和方法)是旧的，连 “瓶中的美酒”(即题设中给出的新定义)也是旧的，无非是在酒瓶上换了一个标签而已！这类题目一般比较简单，只要同学们能够把握给出的“新定义”的本质，并将其转换为我们熟悉的概念和性质，就能顺利求解.

高考中还有一类“新定义”问题，它们一般出现在解答题中，有的甚至是在压轴题中.这些题目给出的“新定义”往往无法直接转化成我们熟悉的概念或性质，而要求同学们在认真研究给出的新定义同时，还必须深入挖掘蕴含在定义中的性质，并熟练运用基本的数学思想和方法才能顺利解决.下面我们通过对2016年北京高考数学理科卷的压轴题的分析和解答来加以说明.

【例3】(2016·北京理·20)设数列A：a1,a2，…，aN(N≥2).如果对小于n(2≤n≤N)的每个正整数k都有ak

(1)对数列A：-2，2，-1，1，3，写出G(A)的所有元素；

(2)证明：若数列A中存在an使得an>a1，则有G(A)≠∅；

(3)证明：若数列A满足an-an-1≤1(n=2,3，…，N)，则G(A)的元素个数不小于aN-a1.

【试题分析(1)】本题给出的新定义“G时刻”不能简单地转化为我们学过的数学概念或性质，需要认真分析它的定义，并挖掘其蕴含的性质.为此，我们可以画出一个数列图象的草图帮助我们理解题意并分析，如下图.图中加下划线的序号，即为此数列的“G时刻”，我们把它们对应的项用虚线连成了一条曲线.

对照题意给出的“G时刻”的定义，即“如果对小于n(2≤n≤N)的每个正整数k都有ak

【解】(1)数列A：-2，2，-1，1，3中，第2项大于第1项，第5项大于之前的4项，故数列A的G时刻为2和5，所以G(A)的元素为2和5.

【试题分析(2)】题意要求证明当数列A中存在an使得an>a1时，则数列A存在“G时刻”，参考上面给出的数列图象，可以看出，如果数列A中存在大于a1的项，那么第一个大于a1的项对应的项数，即是此数列的G时刻，根据这个思路，便不难证明第(2)问.注意解题时要使用严谨的数学语言.

【证明】(2)因为数列A中存在an使得an>a1，

所以{i∈N*|2≤i≤N,ai>a1}≠∅.

设m=min{i∈N*|2≤i≤N,ai>a1}，

则m≥2，且有当k∈N*且k

所以根据定义可知m∈G(A)，所以G(A)≠∅.

【试题分析(3)】本题第三问有一些难度，很多同学做到这一问时会感到没有头绪.这就需要我们在初步掌握了G时刻的定义后，还要继续挖掘蕴含在这个概念中的数学性质，并结合题设条件和要求证明的结论加以分析.

不妨设G(A)的元素个数为p，则题目条件为“数列A满足an-an-1≤1”，要证明的结论为“p≥aN-a1”.由“aN-a1”和“an-an-1”的式子特点，我们可以联想到要用到“累加法”.再由p为G(A)的元素个数，这就提示我们进一步研究数列A的G时刻对应的项的性质.

通过图象可以看出，G时刻对应的数列中的项是单调递增的，这应该是G时刻的基本性质.

不妨设G(A)={n1,n2,n3,…,np}，且n1

进一步观察图象，研究G时刻的性质，我们可以得出，若在相邻的G时刻ni,ni+1对应的项ani,ani+1之间还有其他的项，则这些项必不大于ani.再结合数列A满足an-an-1≤1的条件，不难得出ani+1≤an(i+1)-1+1≤ani+1，即ani+1-ani≤1；若ani,ani+1之间没有其他的项，即ani,ani+1是数列A中相邻的两项，由题设条件也可得ani+1-ani≤1，而ani+1-ani≤1正是我们要使用累加法所需要的关系式.将上面的思路整理一下，用严谨的数学语言表述出来，即可得到第(3)问的证明.

【证明】(3)不妨设G(A)的元素个数为p，则p≥0.

若aN≤a1，则aN-a1≤0≤p，命题成立.以下设aN>a1，由第(2)问可知G(A)≠∅.

设G(A)={n1,n2,n3,…,np}，且1

由G时刻的定义可知:a1

设2≤i≤p,且ni∈G(A)={n1,n2,n3,…,np}，若ni-ni-1=1，则有ani-an(i-1)≤1；

若ni-ni-1>1，设Gi={k∈N*|ni-1ani-1}，若Gi≠∅，令mi=minGi，所以mi∈G(A)，矛盾.所以若ni-1

所以ani≤1+ani-1≤1+an(i-1)，即ani-an(i-1)≤1.

(注意“an(i-1)”表示第(i-1)个G时刻对应的项；而“ani-1”表示第i个G时刻对应的项的前一个项)

所以an1-a1≤1,

an2-an1≤1,

an3-an2≤1,

……

anp-anp-1≤1，

即G(A)的元素个数不小于aN-a1.证毕.

【评述】本题给出的新定义比较抽象，需要我们借助实例、图象来深入理解，但本题考查的仍是高中数学基本的概念和方法.第(3)问的证明有一定的难度，不仅需要考生通过对题设条件和待证式的结构特征的观察联想到要用到“累加法”，还要求考生能挖掘出“G时刻”的相关性质，并结合题设条件由定性的性质得出定量的结果.

(作者单位：北京师范大学出版集团)