构造模型探究空间动点轨迹

江西 廖达凡

(作者单位：江西省大余中学)

构造模型探究空间动点轨迹

在近几年的高考试题中，以空间图形为载体的轨迹问题以它独特的知识性、趣味性、新颖性和综合性已悄然成为试题中一道亮丽的风景线.此类问题将解析几何知识和立体几何知识结合在一起，在知识网络交汇处设计命题，灵活、巧妙地考查学生的思维能力和空间想象能力.针对高考复习中有不少同学对这类问题难以把握,笔者举例探讨如何巧妙构造图形来解决动点轨迹，以飨读者.

一、构造正方体探究动点轨迹问题

【例1】(2010·重庆理·10)到两互相垂直的异面直线的距离相等的点，在过其中一条直线且平行于另一条直线的平面内的轨迹是 .

A.直线

B.椭圆

C.抛物线

D.双曲线

【解析】根据题意，可构造正方体为模型来研究，设正方体的棱长为1.

如图，图中AB与A1D1是满足条件的两条异面直线，平面ABCD就是过异面直线中的一条AB与另一条直线A1D1平行的平面，在平面ABCD内以A点为原点，AB与AD所在直线分别为x轴、y轴建立平面直角坐标系.设点P(x，y)是平面ABCD内满足条件的动点.过点P分别作PR⊥AB，PQ⊥A1D1，作PS⊥AD于S，连接QS，由线面关系不难知QS⊥PS.

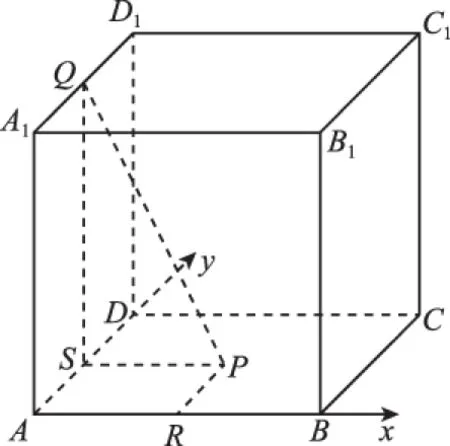
【评注】此题为立体几何背景下考查学生平面解析几何的知识，图形比较抽象，若能构造出一个正方体，就可直观地表现出各个量之间的关系，再把各个量转换到平面上就可研究.

二、构造圆柱探究动点轨迹问题

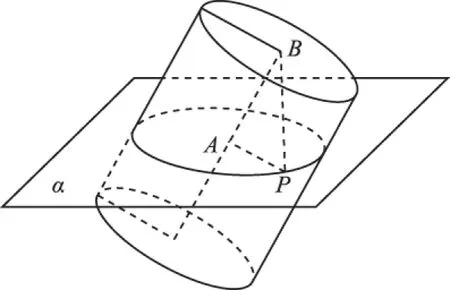
【例2】(2008·浙江理·10)如图，AB是平面α的斜线段，A为斜足，若点P在平面α内运动，使得△ABP的面积为定值，则动点P的轨迹是 .

A.圆

B.椭圆

C.一条直线

D.两条平行直线

【解析】因为△ABP的面积为定值，且AB为定长，所以点P到直线AB的距离就为定值.空间中，动点P到直线AB的距离为定值的轨迹为一个以AB为轴的圆柱，且点P在平面α内运动.故可以构造圆柱用一个平面斜截圆柱侧面，所截得的截线就是椭圆，故选B.

【评注】本题将问题转化后，构造出圆柱就可很好地解决问题了，能力要求比较高.

三、构造平面探究动点轨迹问题

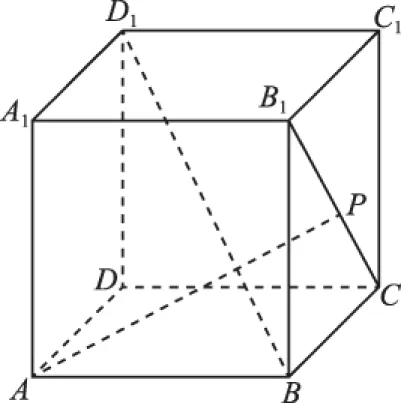
【例3】如图，在正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总保持AP⊥BD1，则动点P的轨迹是 .

A.线段B1C

B.线段BC1

C.BB1中点与CC1中点连成的线段

D.BC中点与B1C1中点连成的线段

【解析】联想正方体的体对角线与面对角线的关系.连接AC、CB1、AB1，易证BD1⊥平面AB1C，所以点P的轨迹为线段B1C.

(作者单位：江西省大余中学)