二项式中的系数问题

山东 杨宗柱

(作者单位：山东省泰安英雄山中学)

二项式中的系数问题

一、求展开式中项的系数

【例1】(2016·北京)在(1-2x)6的展开式中，x2的系数为 .(用数字作答)

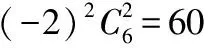
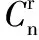
二、求展开式中与系数相关的参数

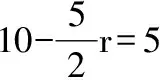
【点评】已知二项式展开式中某一项的系数，求相关参数的值，是二项式定理的逆向应用.解这类问题主要是利用通项公式，建立关于参数的方程，由待定系数法求解.

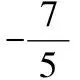
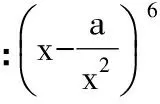
三、求两个二项式积的展开式中项的系数

【例3】(2014·浙江理·5)在(1+x)6(1+y)4的展开式中，记xmyn项的系数为f(m,n)，则f(3,0)+f(2,1)+f(1,2)+f(0,3)=( )

A.45 B.60 C.120 D.210

【点评】求两个二项式积的展开式中某一项的系数，可分别展开两个二项式，由多项式乘法求得所求项的系数.

【变式3】 (1+2x)3(1-x)4展开式中x2的系数为 .

提示：因为(1+2x)3(1-x)4展开式的通项为

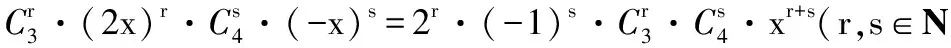
又由题意知r+s=2，

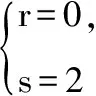
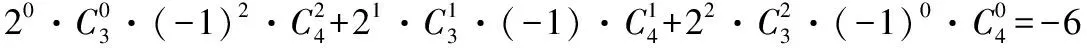
四、赋值法求展开式各项系数的和

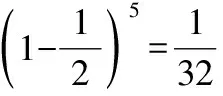
【点评】求二项式所有项的系数和，可采用“特殊值取代法”，通常令字母变量的值为1.

( )

A.-60 B.60

C.-30 D.30

五、求系数最大的“项”

(Ⅰ)若展开式中第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大项的系数；

(Ⅱ)若展开式前三项的二项式系数和等于79，求展开式中系数最大的项.

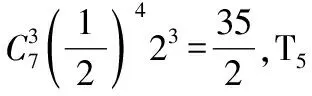
当n=14时，展开式中二项式系数最大的项是T8.

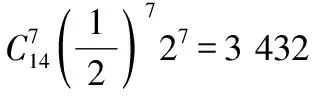
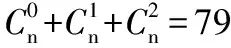
所以n=12或n=-13(舍去).

设Tk+1项的系数最大，

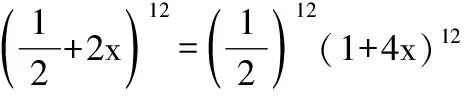
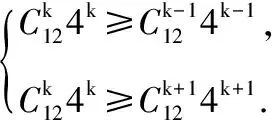
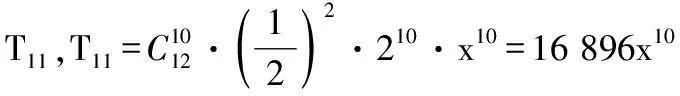
【点评】二项式系数、系数是两个不同的概念，二项式系数最大的项一定是展开式中的中间项(或中间两项)；而系数最大的项通过解不等式组的方法解决，且一定要考虑到系数前的符号.

六、综合应用

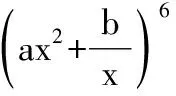
【点评】本题与基本不等式的应用结合，考查了二项式展开式的项的系数的逆向应用，体现了知识间的交汇.

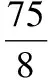
(Ⅰ)求a的值；

(Ⅱ)若(xcosθ+1)5的展开式中x2的系数与(x+a)4的展开式中x3的系数相等，试求cos2θ的值.

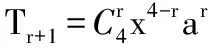
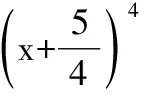
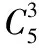
故cos2θ=2cos2θ-1=0.

(作者单位：山东省泰安英雄山中学)