数列“函数”角色的精彩演绎

广东 林锡龙

(作者单位：广东省惠来一中)

数列“函数”角色的精彩演绎

数列是自变量为正整数的特殊函数，其项数n对应函数的自变量x，其通项公式an对应函数的解析式f(x).利用函数的单调性可以研究数列的单调性，进而可研究数列的最大项、最小项问题.可是在实际应用中，如果把研究数列的单调性的方法完全等同于研究函数的单调性的方法的话，往往会出现这样或那样的问题.本文通过引入两者异同并结合例题分析，探究如何做到将数列的“函数”角色演绎精彩.

一、两者异同

1.同：数列{an}与函数f(x)有着一样的渊源，都属于映射

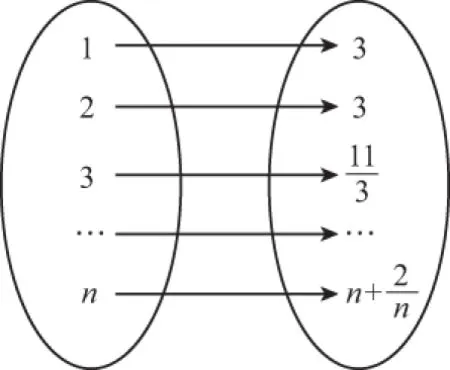
图1

图2

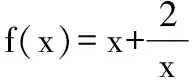
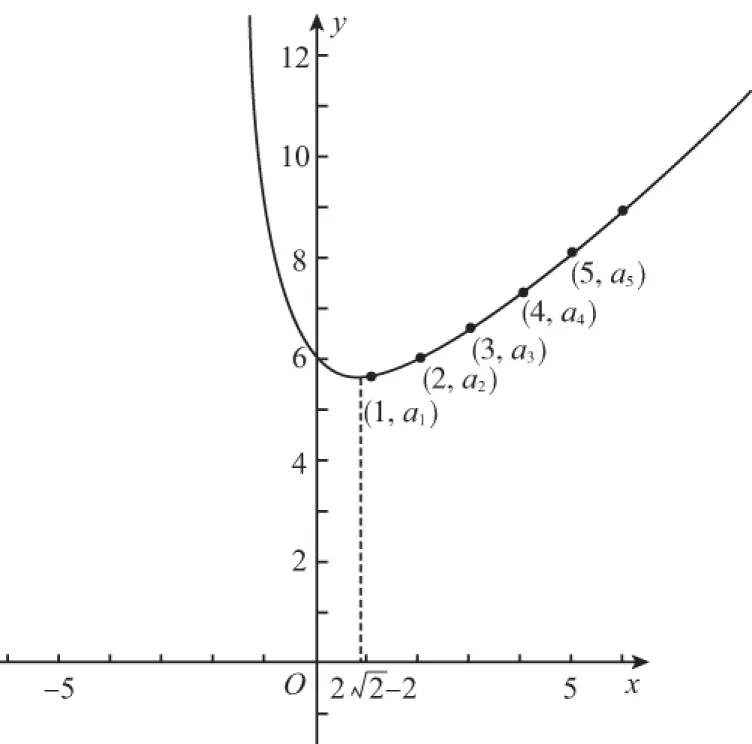
2.异：(n,an)只是其同源函数f(x)图象上一系列孤立的点

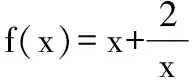
由于数列的单调性与其同源函数的单调性不尽相同，所以在解决最值问题时，学生往往忽视了n∈N*而发生错误.

二、数列的最值问题转化为同源函数的最值问题

【例1】(2016·新课标Ⅰ)设等比数列{an}满足a1+a3=10，a2+a4=5，则a1a2…an的最大值为________.

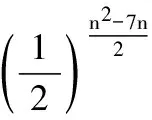
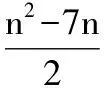
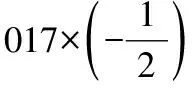
又因为29=512，210=1 024，211=2 048，

……

……

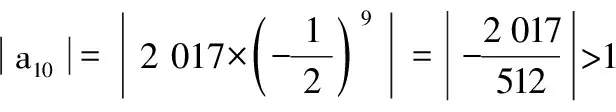
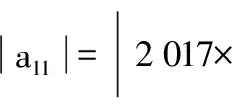
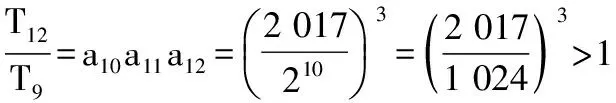
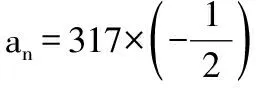
【例3】(2016·宁波模拟)等差数列{an}的前n项和为Sn，若数列{Sn}有唯一的最大项S3，Hn=S1+2S2+3S3+…+nSn，则( )

A.S5·S6<0

B.H5·H6<0

C.数列{an}、{Sn}都是单调递减数列

D.H6可能是数列{Hn}的最大项

“社会越来越充满喧闹，连本来是宁静的大学校园，如今与喧闹的市井大街也没有多大的区别。”作家张炜为此写了一篇《寻获安静》的文章。网络上有个热词，叫作“我想静静”，曾入选2015年度十大网络用语，尽管它的“热”，是由于其中有被（故意）曲解为“我想念静静”的意思在，但它的原意毕竟是“让我静一静”，反映了许多人“寻求安静”的心声。

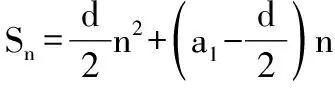
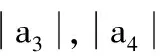
对于选项B，H5·H6=(55a1+85d)(91a1+175d)=[55(a1+2d)-25d]·[91(a1+2d)-7d]，因为a1+2d>0,d<0，所以H5·H6>0，所以B错；

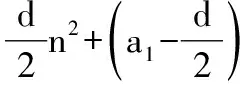
对于选项D，因为5S5=15a3>0，6S6=18(a3+a4)，7S7=49a4<0，8S8=32(a4+a5)<0，所以当6S6=12(a3+a4)>0时，H6为{Hn}的最大项；当6S6=18(a3+a4)<0时，H5为{Hn}的最大项.所以D正确.

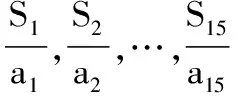
【解析】因为S15>0,S16<0，所以S15=15a8>0,S16=8(a8+a9)<0，所以a8>0，a9<0，由等差数列各项的性质(各项递减)可知，a1,a2,…,a8>0，a9,a10,…，a15<0.

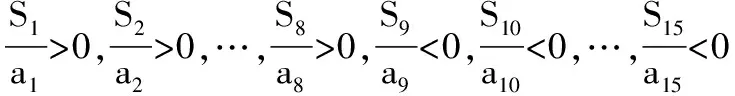
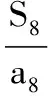
三、数列的恒成立问题化归为数列的最值问题

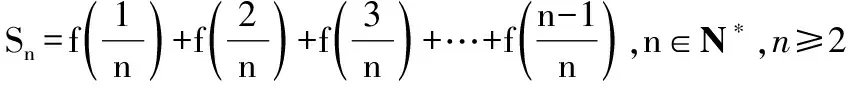
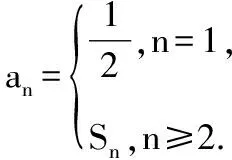
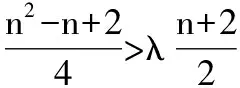
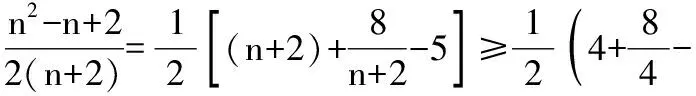
当n=1时，T1>λ(S2+1)，

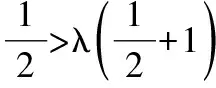
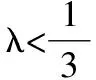
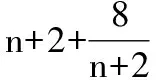
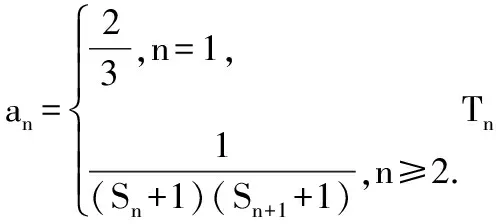
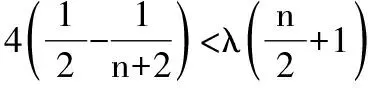
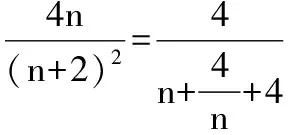
(作者单位：广东省惠来一中)