运用“点圆”法求圆的方程
山西 李有贵
运用“点圆”法求圆的方程

在平面解析几何中,求解有关方程的问题时,往往要建立方程组,借助于解方程的方法进行求解,但由于未知数较多,从而容易造成“入手容易”“答对困难”的现象.其主要原因是未知数多,运算量大,这样不仅影响了解题速度,也极容易出错.因而,尽量减少运算量是快速、准确解答此类问题的关键.为此,本文将介绍运用“点圆”的思想巧求方程的方法,供同学们借鉴与参考,从而启迪思维,提高解题能力.
【例1】有一圆与直线4x-3y+6=0相切于点A(3,6),且经过点B(5,2),求此圆的方程.
【解】将点A(3,6)表示成“点圆”形式:(x-3)2+(y-6)2=0,设所求圆的方程为(x-3)2+(y-6)2+λ(4x-3y+6)=0,将点B(5,2)代入上述圆方程得,λ=-1.
所以满足条件的圆方程为(x-3)2+(y-6)2-(4x-3y+6)=0
即x2+y2-10x-9y+39=0为所求的圆方程.
【评注】本例大家需要做好两个准备:
其一:所谓“点圆”,就是将平面上某一点看成是以此点为圆心,半径为0的圆,即约定点(a,b)的方程为(x-a)2+(y-b)2=0;
其二:过直线Ax+By+C=0与圆(x-a)2+(y-b)2-r2=0的公共点的圆系方程为
(x-a)2+(y-b)2-r2+λ(Ax+By+C)=0,
过两圆x2+y2+D1x+E1y+F1=0与x2+y2+D2x+E2y+F2=0的公共点的圆系方程为x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0.
【例2】求经过点M(4,-1),且与圆C:x2+y2+2x-6y+5=0相切于点N(1,2)的圆方程.
【解】将点N(1,2)表示成“点圆”形式,
即(x-1)2+(y-2)2=0,
设所求的圆方程为
(x-1)2+(y-2)2+λ(x2+y2+2x-6y+5)=0,
将点M(4,-1)代入上式得
18+36λ=0,

所以满足条件的圆方程为

即(x-3)2+(y-1)2=5为所求的圆方程.
【评注】切点看成点圆,这时所求圆就是过已知圆与点圆的公共点的圆,因而可以过两圆公共点的圆系方程求解.设出圆系方程,代入点M的坐标就可求出圆的方程.常规解法,求出线段MN的垂直平分线l1的方程,以及直线CN的方程,两直线l1,CN的交点即为圆心A,再求出AN的长度,得到圆的方程.
【例3】求与直线l1:4x-3y+25=0相切于点A(-4,3),且半径为5的圆方程.
【解】将切点(-4,3)表示成“点圆”形式,
即(x+4)2+(y-3)2=0,
设所求的圆方程为
(x+4)2+(y-3)2+λ(4x-3y+25)=0,
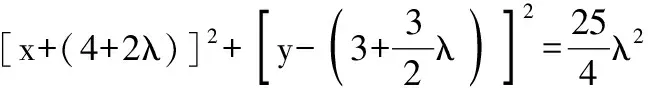
因为此圆半径为5,
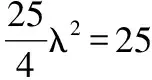
即λ=±2
故所求的圆方程为(x+8)2+(y-6)2=25或x2+y2=25.
【评注】切点看成点圆,这时所求圆就是过直线与点圆的公共点的圆,因而可以用过直线与圆公共点的圆系方程求解.设出圆系方程,将方程变成圆的标准形式,利用半径为5,求出λ的值,因而得到圆的方程.常规解法,求出以A为圆心5为半径的圆的方程与过A(-4,3)垂直于直线l1的直线l2的方程的交点,得到两个圆心坐标,写出圆的方程.
【例4】求圆心在直线l1:2x+y=0,且与直线l2:x+y=1相切于点A(2,-1)的圆的方程.
【解】将点(2,-1)表示成“点圆”形式,
即(x-2)2+(y+1)2=0.
设所求的圆方程为(x-2)2+(y+1)2+λ(x+y-1)=0,
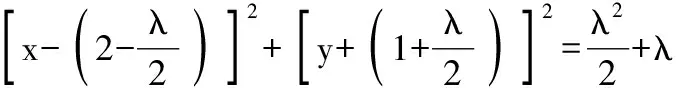
因圆心在直线2x+y=0上,

即λ=2,
所以所求圆的方程为
(x-1)2+(y+2)2=4.
【评注】切点看成点圆,这时所求圆就是过直线与点圆的公共点的圆,因而可以用过直线与圆公共点的圆系方程求解.设出圆系方程,找到圆心坐标,代入圆心所在直线方程,求出λ的值,因而得到圆的方程.常规解法,先求出点A(2,-1)与直线l2垂直的直线l3的方程,再求出两直线l1,l3的交点,即为圆心M.最后求出MA的长度,得到圆的方程.

山西省临县第一中学)

