均值不等式应用例析

福建省福安市第二中学 罗开华

均值不等式应用例析

福建省福安市第二中学 罗开华

利用均值不等式及推广求解最值问题、不等式证明、实际问题。均值不等式教学对优化学生知识结构、提升应用能力具有重要意义。

均值不等式；应用与推广

均值不等式作为高中课程的重要知识，要掌握两个正数的算术平均数不小于它们的几何平均数并会简单的应用。应用均值不等式求最值问题、不等式证明、解决实际问题具有重要作用。同时，均值不等式的教学有助于培养学生的数学创新意识，对探索创造、发挥潜能、开发智力具有重要意义。

一、均值不等式及其推广

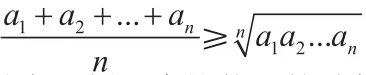
二、均值不等式的应用

1.均值不等式在最值问题中的应用

2.均值不等式在证明不等式中的应用

运用均值不等式进行不等式的证明，可使很多问题更为简便转化和解决,使不等式的证明更具有活力和灵活性。

（还可以用三角代换、常值代换、消元法等方法处理）

3.均值不等式在实际问题中的应用

例5 某工厂购买某种设备时费用为10万元，每年的设备运营费为9千元，设备的维修费为第一年2千元，第二年4千元，…依每年2千元递增,问该设备使用多少年报废最合算（使用年平均费用最少）？

解：设该设备使用n年报废，则每年平均费用为f(n)万元，依题知：每年设备的使用费与维修费之和构成首项为1.1，公差为0.2的等差数列，前n项和为0.1n²+n万元，依题有：答：该设备使用10年报废最合算。

三、反思与感悟

均值不等式作为一个重要的不等式，在求函数最值、不等式证明及实际问题求解中发挥重要作用，其应用十分广泛。但要注意应用条件：“一正二定三等”，不满足条件时要创造条件，利用配凑法、函数单调性、拆项添项等方法处理。教师要重视均值不等式的教学，锻炼学生的推理能力、想象力和创造力，促进学生思维能力的发展。