初中数学教学中学生创新能力的培养
江苏省海门市长春初级中学 杨顾卫
初中数学教学中学生创新能力的培养
江苏省海门市长春初级中学 杨顾卫
在初中数学课程指导中,教师除了要让学生掌握基础知识点的原理及指导概念的认识外,还要注重对学生创新能力的培养,激发学生的创造力对学生综合素质水平的提高以及学习能力的增强来说有重要意义。本文就以初中数学教学为例,就有关学生创新能力的培养策略进行相关探讨。
初中数学教学;创新能力培养;一题多解
随着新课程标准改革内容的逐渐深入,对实际课堂教学也提出了更多要求,在培养学生创新能力的教学研究中,通过在日常教学指导中引入一题多解以及温故知新的教学概念,由此可带给学生更加科学高效的教学体验。下面就具体地针对学生创新能力培养的教学方式进行详细说明。
一、力求一题多解,渗透创新思想
初中数学学习在数量方面的教学指导中,可以先引导学生将复杂的数量关系结合图形,利用数形结合将两者所要考查的内容进行融合,再从两者不同的解题方式上思考,从而认识到更多不同种类的解题技巧。例如题目:如图1,OP是∠MON的平分线,请你利用这个图形画一对以OP所在直线为对称轴的全等三角形。请你参考这个作全等三角形的方法,思考以下问题:
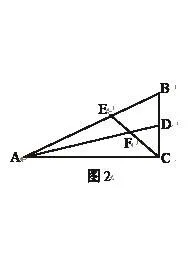
(1)如图2,在△ABC中∠ACB是直角,∠B=60º,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F,求FE与FD之间的数量关系;
(2)如图3,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不改变,请问,在(1)中所得到的结论是否仍然成立?如果成立,请证明:如果不成立,请说明理由。


由题可知,在思考该类几何证明题时,可先从添加辅助线的方式开始,通过添加辅助线进而为解题提供更加直接明了的思路。比如在第一问中,我们可以利用作全等三角形的方法:过OP上一点C作OM和ON的垂线,交OM于A,交ON于B,则有△OAC≌△OBC(角角边)。
(1)连接BF,因为三角形三条角平分线交于一点,
所以BF为∠B的角平分线,同时过F点做BA和BC的垂线,交BA于M,交BC于N,
所以△BMF≌△BNF,于是MF=NF。
在Rt△FDN与Rt△FEM中,
所以△FDN≌△FEM,所以EF=DF。
(2)结论依然成立,
连接BF,由(1)知BF为∠B的角平分线,同时过F点做BA和BC的垂线,交BA于M,交BC于N,
所以△BMF≌△BNF,于是MF=NF。
在△FDN与△FEM中,
所以△FDN≌△FEM。所以EF=DF。
利用添加的辅助线来达到解题目的,不同的辅助线添加也会有不同的证明过程,这里教师可以引导学生向着多种不同的辅助线添加方式进行尝试,进而达到一题多解的教学目的。
二、倡导师生互动,挖掘创新因子


图4
初看题目会觉得由角度之间以及线与线位置之间的关系证明很难扯上关系,但是师生进行互动探讨,可以将题中隐藏的各个条件结合起来,这里就可将每个角对应的大小与位置等几项重要信息联系在一起,进而理清思路,把几何证明变得清晰明白。具体解题思路如下:

由题我们可以分析得出,题中有关角的已知条件较多,经过师生互动讨论我们知道可对角进一步进行转化,将直线之间的关系反映成对应的角,以此来丰富已知内容。基于分析课程,在对几何章节进行学习时,不能让学生死学,要灵活运用和转变已知条件,进而达到解题的目的。
三、鼓励发散聚焦,探讨创新方法

总之,培养学生的创新能力,要注重从学生解题思维发散上开始着手,在日常习题训练中力求一题多解,从而强化学生对创新思维观念的认识。当下创新教学中一改传统的只重注学生会解题、能得分的教学观念,而从强调创新能力培养方面上展开,十分符合新时代对人才培养的标准要求。
[1]朱汝胜.初中数学课堂教学中学生创新能力的培养[J].数学大世界(上旬),2016(10).
[2]杨叶海.如何加强数学教学中学生创造思维的培养[J].读与写(教育教学刊),2008(04).
[3]任常梅,苏翠英.浅谈数学教学中创新意识的培养[J].齐鲁师范学院学报,2000(06).

