一道课本习题的解法探究
厦门大学附属实验中学(363123) 袁海军
一道课本习题的解法探究
厦门大学附属实验中学(363123) 袁海军
引例(人教A版普通高中课程标准实验教科书必修5教材69页第6题)已知数列{an}中a1=5,a2=2,an=2an−1+3an−2(n≥3),对于这个数列的通项公式作以研究,能否写出它的通项公式?
说明此题作为课本作业,学生完成的情况很不理想,有的学生仅写出前若干项,想通过观察、归纳写出通项,结果解题思路陷入了更加迷茫、繁杂的困境,无法形成有效的解题突破,大多数学生缺乏对此题解法的理解和相应的构造策略,从而引起我对此类题型解法的进一步探究和归纳.
解法一教师用书提供的参考答案:由已知an=2an−1+3an−2(n≥3)可得:an+an−1=3(an−1+an−2),又an−3an−1=−(an−1−3an−2),所以
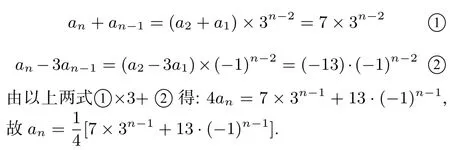
若按照教科书提供的参考答案,看起来简单流畅,只是很自然地先构造两个等比数列,然后再解两个方程消元即可.其实细细思考,要想构造出两个方程式,对于学生是很困难的,这种构造来的太突然,技巧性太强.那么我们要如何探索这种题型的常规解法呢?在数列中常涉及构造法的题型有哪些呢?
类型一形如an+1=Aan+D(A≠0,1,D≠0)的数列,求an.
思路方法an+1=Aan+D,可变形为


点评这类题是高考的热点和重点,一定要牢牢掌握它的变形本质;只是进行一次变式把数列化归为等比数列.
类型二形如an+1=Aan+C·n(A≠0,1,C≠0)的数列,求an.
思路方法an+1=Aan+Cn,可变形为

解因为a1=−4,an+1=5an+16n,可变形为:an+1+4(n+1)+1=5(an+4n+1),令bn=an+4n+1,因为a1=−4,所以b1=1.则构造数列{bn}是公比为5的等比数列,所以bn=an+4n+1=1×5n−1=5n−1,即an=5n−1−4n−1.
注意:当A=1时.就是典型的叠加法和迭代法,这类题仍是高考的热点和重点.
点评一般地,对于形如an+1=an+f(n)类的通项公式,只要f(1)+f(2)+···+f(n)能进行求和,则宜采用此方法求解.
类型三形如an+1=Aan+Btn(A≠0,B≠0,t≠1)的数列
思路方法an+1=Aan+Btn可变形为:

例3. 已知数列{an}满足:a1=16,an+1=4an−3·2n+1(n∈N∗),求an.

从而就可以构造一个新的等比数列{an−3·2n},其首项a1−3·21=16−6=10,公比q=4,所以有an−3·2n=10×4n−1=5·22n−1,即an=5·22n−1+3·2n.

点评an+1=f(an)且为一次分式型或构造出倒数成等差数列或构造出倒数加常数成等比数列,发散之后,两种构造思想相互联系,相互渗透,最后融合到一起.
类型六an+2=Aan+1+Ban,且已知a1,a2的值,(A≠0,B≠0),求an.
思路方法an+2=Aan+1+Ban可变形为:展开得:


由待定系数法得:xy=B,y−x=A,解出x,y,从而构造等比数列:an+2+x·an+1=y(an+1+x·an),再回到类型一或类型三.
又回到引例:已知数列{an}中a1=5,a2=2,an=2an−1+3an−2(n≥3),对于这个数列的通项公式作以研究,能否写出它的通项公式?
解法二因为an+2+x·an+1=y(an+1+x·an),即an+2=(y−x)an+1+x·yan=2an+1+3an,即xy=3,y−x=2.可得y=3,x=1或y=−1,x=−3.分别代入可得:an+an−1=3(an−1+an−2),又a1+a2=7,数列{an+an+1}形成首项为7,公比为3的等比数列,则
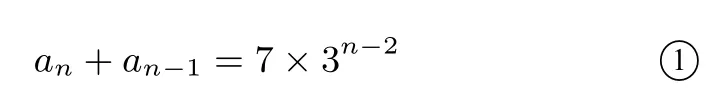
又an−3an−1=−(an−1−3an−2)a2−3a1=−13,数列{an−3an−1}形成了一个首项为−13,公比为−1的等比数列,则

由以上两式①×3+②得:4an=7×3n−1+13·(−1)n−1,故
解法三因为an+2+x·an+1=y(an+1+x·an),即

即xy=3,y−x=2.可得y=3,x=1或y=−1,x=−3.分别代入可得:an+an−1=3(an−1+an−2),又a1+a2=7,数列{an+an+1}形成首项为7,公比为3的等比数列,则an+an−1=7×3n−2.又由

以上解法二、三相比解法一更为清晰,思路更有条理性,层层深入,学生也容易理解、掌握.
点评已知数列f(an+2,an+1,an)=0的关系,可先把复合数列通过待定系数法转化为等差数列或等比数列,再用其它基本方法求得an.如本题是两次构造等比数列,最终用加减消元的方法确定出数列的通项公式.此法较为简洁明了.
特别注意已知数列f(an+2,an+1,an)=0的关系,但如果复合数列通过转化难以构成等差、等比数列,有时可考虑构成循环关系而求出an.
例6. 在数列{an}中,a1=1,a2=5,an+2=an+1−an,求a2012.
解由条件an+3=an+2−an+1=(an+1−an)−an+1=−an即an+3=−an,所以an+6=−an+3=an即数列周期为6,每间隔6项循环一次.2012=6×335+2,所以a2012=a2=5.
类型七多种形式构成的综合型,求an.
例7. 已知数列{an}的首项a1=1,前n项和为Sn,且Sn+1=4an+2(n∈N∗),求an.
解当n≥2时,Sn+1=4an+2,Sn=4an−1+2.两式相减,得

点评数列有形如Sn=f(n)或Sn=f(an)的关系,可考虑用求差Sn−Sn−1=an后,再用其它初等方法求得an,但要检验s1=a1,一定要先分n=1和n≥2两种情况分别进行运算,然后验证能否统一.本题进行了二次化归,第一次把数列化归为等比数列,第二次把数列化归为等差数列.随着化归的逐步进行,问题好解决了.
总之,构造等差数列或等比数列来求数列的通项公式,是求通项公式的重要方法也是高考重点考查的思想,随着试题的千变万化,构造方式也会跟着千差万别,要具体问题具体分析,需要我们反复推敲归纳,通过构造化归为基本数列来解决,在平时教学中要有效训练、积极探索.
巩固练习
2017福建省单科质检理科12题已知数列{an}满足a1=b1=1,an+1=an+2bn,bn+1=an+bn,则下列结论正确的是( )

解此题由题意不难得到:


