借力“会算”、“巧算”,处理选择题
陕西省西安市临潼区马额中学(710609) 童永奇
借力“会算”、“巧算”,处理选择题
陕西省西安市临潼区马额中学(710609) 童永奇
高考数学选择题一般属于容易题和中档题,个别题属于较难题,它的分值占全卷的40%.解选择题的快慢和成功率的高低对于能否使学生进入最佳状态,以至于使整个考试成功与否起着举足轻重的作用.解答数学选择题的基本要求是:准确、迅速、灵活;基本原则是:小题巧解,小题小做.基于此,本文着重说明求解选择题的两个常用解题策略—力求“会算”、“巧算”,以帮助读者拓宽解题思维,进一步提高分析、解决此类问题的实际能力.
策略一、力求“会算”
求解数学中的选择题,最基本、最常用的解题策略就是将之看作解答题,要求学生能够将所学数学知识、方法在解题中加以灵活、综合运用,简言之,就是要求学生“会算”.
1.掌握基本知识,加强“会算”


评注遇到与指数式、对数式有关的比较大小问题时,需要关注指数、对数函数的单调性在解题中的灵活运用.此外,要注意特殊数字“0”、“1”等在比较大小中的桥梁作用.
牛刀小试1设集合A={(x,y)|y=2x+1,x,y∈R},B={(x,y)|x2+(y−a)2=5,x,y∈R},若集合A∩B恰有2个子集,则实数a=( )
A.4或6 B.4或−6 C.6或−4 D.−4或−6
2.掌握常用技巧,加强“会算”


评注本题主要考查三角恒等变换以及三角函数的单调性.方法一侧重于“弦变切”加以灵活处理;方法二侧重于“切变弦”加以灵活处理.本题作为选择题,最简单的解法就是利用“排除法”:取故检验各选项可知只能选B.
牛刀小试2 已知 tanθ=2,则 sin2θ+sinθcosθ−2cos2θ=( )

3.掌握常用方法,加强“会算”
例3已知函数f(x)=x2−2(a+2)x+a2,g(x)=−x2+2(a−2)x−a2+8,H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)},max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值,记H1(x)的最小值为A,H2(x)的最大值为B,则A−B=()
A.a2−2a−16 B.a2+2a−16
C.−16 D.16
解析由题设易知f(x)顶点坐标为(a+2,−4a−4),g(x)顶点坐标(a−2,−4a+12),并且每个函数的顶点都在另一个函数的图象上,如下图所示.显然,A、B分别为两个二次函数顶点的纵坐标,所以A−B=(−4a−4)−(−4a+12)=−16.故选C.
评注本题是一个比较典型的类型,属于考查多元“谁大谁小”类函数最值问题,对学生“画图”、“用图”分析、解决问题的实际能力的考查比较深刻.

图1
牛刀小试3 已知偶函数y=f(x),x∈R满足f(x+1)=−f(x),且当x∈[0,1]时,f(x)=1−x2.若函数则当x∈[−3,4]时,函数y=f(x)−g(x)的零点共有( )
A.4个 B. 5个 C. 6个 D. 7个
策略二、力求“巧算”
由于数学中的选择题具有“四选一”的特点,且不需要给出完整、具体的解题过程,而只需要给出正确的选项即可,所以我们可以考虑这些因素,努力学会“巧算”.
1.借助特例,学会“巧算”
例4 如图,质点P在半径为2的圆周上逆时针运动,其初始位置为角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为( )
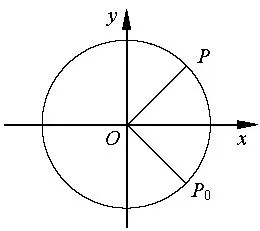
图2

解析本题涉及质点的运动,可以结合质点运动的特殊位置与函数图象之间的联系来确定选项.当t=0时,点P到x轴的距离为排除A,D;由角速度为1知,当时,点P在x轴上,即点P到x轴的距离为0,排除B,故选C.
评注一般地,要说明结论正确,则必须给出证明;要说明结论错误,则只需找到一个反例即可.
牛刀小试4 设[x]表示不大于x的最大整数,则对任意实数x,y,有( )

2.借助画图,学会“巧算”




图3
牛刀小试5已知一元二次不等式f(x)<0的解集为则f(10x)>0的解集为( )
A.{x|x<−1或x>lg2}B.{x|−1<x<lg2}
C.{x|x<lg2}D.{x|x>−lg2}
3.借助规律,学会“巧算”
例6已知椭圆的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,−1),则E的方程为( )
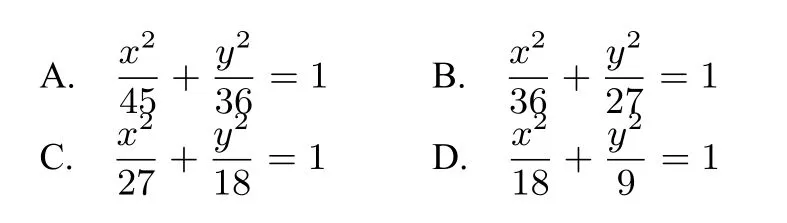

综上,关注数学选择题的常用解题策略,有利于从理论上指导解题实践,有利于不断积累解题经验,逐步提升解题技能.
附:牛刀小试参考答案
1.C.解析:集合A∩B恰有2个子集,即集合A∩B中恰有1个元素,亦即直线2x−y+1=0和圆x2+(y−a)2=5相切.从而,由可得a=6或−4.
2.D.解析:因为

故选D.
3.B.解析:因为f(x+1)=−f(x),所以f(x+2)=−f(x+1)=−[−f(x)]=f(x),所以函数f(x)的周期为2.如图,画出函数f(x)与g(x)的图象,由图可知两图象在[−3,4]内共有2+3=5个交点.故当x∈[−3,4]时,函数y=f(x)−g(x)的零点共有5个.
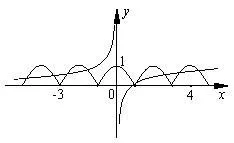
图4
4.D.解析:取x=1.2,则因为 [−x]=−2,−[x]=−1,所以选项A错误.
取x=1.5,则因为[2x]=3,2[x]=2,所以选项B错误.
取x=1.2,y=1.8,则因为[x+y]=3,[x]+[y]=1+1=2,所以选项C错误.
综上,由排除法即知应选D.



图5

