对向量的数量积定义的思考

北京市顺义牛栏山第一中学(101301) 张传海 胡亚萍

对向量的数量积定义的思考

北京市顺义牛栏山第一中学(101301) 张传海 胡亚萍

平面向量的数量积是高中数学知识中的一个核心内容,是学习空间向量知识的基础,能运用它解决一些实际问题、推导其它的公式,这个知识还有很丰富的思想价值和方法价值;对于将来学习高等数学、高等物理学有重要的作用.本内容是必修四第四章第四单元,教材安排两小节.第一小节2.4.1是《平面向量数量积的物理背景及其意义》,类比于物理学功的概念引入过来.在物理学上如果一个物体在力F的作用下产生位移s,那么力F所做的功W=|F||s|cosθ(其中θ是F与s的夹角).类比功的概念,引入“数量积”的概念.

已知两个非零向量a与b,我们把数量|a||b|cosθ叫做a与b的数量积(或內积)记做a·b,即a·b=|a||b|cosθ,规定零向量与任意向量的数量积为零.并解释了其几何意义,介绍了运算律.

第二小节2.4.2《平面向量数量积的坐标运算、模、夹角》,在本节课的开头的探讨中提出:已知两个非零向量a=(x1,y1),b=(x2,y2),怎样用a,b的坐标表示a·b呢?

解答过程如下:因为a·b=(x1i+y1j)·(x2i+y2j)=x1x2i2+x1y2i·j+x2y1i·j+y1y2j2又因为i·i=1,j·j=1,i·j=j·i=0,所以a·b=x1x2+y1y2于是乎由于a·b=|a||b|cosθ,a·b=x1x2+y1y2,所以|a||b|cosθ=x1x2+y1y2,然后就有了夹角公式

一切看似顺理成章,尽善尽美,无懈可击.记下来,背熟了能应用,好像就可以了.因为教材也就这样,没有更深入的解释.

作为一个中学教师,在授课的过程中,以为这样就足够了,实际上留下了一个大的隐患.当学生熟稔这个知识后,如果有心,细致观察式子a·b=|a||b|cosθ=x1x2+y1y2,发现这个式子似乎蒙着一层厚厚的迷雾,感觉这个知识系统似乎并不牢靠,随时可能会崩塌.下面我们来细致分析结论得出的过程.

a·b=x1x2+y1y2是运用向量的运算求出来的,a·b=|a||b|cosθ实实在在;却是类比于物理知识引入过来,给人的感觉就如同是规定;并利用这个等式作为桥梁,得到|a||b|cosθ=x1x2+y1y2,再然后又是具体的向量运算得到代入a·b=|a||b|cosθ再经过变形得出夹角公式:

反观这个过程,给人一种真真假假,虚虚实实的感觉,好像这个系统的一个支架存在巨大问题,这个知识的信度低,进而产生抵触.那么,问题的症结在哪儿呢?容易发现,问题集中在式子|a||b|cosθ=x1x2+y1y2的可靠性上,能否有一个直接的运算来证明它呢?因此,必须要弄清楚这个问题.如何解释这个问题呢?

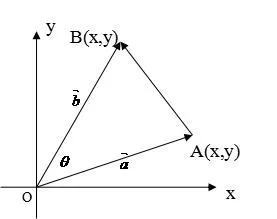
图1

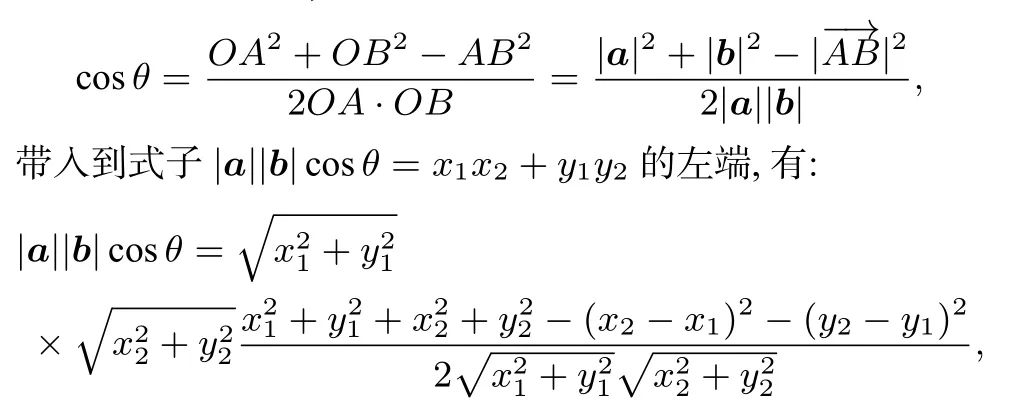
在△OAB中,根据余弦定理有:

化简恰好得到式子x1x2+y1y2.

难道是巧合吗?向量的运算里竟暗含着余弦定理.向量的知识是人们在生产生活的实践中抽象出来,为了解决实际问题而定义的,并经过了大量的事实证明是正确的.这背后的支撑居然是余弦定理,是不谋而合?还是人们引入数量积时遵循了余弦定理,并把它嵌入其中,成为向量知识的骨骼,支撑着这个知识系统,是有意为之?数学知识真是太美妙了!这就是我这里要讲的:向量的数量积背后的故事——余弦定理.