双变量不等式求参数问题的解题策略

广州大学附属中学(510006) 吴坚

双变量不等式求参数问题的解题策略

广州大学附属中学(510006) 吴坚

不等式求参数问题是函数与导数知识在高考中考查的常见命题形式,基本模型为F(x,a)≥G(x,a)(或变形为ψ(x,a)≥0),不少文章都对该类问题的解题方法进行过梳理与总结,本文不再赘述.事实上,在不等式求参数问题中还有一类关于双变量不等式求参数问题,在高考中也不时出现,比如2015年全国II卷第(21)题,该类问题在高三复习备考中并没有引起足够的重视,关于此类的文章亦不多.

作者梳理了2004年到2016年全国各地的高考试卷,将双变量不等式求参数问题的解题策略整理归纳为“一个模型”,“两类关系和状态”,“四种转化”和“两大思想”.

一、一个模型即基本模型为ψ(x1,x2,a)≥ 0或F(x1,x2,a)≥G(x1,x2,a).

二、两类关系指双变量x1,x2是否具有等量关系.如果存在等量关系,则通过消元代换将二元不等式转化为一元不等式;如果不存在等量关系,则观察双变量不等式的特征,判断是否可以通过作商或作和x1+x2、整体代换的方法将二元不等式转化为一元不等式.

例1.(2004年重庆)设函数f(x)=x(x−1)(x−a),a＞1.

(1)求导数f′(x);并证明f(x)有两个不同的极值点x1,x2;

(2)若不等式f(x1)+f(x2)≤0成立,求a的取值范围.

分析(1)略;(2)根据条件,对方程f′(x)=0应用韦达定理得出进而通过对恒等变形,代换整理化简得到2a2−5a+2≥0,最终求得a的取值范围.这一处理技巧还应用在2014年湖南卷第22题中.

如果双变量x1,x2的取值不存在等量关系,请看下例.

例2. (2010湖南理数)已知函数f(x)=x2+bx+c(b,c∈R)对任意的x∈R,恒有f′(x)≤f(x).

(I)证明:当x≥0时,f(x)6(x+c)2;

(II)若对满足题设条件的任意b,c,不等式f(c)−f(b)≤M(c2−b2)恒成立,求M的最小值.

分析(I)证明略;其中由条件f′(x)≤f(x)恒成立转化为二次函数恒成立问题,进而由∆≤0得出这个说明b,c的选取具有任意性,不具有等量关系,而(II)中的不等式化简整理后即c2+bc−2b2≤M(c2−b2),所以本例可以看成关于双变量b,c的不等式求参数问题,上例的解题方法并不适用;认真观察该不等式,可以发现一个重要特征:不等式两边都是关于双变量的二次齐次式.

不失严谨性,先考虑b=0,求得M≥1;当b≠0时,两边同除以b2,即视作的一元二次不等式恒成立问题,需要指出的是的范围,由c≥|b|得出后可分离参数求M范围,或利用二次函数零点分布求M范围,略.

此外上例还可以通过主元思想求解,通过因式分解可将例2(II)中不等式转化为(c−b)(c+2b)≤M(c+b)(c−b),当c=|b|时,恒成立;当c＞|b|时,降次为(c+2b)≤M(c+b),视b为待定参数,c为变量,整理为φ(c)=(M−1)c+Mb−2b≥0对任意的总成立,故M−1＞0且由此解得后略.

三、两类状态指双变量x1,x2是否是分离状态.如果双变量x1,x2可以分离,则将基本模型转化为F(x1,a)≥G(x2,a)问题.

例3.(2010辽宁理数)已知函数f(x)=(a+1)lnx+ax2+1.

(I)讨论函数f(x)的单调性;

(II)设a＜−1.如果对任意x1,x2∈(0,+∞),|f(x1)−f(x2)|≥4|x1−x2|,求a的取值范围.

分析(I)略;(II)本例中双变量x1,x2不存在等量关系,不等式亦非关于的x1,x2齐次式,不能通过整体代换转化为一元不等式.

四、双变量分离状态下的四种转化.

对于双变量分离状态下的不等式问题,更一般的情形可以概括为以下四小类:

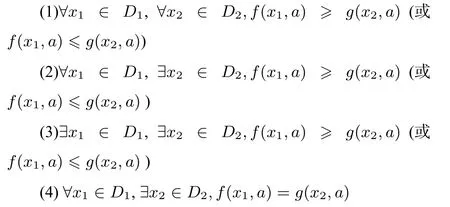
例4. (2010山东理数)已知函数f(x)=lnx−ax+

(II)设g(x)=x2−2bx+4.当a=时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.

分析(I)略;(II)问题转化为f(x1)min≥g(x2,b)max,其中由(I)的单调性分析可知则需对b分类讨论求解,进而求得b的范围.

事实上第(1)类问题等价转化为f(x1,a)min≥g(x2,a)max;第(2)类问题等价转化为f(x1,a)min≥g(x2,a)min;第(3)类问题转化为f(x1,a)max≥g(x2,a)min;第(4)类问题转化为{y|y=f(x1,a),x1∈D1}⊆{y|y=g(x2,a),x2∈D2}.

这四小类问题的转化还可以用主元思想来理解,以(1)为例,固定x2,不等式理解成∀x1∈D1,f(x1,a)≥g(x2,a)(视作固定值),即转化为f(x1,a)min≥g(x2,a),再将不等式理解为∀x2∈D2,f(x1,a)min≥g(x2,a),进而转化为f(x1,a)min≥g(x2,a)max.

当双变量分离状态下的不等式中出现绝对值时,还须通过化归转化思想转化为上述四小类问题.

例5. (2006年湖北卷)设x=3是函数f(x)=(x2+ax+b)e3−x(x∈R)的一个极值点.

(I)求a与b的关系式(用a表示b),并求f(x)的单调区间;

(II)设a＞0,g(x)=若存在ξ1,ξ2∈[0,4]使得|f(ξ1)−g(ξ2)|＜1成立,求a的取值范围.

分析不等式“存在ξ1,ξ2∈[0,4],使得|f(ξ1)−g(ξ2)|＜1”转化为“存在ξ1,ξ2∈[0,4],使−1+g(ξ2)＜f(ξ1)＜1+g(ξ2)”, 进 而 转 化 为−1+g(ξ2)min＜f(ξ1)max且f(ξ1)min＜1+g(ξ2)max,从而求得a的范围.

如果分析f(x)和g(x)在 [0,4]上值域,可以得出g(x)≥f(x),对∀x∈[0,4]恒成立,因此“存在ξ1,ξ2∈[0,4]使得|f(ξ1)−g(ξ2)|＜1”只须使g(x)min−f(x)max≤1,从而求得a的范围.这也体现出教有法而无定法,须适时变通.

五、两大思想——主元思想和化归转化思想

通过上述分析可看出:主元思想和化归转化思想是解决双变量不等式求参数问题的两大思想.“主元思想”,固定其中一个变量(不妨设),把双变量不等式问题构造成另一个变量x2的函数,再从函数角度分析;化归转化思想体现在将复杂的问题转化、分解为简单的、熟悉的问题.

综上所述,对于双变量不等式问题,须识别基本模型,根据两类关系和状态确定范式,选用对应的解题策略,灵活运用主元思想和化归转化思想.从宏观解题策略上来说,将二元不等式转化为单元不等式是其核心,从微观解题策略上来说,包括使用消元代换,整体代换,分离转化、分步转化,逐步调整等技巧,最终通过函数方法解决,以下三个练习供读者参考.

1.(2014湖南)已知常数a＞0,函数f(x)=ln(1+ax)−

(1)讨论f(x)在区间(0,+∞)上的单调性;

(2)若f(x)存在两个极值点x1,x2,且f(x1)+f(x2)＞0,求a的取值范围.

(I)讨论f(x)的单调性;

(II)若f(x)有两个极值点x1,x2,记过点A(x1,f(x1)),B(x2,f(x2))的直线的斜率为k,问:是否存在a,使得k=2−a?若存在,求出a的值,若不存在,请说明理由.

3.(2004全国卷节选)已知函数g(x)=xlnx,设0＜a＜b,证明