区间数分级决策的特征选择方法研究

宋 鹏，梁吉业，钱宇华，李常洪

(1.山西大学经济与管理学院，山西 太原 030006; 2.山西大学计算智能与中文信息处理教育部重点实验室，山西 太原 030006)



区间数分级决策的特征选择方法研究

宋 鹏1,2，梁吉业2，钱宇华2，李常洪1

(1.山西大学经济与管理学院，山西 太原 030006; 2.山西大学计算智能与中文信息处理教育部重点实验室，山西 太原 030006)

在多属性决策分析中，科学的特征选择方法有利于提取关键决策指标，进而求解决策方案并提升决策效率。本文面向区间数分级决策问题，以区间数优势关系为序化信息刻画的基本手段；基于粗糙集与信息熵理论，通过分析条件属性与决策属性序相关性的决策内涵，提出了一种新的特征评价函数——区间序补集条件熵。在此基础上，基于区间序补集条件熵的变化程度，给出了必要属性的形式化表示与属性重要度的度量准则，进而设计了区间数分级决策表的启发式特征选择算法。最后，通过两个案例研究，验证了特征选择方法的有效性。

区间数; 分级决策; 特征选择; 补集条件熵

1 引言

在管理科学与决策科学的发展进程中，多属性决策作为其重要组成部分，也取得了诸多重要的研究成果[1-6]。就多属性决策而言，其可分为选择、排序、分类/分级三大类研究问题[7-8]。然而，需要指出的是，尽管相关研究将分类/分级问题归入了同一类别，但本质上，分类与分级问题具有显著区别。在分类问题中，类别之间没有等级关系；而分级问题，其类别之间具有优劣关系，即有序的分类。实际上，分级决策(Sorting decision)广泛的存在于决策实践中，如能源效率评价、风险评级、城市评价、企业效益评价、组织冲突分析等[9-13]。

在分级决策中，决策者需要基于相关的评价指标集(或称特征集、属性集等)，着眼于问题求解的决策目标，进而对备选方案开展决策分析研究。然而，在众多的评价指标中，往往存在不相关或冗余的属性。这些不相关或冗余的指标，不仅仅会增加决策成本，也将影响决策性能。当然，这也是多属性决策的共性问题。为了有效提升决策性能与决策效率，旨在挖掘符合决策目标的关键特征的特征选择方法受到了更多的关注[14-17]。

就特征选择方法而言，其一般可分为两大类：封装式(Wrapper)、过滤式(Filter)。比较而言，前者在进行特征选择时需结合随后的学习算法来评价候选的特征子集；后者则基于特定的评价函数，通过考查特征之间、特征与决策目标之间的关联程度，从而求解关键特征子集。从决策分析的内涵目标来看，紧密围绕决策问题目标，进而获取重要的特征子集，更有利于决策者在决策全流程中的监督和控制，因此，本文重点探讨过滤式特征选择方法。

就过滤式方法而言，特征评价函数的选择是核心环节。从现有研究进展来看，为了保证特征选择效果，人们从不同视角尝试不同的特征评价函数，如距离度量、依赖性度量和信息度量等[18]。在上述特征评价函数中，基于信息度量的特征评估准则，由于其无需假设数据分布已知，且能够考查特征间的非线性关系，因此，在特征选择方法的研究中备受关注[16, 19-20]。需要进一步强调的是，由于粗糙集方法能够在保持分类能力不变的条件下有效开展属性约简并提取决策规则，因此，基于粗糙集与信息熵结合的特征选择方法的研究成果也不断涌现。Jensen 和 Shen Qiang[21]着眼于保持决策语义不变的视角，提出了粗糙特征选择方法和模糊粗糙特征选择方法。针对经典粗糙集方法需要进行数据离散化的预处理步骤进而引致信息损失的问题，Parthaláin和 Shen Qiang[22]基于相容粗糙集模型给出了一种可以处理连续性数值的特征选择算法。面向特征选择方法计算耗时的共性困难，Qian Yuhua等[23]基于正向近似概念，针对Shannon熵、补集条件熵、组合熵等不同的特征评价函数给出了一类通用的特征选择加速方法。面对实际决策环境中，数据样本呈现动态增加形式的现实问题，Liang Jiye等[24]通过分析信息熵的增量机制提出了一种具有批增量处理能力的粗糙特征选择算法。Tseng和 Huang[25]则将基于粗糙集的特征选择方法应用于客户关系管理研究中。可以看出，基于粗糙集与信息熵结合的特征选择方法为有效提升特征选择的决策性能与计算效率提供了一条可行的研究路径。

需要进一步指出的是，在现实的决策分析中，由于决策问题的不确定性以及决策者的不同偏好，人们面对的数据形式也往往呈现模糊值、缺省值、区间值等复杂形式[26-31]。相应地，相关学者围绕不同的数据表示形式开展了系列的特征选择方法研究。Hu Qinghua等[32]面向具有名义型、数值型和模糊型混合数据的决策表，运用粗糙集模型和模糊粗糙集模型，给出了基于条件熵的特征选择方法。Qian Yuhua等[33]针对模糊型数据的决策表提出了一种特征选择的加速算法。事实上，在实际的决策问题中，各类决策指标的数值往往呈现动态波动的状态，因此，与单值型数据相比，区间型数据更有利于反映数据集的取值情况。因而，基于区间数据的决策建模与分析研究日益受到重视。刘小弟等[34]运用相对熵方法，针对属性取值、方案偏好为区间型数据表示形式的多属性决策问题，开展了群决策建模与分析研究。梁燕华等[35]结合灰靶思想，构建了区间数灰靶决策模型，进而为具有多决策对象、分类数不确定等复杂特性的分类决策问题提供了有效的决策分析方法。郭崇慧和刘永超[36]围绕分类决策问题，基于距离度量区间数的相似性，运用最近邻分类器，建立了一种区间型符号数据的特征选择方法。然而，从现有研究进展来看，关于区间数据分级决策的特征选择研究仍鲜有报道。因而，本文将面向区间数分级决策问题，在粗糙集理论框架下，提出一个新的概念——区间序补集条件熵，通过有效刻画特征集合与有序决策类之间的序的相关性，进而构建一种面向区间数分级决策表开展特征选择的新方法。

2 区间数分级决策表

一般地，称S=(U,AT,V,f)是一个信息系统，其中，U为对象集合，AT为属性集合，V=∪a∈ATVa(Va为属性a的值域)，f:U×AT→V是一个函数使得f(x,a)∈Va(a∈AT,x∈U)。进一步地，称S=(U,AT,V,f)是一个区间信息系统，其中，Va为区间数的集合，f(x,a)的形式表示如下：

f(x,a)=[aL(x),aU(x)]={p|aL(x)≤p≤aU(x),aL(x),aU(x)∈R}.

定义2.1对于区间信息系统S=(U,AT,V,f),若所有的属性均为有序型属性，则称其为一个区间序信息系统。

在区间序信息系统中，有序型属性一般包括收益型属性与成本型属性，对象之间的优劣关系通过优势关系来刻画。

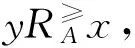
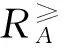
(1)

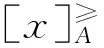
(2)

在此基础上，可以给出区间数分级决策表的定义。

定义2.3称S=(U,C∪d,V,f)是一个区间数分级决策表，若条件属性集C中的属性均是有序型属性且VC为区间数的集合，决策属性为有序的类且f(x,d)∈Vd(x∈U)为单值型数据。

在分级决策表中，可令决策类集合D={D1,D2,…,Dt}(t≤|U|, |·|表示基数)，表示对象集合被划分为t类，即|Vd|=t；进一步地，不失一般性，可令r,s∈T(T={1,2,…,t})，并假设若r>s,则决策类Dr中的对象在决策属性上优于决策类Ds中的对象，而任一决策类内的所有对象则具有同等的优劣级别。

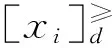
(3)

3 区间序补集条件熵及其特征评价性能

从区间数分级决策表特征选择的决策语义来看，其本质上是在条件属性集上求解与决策属性具有“序的相关性”的属性子集。这里的相关性，可以理解为序的一致性和不一致性。在分级决策表中，所谓序的一致性是指，若对象y在条件属性集A上优于对象x,则对象y在决策属性d上也应优于对象x；反之，若对象y在条件属性集A上优于对象x,而对象y在决策属性d上却不优于对象x,则认为其在序上具有不一致性。

事实上，分级决策表中序的一致性与序的不一致性，共同构成了序的不确定性。从现有研究成果来看，熵可以作为信息系统中不确定性度量的有效工具。本节将基于粗糙集与信息熵的结合，首先给出区间序补集条件熵的定义，然后对其所具有的特征评价性能进行分析。

3.1 区间序补集条件熵

(4)

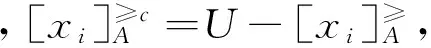
实际上，Liang Jiye等[37]在等价关系条件下，通过考虑等价类的补集信息，提出了信息系统中补集信息熵的概念。然而，其并不适用于具有序信息的决策系统。因此，Song Peng等[31]面向区间序信息系统的决策需求提出了优势关系下的补集信息熵概念。

(5)

根据区间序信息系统中补集信息熵、补集联合熵的定义，可以得出补集条件熵的定义。

定义3.3[31]设S=(U,AT,V,f)是一个区间序信息系统，A,B⊆AT,属性集A关于属性集B的补集条件熵的定义为：

(6)

根据式(6)，可以得出区间数分级决策表的区间序补集条件熵的形式化表示。

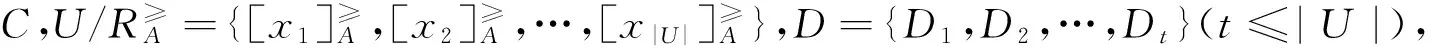
(7)

性质3.1设S=(U,C∪d,V,f)是一个区间数分级决策表，A⊆C,则E(d≥|A≥)=E(d≥∪A≥)-E(A≥)。

证明：根据定义3.4，可以得出

证毕。

从性质3.1可以看出，式(7)所提出的补集条件熵可以度量条件属性集A和决策属性d的联合熵与条件属性集A的信息熵之间的差异，因此，其符合条件熵的内涵。

3.2 区间序补集条件熵的特征评价性能分析

基于区间序补集条件熵的概念表示，本节将首先给出两个重要的定理，然后对其决策语义进行相关分析。

证明见附录A。

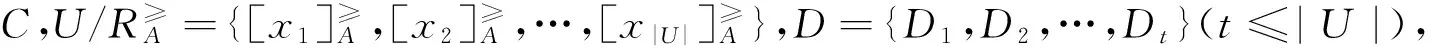
0≤E(d≥|A≥)≤1-1/|U|-E(A≥)

证明见附录B。

可以看出，定理3.1分析了区间序补集条件熵的单调性，定理3.2则分析了其极值性。为了更好地理解极值性，本节将给出性质3.2。

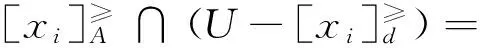
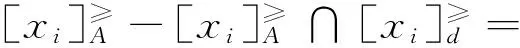
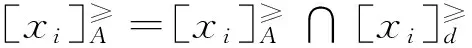
证毕。

4 特征选择方法

就特征选择方法而言，其一般包括初始特征子集的选择、搜索策略、特征评估准则以及停止条件四个方面的内容。在粗糙集理论框架下，特征选择也被称作为属性约简，其是在保持决策能力不变的条件下求解关键属性。相应地，基于区间序补集条件熵的变化程度，本节将建立区间数分级决策的特征选择算法。

在粗糙集理论框架下的属性约简过程中，若从条件属性集中剔除某一属性而条件熵不变，则认为这一属性对于决策而言是不必要的；与之相反，当剔除掉某一属性时条件熵发生变化，则认为这一属性对于决策而言是必要的，所有必要的属性构成的集合也被称作为核。显然，由于核属性对于决策而言是必要的，因此，其构成了特征选择中的初始特征子集。其形式化表示见定义4.1。

定义4.1设S=(U,C∪d,V,f)是一个区间数分级决策表，对于属性c(∀c∈C)，若其满足

E(d≥|(C-c)≥)≠E(d≥|C≥)

(8)

则称属性c为必要属性；若其满足:

E(d≥|(C-c)≥)=E(d≥|C≥)

(9)

则称属性c为不必要属性。

以初始特征子集为特征搜索的基础，基于补集条件熵的变化程度度量剩余属性的重要性程度，将最重要的属性优先进入关键特征子集，进而构建一个启发式搜索策略。为了度量属性重要性程度，需给出区间序补集条件熵的另一性质。

性质4.1设S=(U,C∪d,V,f)是一个区间数分级决策表，对于属性集A(A⊆C)和属性c(c∈C,c∉A)，有E(d≥|A≥)≥E(d≥|(A∪c)≥)。

证毕。

根据性质4.1，基于补集条件熵的变化程度，可给出属性重要性程度的度量准则。

定义4.2 设S=(U,C∪d,V,f)是一个区间数分级决策表，A⊆C,属性c∈C-A,则属性c的重要度为：

Sig(c,A,d)=E(d≥|A≥)-E(d≥|(A∪c)≥)

(10)

当关键特征子集B相对于决策属性的补集条件熵E(d≥|B≥)与E(d≥|C≥)相等时，则说明所搜索到的特征子集保持了原始决策表的决策信息。进一步地，基于必要属性的定义，检测所搜索到的特征子集是否具有冗余属性。即若∀c∈B,满足

E(d≥|(B-c)≥)≠E(d≥|B≥)

(11)

则称关键特征子集B中没有冗余属性。此时，称属性集B为相对于决策属性d的约简。

基于上述分析，可以给出区间数分级决策的特征选择算法。具体算法步骤如下：

步骤1：计算区间数分级决策表S=(U,C∪d,V,f)的区间序补集条件熵E(d≥|C≥)；

步骤2：令特征子集Red←∅,对于条件属性集中的任意属性c∈C,若E(d≥|(C-c)≥)≠E(d≥|C≥),则Red←Red∪{c}；

步骤3：B←Red；

步骤4：计算E(d≥|B≥)；若E(d≥|B≥)≠E(d≥|C≥),则执行步骤5；若E(d≥|B≥)=E(d≥|C≥),则执行步骤6；

步骤5：对属性集C-B循环执行：

5.1：对于任意的属性c∈C-B,计算属性重

要度Sig(c,B,d)；

5.2：若属性c0满足条件Sig(c0,B,d)=max

{Sig(c,B,d),c∈C-B},则B←B∪{c0}；

5.3：若E(d≥|B≥)=E(d≥|C≥),则执行步骤6；若E(d≥|B≥)≠E(d≥|C≥),则转至5.1；

步骤6：对于任意的属性c∈B,若E(d≥|(B-c)≥)=E(d≥|B≥),则B←B-{c}；

步骤7：Red←B,结束。

5 案例研究

在现实的数据挖掘与决策分析任务中，数据的预处理步骤(如缺省数据处理、异常样本剔除、特征选择等)是决策结果的重要影响因素，就其工作量而言，也往往占据决策任务的80%[38]。事实上，Roy[39]将多属性决策分为选择、排序、分类/分级、特征选择四类主要的决策分析任务。可见，特征选择在多属性决策中具有重要的研究意义。本节将面向风险投资项目决策、股票选择决策两个典型的投资决策问题，基于所提出的特征选择方法进行预处理，分别就特征选择与分级决策、特征选择与排序决策的结合开展应用研究。

5.1 风险投资项目决策

从风险投资项目决策的现有研究进展来看，主要围绕投资前的项目筛选开展多属性决策分析研究。然而，为了有效降低投资风险，风投资金往往并非一次全部注入风险项目，而是采取多阶段投资形式。在每一阶段中，可以根据项目的收益情况进行相关决策分析。

表1列示了16个待评价的风险项目。按照项目在上一轮投资后的收益情况分为优、良、一般三类，不失一般性，令决策属性值分别为3、2、1。一般地，在风投专家进行投资前项目筛选时，重点关注管理团队能力、市场竞争力、产品差异度以及财务能力等；在分阶段注入投资后，由于风投企业将参与项目运作与管理(即投资后管理)，因此，主要关注市场竞争力、项目发展能力，并更为细致的考查项目的财务能力。表1列示了8个评价指标cj(j=1,2,…,8)，分别代表市场销售能力(销售毛利率)、项目发展能力(资产增长率)、项目现金流能力(经营活动现金流比率、现金流动负债比率)、项目营运能力(总资产周转率、固定资产周转率)、项目抵御财务风险能力(速动比率、利息保障倍数)。

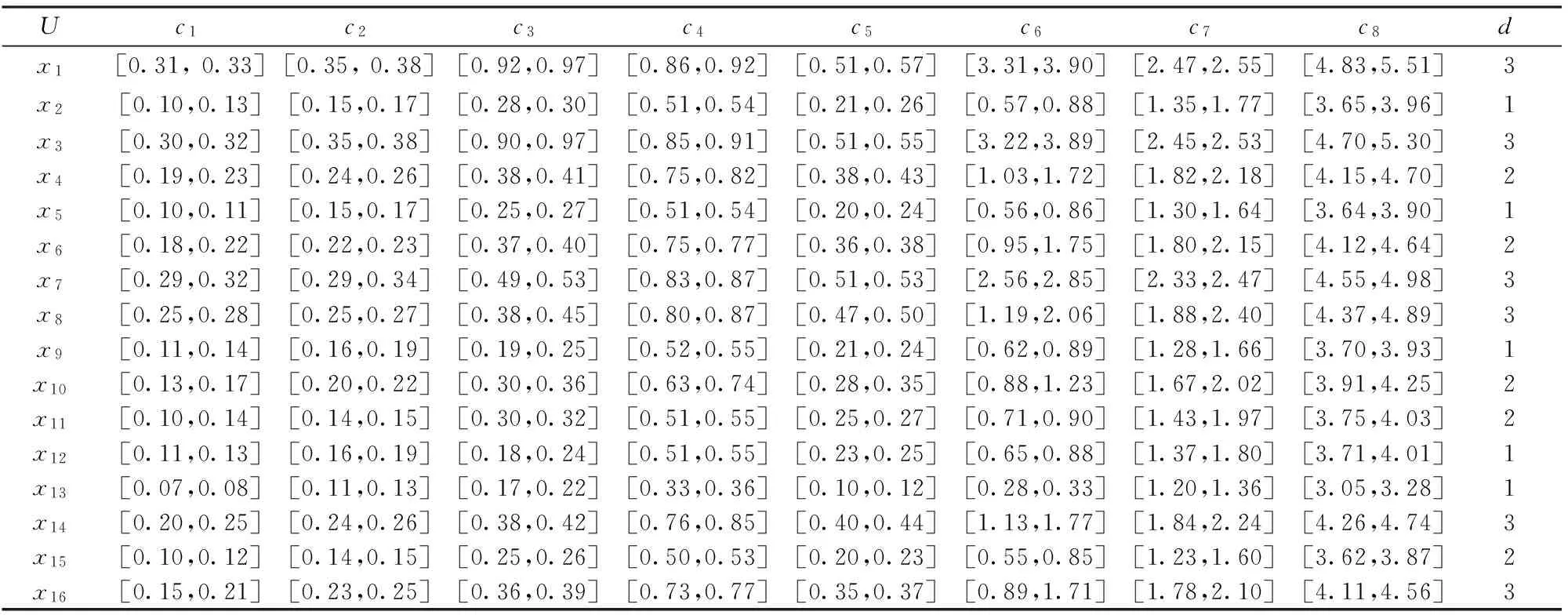
表1 风险投资项目决策指标值数据表

就风险投资项目的多阶段投资模式而言，在每一投资阶段的项目运行中，项目运营业绩指标的数值往往呈现动态波动的特征。一般地，决策者往往以每一阶段为特定时间段来计量相关的业绩指标；相应地，获得的指标数值则是单值数据形式，并以此为基础进行决策分析。显然，单值数据难以反映现实中各项业绩指标的取值波动情况。为了更好地刻画数据的数值波动特征，可将每一投资阶段按照特定标准(如月份、季度)划分为多个时间段，并针对每个时间段计算相应的指标数值；在此基础上，通过分析每一指标不同时间段的多个数值的取值情况，给出该指标的区间数值。本文基于数据打包思想[40]，以每一指标数值的最小值为区间值下界，以每一指标数值的最大值为区间值上界，进而给出每一指标的区间数。当然，需要说明的是，当每一指标的数据样本足够多时，则可通过估计数值的分布，给出更为准确的区间数取值。基于上述思想，结合我国高科技行业相关指标的实际取值范围，表1给出了16个风险项目的8个评价指标的区间数据。

按照算法，可以得出如下特征选择计算结果。

(1)计算表1的区间序补集条件熵，可得E(d≥|C≥)=0.0078。

(2)针对每个指标计算E(d≥|(C-c)≥),可得：

E(d≥|(C-c1)≥)=0.0117,E(d≥|(C-c2)≥)=0.0117

E(d≥|(C-c3)≥)=0.0156

E(d≥|(C-c4)≥)=E(d≥|(C-c5)≥)=E(d≥|(C-c6)≥)=E(d≥|(C-c7)≥)=E(d≥|(C-c8)≥)=0.0078

因此，核属性集为{c1,c2,c3}。

(3)计算核属性集相对于决策属性的区间序补集条件熵，得出:

E(d≥|{c1,c2,c3}≥)=0.0078=E(d≥|C≥)

(4)回溯检验属性集{c1,c2,c3}是否存在冗余属性，可得:

E(d≥|(B-c1)≥)=0.0117≠E(d≥|B≥),

E(d≥|(B-c2)≥)=0.0117≠E(d≥|B≥),

E(d≥|(B-c3)≥)=0.0156≠E(d≥|B≥)。

因此，属性集{c1,c2,c3}中不存在冗余属性。相应地，可得关键特征子集为：

B={c1,c2,c3}

从关键特征子集的决策语义来看，其表示特征子集中的相关指标与决策属性具有序相关性。就风险投资项目的投资后管理而言，探寻与项目收益具有序相关的关键评价指标，可为风险投资项目的运作管理构建重点指标监控体系，并提取分级决策规则。事实上，粗糙集理论的核心思想就是通过有效的特征选择进而获取符合人类决策行为模式的If…then…决策规则。进一步地，结合Qian Yuhua等[41]，可以对决策规则、整体决策规则集的决策性能进行评价。本节仅讨论各规则的决策性能。

根据表1中每个项目的指标数据可以诱导出一条决策规则。首先，可分析决策属性值f(xi,d)=3的项目x1,x3,x7,x8,x14,x16,相应地，基于关键特征子集可获得6条决策规则：

a)Iff(x,c1)≥[0.31,0.33]∧f(x,c2)≥[0.35,0.38]∧f(x,c3)≥[0.92,0.97], thenf(x,d)≥3.

b)Iff(x,c1)≥[0.30,0.32]∧f(x,c2)≥[0.35,0.38]∧f(x,c3)≥[0.90,0.97], thenf(x,d)≥3.

c)Iff(x,c1)≥[0.29,0.32]∧f(x,c2)≥[0.29,0.34]∧f(x,c3)≥[0.49,0.53], thenf(x,d)≥3.

d)Iff(x,c1)≥[0.25,0.28]∧f(x,c2)≥[0.25,0.27]∧f(x,c3)≥[0.38,0.45], thenf(x,d)≥3.

e)Iff(x,c1)≥[0.20,0.25]∧f(x,c2)≥[0.24,0.26]∧f(x,c3)≥[0.38,0.42], thenf(x,d)≥3.

f)Iff(x,c1)≥[0.15,0.21]∧f(x,c2)≥[0.23,0.25]∧f(x,c3)≥[0.36,0.39], thenf(x,d)≥3.

对于每个决策规则而言，可根据其确定度(Certainty measure)对其决策性能进行评价。确定度的形式表示为：

(12)

根据式(12)，可以计算得出上述6条决策规则的确定度，即：

CM(x1)=CM(x3)=CM(x7)=CM(x8)=CM(x14)=100%,

CM(x16)=6/7=85.71%.

进一步分析基于对象x16诱导出的决策规则f，可以发现，存在一个对象x4与其相矛盾，该对象在条件属性上符合决策规则，但其决策属性值却为2。综合来看，由于前5条规则均是完全确定的，因此，可将其合并。实际上，规则e包含了前4条规则。所以，通过分析决策属性值f(xi,d)=3的项目x1,x3,x7,x8,x14,x16,可以得出一条确定性决策规则，一条非确定性决策规则，即：

r1:Iff(x,c1)≥[0.20,0.25]∧f(x,c2)≥[0.24,0.26]∧f(x,c3)≥[0.38,0.42], thenf(x,d)≥3.(CM=100%)

r2:Iff(x,c1)≥[0.15,0.21]∧f(x,c2)≥[0.23,0.25]∧f(x,c3)≥[0.36,0.39], thenf(x,d)≥3. (CM=85.71%)

类似地，通过分析决策属性值f(xi,d)≥2的11个项目，可以得出两条决策规则，即：

r3:Iff(x,c1)≥[0.10,0.14]∧f(x,c2)≥[0.14,0.15]∧f(x,c3)≥[0.30,0.32], thenf(x,d)≥2. (CM=100%)

r4:Iff(x,c1)≥[0.10,0.12]∧f(x,c2)≥[0.14,0.15]∧f(x,c3)≥[0.25,0.26], thenf(x,d)≥2.(CM=91.67%)

可以看出，基于关键特征子集，决策者可获取更为精炼的分级决策规则。实际上，精炼的决策规则在实际的决策分析中是非常必要的，毕竟决策规则中条件属性的数量越多，其在决策支持中的泛化能力(即适用性)就会越弱。进一步地，结合决策规则的确信度评价，可为决策者提供具有概率意义的决策规则评价准则。

当然，需要说明的是，为了便于直观理解，本节通过简洁的算例分析了特征选择、分级决策规则的决策内涵。实际上，在风险投资项目决策的投资后管理中，基于大量、多轮的项目案例，通过分析关键特征子集及其对应的分级决策规则，特别是分析决策规则中各指标的取值分布情况以及各决策规则的平均确信度，有利于风险投资项目的相关利益主体建立多阶段风险投资项目管理的重点指标监控与量化评价体系，进而为风险投资项目决策优化提供有效的决策支持。

5.2 股票选择决策

随着全球资本市场的迅速发展，股票投资决策的研究也受到更为广泛的关注。尤其近二十年来，随着人工智能决策方法的发展，关于选股策略的研究不断涌现。当然，关于选股策略研究的争论也从未停止。有效市场理论认为，投资者在可用信息集(历史的价格信息、市场公开信息以及私有信息)下无法获得超额收益，并将市场划分为弱式、半强式及强式有效三种形式。但是，诸多的研究证据表明中国股票市场未达半强式有效，这也就意味着，投资者基于公开的企业财务信息可以获得超额投资收益。

本节以上证180指数成分股为研究样本，基于9个财务指标(条件属性)以及股票收益率(决策属性)构建区间数分级决策表。基于特征选择算法，可以获取与股票收益率具有序相关性的关键财务指标。在此基础上，通过特定的排序方法，基于关键财务指标集进行排序决策，即可获得股票选择的排序决策结果。本质上来看，这是一类符合谨慎投资者投资需求的股票选择策略。其核心思想是，在影响股票收益率的众多影响因素中(如：财务指标、宏观经济指标、专家投资建议、“内幕消息”等)，只有基于反映企业经济运行情况的评价准则进行的决策，才是可靠的选股策略。Sevastjanov和Dymova[42]以模糊数为数据的基本表示形式，基于上述思想开展了股票选择决策研究。本文则基于区间数据表示形式，综合运用区间数分级决策的特征选择方法和区间数排序决策方法，开展股票选择决策研究。

事实上，从股票选择决策的研究进展来看，决策者往往基于财务指标的单值数据开展决策建模与分析。然而，对于股票市场而言，无论是上市公司的财务指标还是市场回报指标，数值的波动性是普遍而又必须关注的特征。显然，传统的单值数据是一种信息不完全的数据表现形式。相比较单值数据而言，区间数据更有利于反映数值的取值分布情况，更有利于揭示数据取值的整体特性。

本节选取全球金融危机爆发后的2009年上证180指数成分股为研究样本。在样本选择时，考虑到金融类上市公司与非金融类上市公司的财务指标数值具有显著差异，剔除掉了金融类股票；考虑到股票选择决策本质上是选优，剔除掉了企业经营中利润指标为负值的股票；此外，剔除了数据不全的公司。样本股票共91支。财务指标选择了表示企业财务运营状况的常用的9个指标，分别为：营业利润率、净资产收益率、现金流量比率、现金流动负债比率、总资产周转率、固定资产周转率、净利润增长率、速动比率、资产负债率。在构建区间数分级决策表时，基于上市公司的季报公布制度，考虑到上市公司2008年度的财务报告在2009年4月30日前公布，因此，财务指标以2008年度的季度数据为基础，取季度数据的最大值为区间数的上界，取季度数据的最小值为区间数的下界；决策属性则按照2009年5月——6月股票收益率的取值，将样本分为三类，即股票收益率前30%样本的决策属性值为3，股票收益率后30%样本的决策属性值为1，其余样本的决策属性值为2。具体数据信息见表2。

按照算法，可以得出如下特征选择计算结果。

(1)计算表2的区间序补集条件熵，可得：

E(d≥|C≥)=0.000724

(2)针对每个指标计算E(d≥|(C-c)≥),可得：

E(d≥|(C-cj)≥)≠E(d≥|C≥) (j=1,3,5,6,7,9)

E(d≥|(C-cj)≥)=E(d≥|C≥) (j=2,4,8)

因此，核属性集为{c1,c3,c5,c6,c7,c9}

(3)计算核属性集相对于决策属性的区间序补集条件熵，得出：

E(d≥|{c1,c3,c5,c6,c7,c9}≥)=0.001087≠E(d≥|C≥)

(4)计算非核属性的重要度，可得：

Sig(c2,B,d)=0.000363,Sig(c4,B,d)=0.000242

Sig(c8,B,d)=0.000363

可以看出，此时，属性c2和c8的重要度最大，则分别令其进入关键特征子集，并计算区间序补集条件熵，得出：

E(d≥|{c1,c3,c5,c6,c7,c9,c2}≥)=E(d≥|C≥)

E(d≥|{c1,c3,c5,c6,c7,c9,c8}≥)=E(d≥|C≥)

(5)回溯检验属性集{c1,c3,c5,c6,c7,c9,c2}和{c1,c3,c5,c6,c7,c9,c8}是否存在冗余属性，可得各属性此时均满足E(d≥|(B-cj)≥)≠E(d≥|B≥)。因此，可以得出，区间序分级决策表具有两个特征选择结果，即：

B1={c1,c2,c3,c5,c6,c7,c9},B2={c1,c3,c5,c6,c7,c8,c9}

基于特征选择结果，结合文献[31]中的区间数排序决策方法，可以获得股票选择决策的排序结果。表3列示了基于两个关键特征子集的两种排序前5位的股票选择决策结果。可以看出，两种结果中有4支股票是相同的。实际上，在第一种排序结果中代码为600085的股票在第二种排序决策结果中排列于第6位，说明了两个关键特征子集所包含的决策信息是相近的。

表2 股票选择决策指标值数据表

表3 排序前五位股票结果列表

进一步地，为了验证方法的有效性，表4列示了两种方案下持有前五位股票从2009年7月——2009年12月(即持有1个月至持有6个月)的股票平均回报率；为了分析投资策略的收益能力，将同期的上证180指数回报率作为选股策略是否有效的评价基准，并在表4中列示；同时，考虑到研究样本集进行了样本剔除，因此，本文也计算了同期的股票样本集的平均回报率。为了清晰的展示实证结果，图1给出了投资回报率的比较图。从表4与图1的结果可以看出，本节基于特征选择结果构建的股票选择策略可以获得超额收益，进而验证了方法的有效性。

表4 股票回报率结果列表

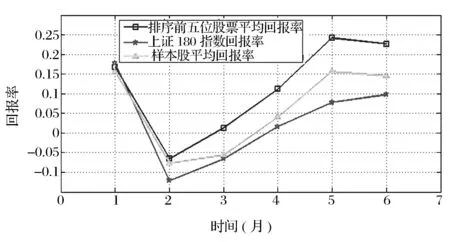
图1 股票回报率结果比较图

6 结语

特征选择作为多属性决策的重要预处理步骤，对于决策分析任务中，有效获取关键决策指标进而求解决策方案、提升决策效率具有重要的意义。本文面向区间数分级决策问题，以区间数优势关系作为区间数分级决策表序化信息刻画的基本手段，基于粗糙集理论与信息熵的结合，着眼于条件属性与决策属性序相关性的度量，提出了一个新的特征评价函数——区间序补集条件熵。在此基础上，通过分析区间序补集条件熵的变化程度，基于必要属性概念给出了初始特征子集的选取方法，基于属性重要性程度的度量准则设计了关键特征子集的搜索策略，进而构建了基于区间序补集条件熵的区间数分级决策表特征选择算法。通过风险投资项目决策与股票选择决策两个案例，说明了特征选择与分级决策、特征选择与排序决策结合的决策建模与分析流程。研究结果表明，本文所提出的区间序补集条件熵可以有效度量条件属性与决策属性的序相关性，进而为区间数分级决策中求解关键决策指标提供了科学的特征选择方法。

附录：

A.定理3.1的证明

证明：根据定义3.4，可以得出

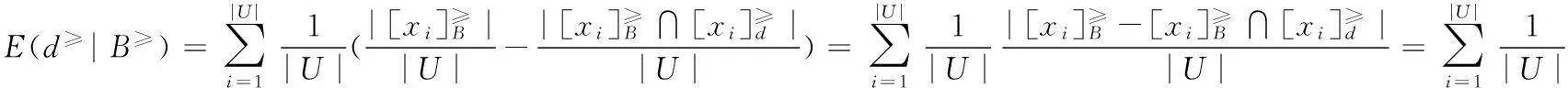
证毕。

B.定理3.2的证明

证毕。

[1] Dyer J S, Fishburn P C, Steuer R E, et al. Multiple criteria decision making, multiattribute utility theory: The next ten years[J]. Management Science, 1992, 38(5): 645-654.

[2] Wallenius J, Dyer J S, Fishburn P C, et al. Multiple criteria decision making, multiattribute utility theory: Recent accomplishments and what lies ahead[J]. Management Science, 2008, 54(7): 1336-1349.

[3] 梁昌勇, 顾东晓, 程文娟, 等. 含非连续性信息多属性案例中的决策知识发现方法[J]. 中国管理科学, 2014, 22(4): 83-91.

[4] 刘健, 刘思峰, 马义中, 等.基于心理阈值的多属性决策问题目标调整研究[J]. 中国管理科学, 2015, 23(2): 123-130.

[5] 丁涛, 梁樑. 基于方案占优和排序稳健性的多属性决策方法[J]. 中国管理科学, 2016, 24(8): 132-138.

[6] 韩菁, 叶顺心, 柴建,等. 基于后悔理论的混合型多属性案例决策方法[J]. 中国管理科学, 2016, 24(12): 108-116.

[7] Roy B.Multicriteria methodology for decision aiding[M]//Pardalos P.nonconvex optimization and its applications.US:Springer Verlag, 1996.

[8] Zopounidis C, Doumpos M.Multicriteria classification and sorting methods: A literature review[J]. European Journal of Operational Research, 2002, 138 (2): 229-246.

[9] Neves L P, Martins A G, Antunes C H, et al. A multi-criteria decision approach to sorting actions for promoting energy efficiency[J]. Energy Policy, 2008, 36(7): 2351-2363.

[10] Kadziński M, Tervonen T, Figueira J R.Robust multi-criteria sorting with the outranking preference model and characteristic profiles[J]. Omega, 2015, 55: 126-140.

[11] Kadziński M, Ciomek K, Sowiński R.Modeling assignment-based pairwise comparisons within integrated framework for value-driven multiple criteria sorting[J].European Journal of Operational Research, 2015, 241(3): 830-841.

[12] 张小芝, 朱传喜, 朱丽. 时序多属性决策的广义等级偏好优序法[J]. 中国管理科学, 2014, 22(4): 105-111.

[13] Silva M M, Costa APCS,de Gusmao APH.Continuous cooperation: Aproposal using a fuzzy multicriteria sorting method[J]. International Journal of Production Economics, 2014, 151: 67-75.

[14] Dash M, Liu Huan.Consistency-based search in feature selection[J]. Artificial Intelligence, 2003, 151(1-2): 155-176.

[15] 赵宇, 黄思明, 陈锐. 数据分类中的特征选择算法研究[J]. 中国管理科学, 2013, 21(6): 38-46.

[16] Lee J, Kim D W.Fast multi-label feature selection based on information-theoretic feature ranking[J]. Pattern Recognition, 2015, 48(9): 2761-2771.

[17] Maldonado S, Montoya R, Weber R.Advanced conjoint analysis using feature selection via support vector machines[J]. European Journal of Operational Research, 2015, 241(2): 564-574.

[18] 姚旭, 王晓丹, 张玉玺, 等. 特征选择方法综述[J]. 控制与决策, 2012, 27(2): 161-166.

[19] Peng Hanchuan, Long Fuhui, Ding C. Feature selection based on mutual information: Criteria of max-dependency,max-relevance, and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8):1226-1238.

[20] Wang Feng, Liang Jiye. An efficient feature selection algorithm for hybrid data[J]. Neurocomputing, 2016, 193(c): 33-41.

[21] Jensen R, Shen Qiang.Semantics-preserving dimensionality reduction:Rough and fuzzy-rough-based approaches[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16(12): 1457-1471.

[22] Parthaláin N M, Shen Qiang.Exploring the boundary region of tolerance rough sets for feature selection[J]. Pattern Recognition, 2009, 42(5): 655-667.

[23] Qian Yuhua, Liang Jiye, Pedrycz W, et al. Positive approximation:An accelerator for attribute reduction in rough set theory[J]. Artificial Intelligence,2010, 174(9-10): 597-618.

[24] Liang Jiye, Wang Feng, Qian Yuhua,et al.A group incremental approach to feature selection applying rough set technique[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(2): 294-308.

[25] Tseng T L, Huang C C.Rough set-based approach to feature selection in customer relationship management[J]. Omega, 2007, 35 (4): 365 - 383.

[26] 徐泽水, 达庆利. 一种基于可能度的区间判断矩阵排序法[J]. 中国管理科学, 2003, 11(1): 63-65.

[27] Xu Zeshui, Liao Huchang.Intuitionistic fuzzy analytic hierarchy process[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(4): 749 - 761.

[28] 樊治平, 陈发动, 张晓. 考虑决策者心理行为的区间数多属性决策方法[J]. 东北大学学报(自然科学版), 2011, 32(1): 136-139.

[29] Fan Zhiping, Liu Yang.An approach to solve group-decision- making problems with ordinal interval numbers[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2010, 40(5):1413-1423.

[30] Liang Jiye, Xu Zongben.The algorithm on knowledge reduction in incomplete information systems[J].International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(1): 95-103.

[31] Song Peng, Liang Jiye, Qian Yuhua. A two-grade approach to ranking interval data[J]. Knowledge-Based Systems, 2012, 27: 234-244.

[32] Hu Qinghua, Yu Daren, Xie Zongxia. Information-preserving hybrid data reduction based on fuzzy-rough techniques[J]. Pattern Recognition Letters, 2006, 27 (5):414-423.

[33] Qian Yuha, Wang Qi, Cheng Honghong, et al.Fuzzy-rough feature selection accelerator[J]. Fuzzy Sets and Systems, 2015, 258: 61-78.

[34] 刘小弟, 朱建军, 刘思峰. 方案有不确定偏好的区间数相对熵群决策方法[J]. 中国管理科学, 2014, 22(6): 134-140.

[35] 梁燕华, 郭鹏, 朱煜明. 基于样本集的区间数灰靶分类决策模型及应用[J]. 中国管理科学, 2014, 22(5): 98-103.

[36] 郭崇慧, 刘永超. 区间型符号数据的特征选择方法[J]. 运筹与管理, 2015, 24(1): 67-74.

[37] Liang Jiye, Chin K S, Dang C Y, et al. A new method for measuring uncertainty and fuzziness in rough settheory[J]. International Journal of General Systems, 2002, 31(4):331-342.

[38] Piramuthu S.Evaluating feature selection methods for learning in data mining applications[J]. European Journal of Operational Research, 2004, 156(2): 483-494.

[39] Roy B.Méthodologie Multicritèred’Aide à la Décision[M]. Paris:Economica, 1985.

[40] Diday E. From data to knowledge: Probabilistic objects for a symbolic data analysis[M]//Dodge Y,Whittaker J.Statistics,Heidelberg:Physica,1992.

[41] Qian Yuhua,Liang Jiye, Song Peng, et al.Evaluation of the decision performance of the decision rule set from an ordered decision table[J].Knowledge-Based Systems, 2012, 36: 39-50.

[42] Sevastjanov P, Dymova L. Stock screening with use of multiple criteria decision making and optimization[J]. Omega, 2009, 37(3): 659-671.

Research on Feature Selection Method for Interval Sorting Decision

SONG Peng1,2，LIANG Ji-ye2，QIAN Yu-hua2，LI Chang-hong1

(1. School of Economics and Management, Shanxi University, Taiyuan 030006, China;2.Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education,Shanxi University, Taiyuan 030006, China)

In the field of multiple attributes decision making, sorting decision has become an important kind of issue and been widely concerned in many practical application areas. In the process of making sorting decision,the rational and effective feature selection methods can extract informative and pertinent attributes, and thus improve the efficiency of decision making. From the extant literatures, many valuable researches have been provided for more reasonably solving this problem in the context of diverse data types, such as single value, null value and set value. However, very few studies focus on the sorting decision in term of interval-valued data. The objective of this paper is to provide a new feature selection approach for interval sorting decision by using the interval outranking relation. By integrating rough set model and information entropy theory, a new measurement called complementary condition entropy, which investigates the complementary nature of the relevant sets, is proposed for feature evaluation through analyzing the inherent implication of correlation between considered attributes in the problem of interval sorting decision. Furthermore,on the basis of the difference of the values of complementary condition entropy,the representation of the indispensable attributes and the measurement of attributes importance are presented, and then develop a heuristic feature selection algorithm is proposed for interval sorting decision. Finally, two illustrative applications, namely,the issues of venture investment and portfolio selection, are employed to demonstrate the validity of the proposed method.For the problem of multi-stage venture investment decision, through investigating the competitiveness, development capacity and financial capability of 16 investment projects, the corresponding probabilistic decision rules having better generalization capability, which can be used to determine whether to perform further investment. As to the issue of portfolio selection, 91 stocks coming from Chinese stock market and 9 operating performance indicators of these firms are employed. By using the presented approach in this study, a portfolio which has better investment return can be construeted. Accordingly, the corresponding strategy for building portfolio is useful to quantitative investment decision. In brief, as the important preprocessing tool in the process of decision analysis, the feature selection method built in this paper is of extensive meaning for discovering the key indicators and improving decision performance in the field of sorting decision.

interval-valued data; sorting decision; feature selection; complementary condition entropy

2016-01-014；

2016-02-12

国家自然科学基金青年项目(71301090)；国家自然科学基金重点项目(71031006, 61432011)；国家优秀青年科学基金项目(61322211)；教育部人文社会科学研究青年基金项目(12YJC630174)；山西省高等学校创新人才支持计划(2013052006)

宋鹏(1979-)，男(汉族)，山西晋城人，山西大学经济与管理学院副教授，管理学博士，研究方向：决策理论与方法、数据挖掘,E-mail:songpeng@sxu.edu.cn.

1003-207(2017)07-0141-12

10.16381/j.cnki.issn1003-207x.2017.07.016

C934

A