基于交叉效率新计算方法的区间效率值排序

成达建，薛声家

(暨南大学管理学院，广东 广州 510632)



基于交叉效率新计算方法的区间效率值排序

成达建，薛声家

(暨南大学管理学院，广东 广州 510632)

考虑了数据包络分析中决策单元区间效率值的计算方法和排序问题。首先，针对交叉效率评价方法中由于交叉效率值不唯一而存在的需要解多个附加的辅助线性规划问题的缺陷，提出通过求传统DEA线性规划模型多个基最优解以获得区间效率值下限的新方法，从而大大减少了计算工作量。然后使用Hurwicz决策准则构建考虑到决策者乐观程度的决策单元区间效率值的排序方法，并进行对于乐观系数的区间效率值排序稳定性分析。最后给出计算例子以说明方法的有效性。

数据包络分析；决策单元；交叉效率；区间效率值；多个基最优解

1 引言

数据包络分析(DEA)是处理多输入和多输出问题的一种非参数方法，它已被广泛应用于非营利组织和营利组织的绩效评估乃至多属性决策问题的方案选择，并应用到输入输出数据是不确定的情形以及需要考虑决策单元内部结构等情形[1-4]。传统的DEA方法单纯依靠自评体系来对决策单元(DMU)进行评价，也就是寻找对受评DMU最有利的输入和输出权重组合，使输出加权平均与输入加权平均的比值最大化。这种从乐观角度计算得出的点效率值容易造成“孤芳自赏”的情形，是不够合理和全面的，因为输入和输出可以有多种权重组合的选取方法。近年来，有不少学者指出[5-7]，各DMU的效率值应有一个可能的变动范围，该范围构成一个效率值区间，其上限是DMU最好的相对效率值(从乐观角度评价)，其下限是最差的相对效率值(从悲观角度评价)，也就是说，DMU具有区间效率值。由于区间效率值能在一个统一的DEA模型框架内给每个DMU以完全的评估，因而会得到比传统点效率值更加全面和深入的结论。

近年来已有不少关于区间效率的研究工作[5-9]，其中的交叉效率评价方法[7-13]很具有代表性。该方法的主要思想是利用自评和互评体系来消除或减轻传统DEA方法中单纯依靠自评体系对决策单元进行评价的弊端，因此引起很多学者的关注并得到长足的发展和广泛的应用。然而，交叉效率评价方法本身仍然存在缺陷，其中最主要的缺点就是最初提出的交叉效率方法由于CCR模型存在可能多个最优解而导致交叉效率值不唯一。针对交叉效率值不唯一的问题及交叉效率值的理论基础，有学者[14]提出了基于交叉评价策略的全局协调相对效率，并基于优化理论给出一个可以用于决策单元优劣排序的全局协调相对效率测度模型；也有学者[15]提出了一种决策单元交叉效率的自适应群评价方法，该方法能得到客观稳定的决策单元交叉效率有效性分值及排序。上述文献深化了对决策单元交叉效率评价方法的探讨。为了解决交叉效率值不唯一的问题，一些文献[7-10]采用了两阶段的计算方法：第一阶段对每个DMU求解传统DEA模型以确定其自评效率值，这个阶段需要解n个线性规划模型(n为决策单元的总数)；第二阶段是求出符合要求的交叉效率值，需要解一系列的线性规划或二次规划，例如王美强和梁樑[7]、吴杰和梁樑[8]为求得交叉效率值，需要解n×(n-1)个附加的线性规划。这样，两个阶段共要解n2个线性规划，可见计算工作量是很大的。

本文基于薛声家和左小德[16]的结果，在第一阶段中增加了求线性规划全部极点最优解(基最优解)的程序，并推导出实用的最小(大)交叉效率值的判别条件，从而避免了第二阶段的执行，这就大大减少了计算工作量。此外，文中还对决策单元区间效率值下限的确定方法及区间效率值的排序方法作了补充和改进，并进行了排序方法的稳定性分析。

2 交叉效率及新计算方法

假设有n个决策单元(DMU)，每个决策单元都有m种输入和s种输出。已知第j个决策单元DMUj(j=1,2,…,n)的输入和输出向量分别为：

Xj=(x1j,x2j, …,xmj)T>0和Yj=(y1j,y2j, …,ysj)T>0

下面的(CCR)d模型可求出对被评价单元DMUd最有利(使其效率值达到最大)的输入和输出权重。

ωi≥0,i=1,2,…,m

μk≥0,k=1,2,…,s其中，决策变量ωi(i=1,2,…,m)和μk(k=1,2,…,s)分别为各输入和输出的对应权重。

在(CCR)d模型中，令d分别取值1,2,…,n，则可以得到所有DMU之最优权重和相应的(最大)效率值。

基于以上CCR模型的最优权重，文献[7-11]定义DMUj使用DMUd的最优权重所获得的交叉效率为：

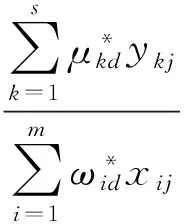
(1)

由于模型(CCR)d的最优解可能不唯一，因此，使用式(1)计算得到的交叉效率值也可能不唯一，为了确定区间效率值的下限，我们必须求出最小交叉效率值。

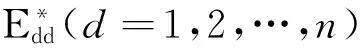
ωi≥0, i=1,2,…,m

本文认为，我们完全可以避免工作量庞大的第二阶段，为此只需要在第一阶段中增加求(CCR)d模型多个最优解的程序。由文献[16]知，线性规划最优解的一般表达式为最优极点(基最优解)的凸组合与最优极方向的非负线性组合之和。由于(CCR)d模型的可行集为有界集，故不存在最优极方向。下面将指出，只需求出(CCR)d数目有限的全部基最优解(仅要作有限次单纯形法的转轴运算，其次数远小于解一个线性规划)，就能确定使交叉效率值最小的最优权重。

把(CCR)d的最优解记为m+s向量

则(CCR)d的最优解一般表达式为：

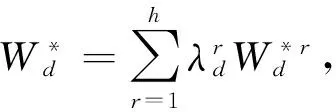
亦即：

(2)

(3)

把(2)和(3)代入式(1)可得：

(4)

记：

(5)

则有：

(6)

设指标t满足：

(7)

(8)

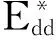
初始步 令d:=1，进入步骤1。

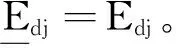
步骤3 求(CCR)d的全部基最优解[16]

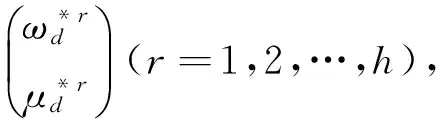
步骤5 若d=n，停止；否则令d:=d+1，返回步骤1。

3 基于区间效率值的决策单元排序

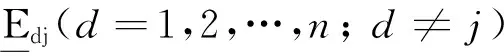
而且绝大多数情形都是严格不等式成立。因此，正确的取法应是:

(9)

关于DMU区间效率值的排序，已有了不少研究，但存在一些不足。吴杰和梁樑[8]的排序方法使用了效率值服从均匀分布于效率值区间的假设，这似乎不很合理，因为区间效率值的上限与下限只是交叉效率或相对效率的极端值，我们没有充分依据说明效率值是等可能性地分布于效率值区间。另一方面，实际工作中决策者对效率值的分布会有一定程度的了解，因而决策单元效率评价引入决策者风险偏好会更加合理。王美强和梁樑[7]采用最小最大后悔值方法进行排序，但这种做法实际上忽略了对各DMU的区间效率值上限的比较，该方法的使用也说明进行排序的决策者是较悲观和厌恶风险的(使用传统的DEA是乐观的排序方法)。实际上，大部分决策者对风险的态度是介于悲观和乐观之间，因此，有必要引入考虑到决策者风险偏好的排序方法。

借鉴赫维茨(Hurwicz)的折衷准则引入乐观系数α(0≤α≤1)来表示排序决策者的乐观程度，作效率折衷值：

(10)

然后根据Hj的大小对各DMU进行区间效率值的排序：若Hj1>Hj2，则DMUj1排前于DMUj2，记作DMUj1≻DMUj2；若Hj1=Hj2，则两DMU排序相同，记作DMUj1～DMUj2。显然，对于不同的α值(对应于不同风险偏好的决策者)，各DMU的排序有所不同。下面讨论排序结果对α变化的稳定性。

假设当α=0(悲观的排序决策者)，有如下的排序：

DMUj1≻DMUj2≻…≻DMUjn

(11)

其中 {j1,j2,…,jn}是{1,2,…,n}的一个全排列。 我们考察使排序(11)保持不变的α的变化范围。

(11)式等价于Hj1>Hj2>…>Hjn，或

Hji-Hji+1>0,i=1,2,…,n-1

(12)

使用式(10)得：

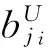
整理后有：

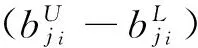
则有：

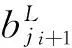
(13)

令：

(14)

则对于任意α满足0≤α<α1，排序结果(11)保持不变。

不妨设α1<1，易见当α=α1，排序(11)中至少有一个符号≻变为～；当α>α1，排序(11)将变为新的排序。

类似上面的讨论，可找到α2>α1，使新的排序在α∈(α1,α2)时保持不变，…，经有限步后，将找到某αk=1。这样可得到k个区间(0,α1)、(α1,α2)、…、(αk-1,1)，使得在每个区间中的决策单元排序保持不变，也就是说，排序结果对于乐观系数 有较强的稳定性。

4 数值例子

为了增加可比性，本文选用文献[7-8]的例子进行计算，具体数据见表1。在表1中有5个DMU，每个DMU有3种输入x1,x2,x3和2种输出y1,y2。

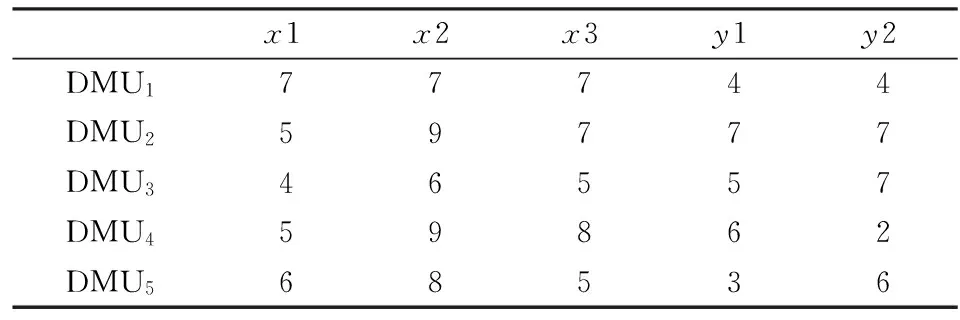
表1 各DMU的输入和输出值

求解(CCR)d模型(d=1,2,…,5)后出现以下两种情况。

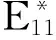
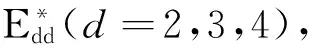
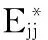
表2 各DMU的和值

由表2可得到各DMU的区间效率值，为方便比较，表3给出了本文和文献[7]的结果。对于区间效率值的上限，本文与文献[7]的取值是相同的，均为CCR模型的决策单元最大效率值。对于下限，本文在保持其他决策单元自身最大效率值不变的前提下，极小化其最优权重被所要评价的决策单元使用所得到的交叉效率值，并以这些最小交叉效率值中的最小者作为区间效率值的下限；文献[7]则以这些最小交叉效率值的平均值作为下限。可以看到，本文确定的区间效率值下限较小，而且更符合“区间效率值的下限是DMU最差的相对效率”[7]的含义。

表3 各DMU的区间效率值

下面根据区间效率值对各DMU进行排序，我们考虑乐观系数α∈[0,1]的所有情形。首先，由公式(14)可求得α1=0.46326，并得到如下结果：

当0≤α<0.46326时，DMU3≻DMU2≻DMU5≻DMU1≻DMU4；

当α=0.46326时，DMU3≻DMU2≻DMU5≻DMU1～DMU4；

当0.46326<α<1时，DMU3≻DMU2≻DMU5≻DMU4≻DMU1；

当α=1时，DMU3～DMU2≻DMU5～DMU4～DMU1。

可见，决策者风险偏好的变化会影响到区间效率值的排序结果，但其影响的稳定性可以较好地展示出来。

5 结语

从乐观角度计算点效率值的传统DEA方法只给出了区间效率值的上限，而交叉效率评价方法为计算区间效率值的下限提供了新的思路，但该评价方法由于交叉效率值的可能不唯一性而存在需要额外解多个附加辅助线性规划的缺陷。本文提出通过求传统DEA线性规划模型的多个基最优解以获得区间效率值下限的新方法，从而大大减少了计算工作量。另一方面，由于区间效率值的上限和下限分别是从乐观和悲观两个不同的角度评价决策单元的效率值，而实际上大部分决策者对风险的态度介于乐观和悲观两者之间，因此有必要引入考虑到决策者风险偏好的排序方法。本文借鉴Hurwicz决策准则，构建了决策单元区间效率值的排序方法，并论证了该方法的排序结果对乐观系数的变化有较强稳定性。本文的研究基于固定规模报酬假设下的CCR模型，由于CCR模型所求得的决策单元相对效率为总效率，并未区分技术效率和规模效率，因此，输入输出数据属于确定性数据以及需要考虑决策者风险偏好的决策单元总效率值评价问题，适用本文的研究结果。本文进一步的研究方向是变动规模报酬条件下决策单元的技术效率区间以及输入输出数据不确定情形下的决策单元区间效率问题。

[1] Charnes A, Cooper W W, Rhodes E. Measuring the efficiency of decision making units [J]. European Journal of Operational Research, 1978, 2(6): 429-444.

[2] 范建平, 陈静, 吴美琴，等. 三元效率区间下决策单元的全局绩效评价 [J]. 中国管理科学, 2016, 24(2): 153-161.

[3] 王美强, 李勇军. 具有双重角色和非期望要素的供应商评价两阶段DEA模型 [J]. 中国管理科学, 2016, 24(12): 91-97.

[4] 安庆贤, 陈晓红, 余亚飞，等. 基于DEA的两阶段系统中间产品公平设定研究 [J]. 管理科学学报, 2017, 20(1): 32-40.

[5] Azizi H, Jahed R. An improvement for efficiency interval: efficient and inefficient frontiers [J]. International Journal of Applied Operational Research, 2011, 1(1): 49-63.

[6] Wang Yingming, Yang Jianbo. Measuring the performances of decision-making units using interval efficiencies [J]. Journal of Computational and Applied Mathematics, 2007, 198(1): 253-267.

[7] 王美强, 梁樑. CCR模型中决策单元的区间效率值及其排序 [J]. 系统工程, 2008, 26(4): 109-112.

[8] 吴杰, 梁樑. 一种考虑所有权重信息的区间交叉效率排序方法 [J]. 系统工程与电子技术, 2008, 30(10): 1890-1894.

[9] 薛声家, 王清. 基于超效率模型的决策单元区间效率值排序 [J]. 暨南大学学报(自然科学与医学版), 2011, 32(5): 447-450.

[10] Doyle J, Green R. Efficiency and cross-efficiency in DEA: derivations, meanings and uses [J]. Journal of the Operational Research Society, 1994, 45(5): 567-578.

[11] Sexton T R, Silkman R H, Hogan A J. Data envelopment analysis: Critique and extensions [J]. New Directions for Program Evaluation, 1986, 32: 73-105.

[12] Doyle J R, Green R H. Cross-evaluation in DEA: Improving discrimination among DMUs [J]. INFOR formation Systems & Operational Research, 1995, 33(3): 205-222.

[13] Wu Jie, Sun Jiasen, Liang Liang. Cross efficiency evaluation method based on weight-balanced data envelopment analysis model [J]. Computers & Industrial Engineering, 2012, 63(2): 513-519.

[14] 李春好, 苏航. 基于交叉评价策略的DEA全局协调相对效率排序模型 [J]. 中国管理科学, 2013, 21(3): 137-145.

[15] 张启平, 刘业政, 姜元春. 决策单元交叉效率的自适应群评价方法 [J]. 中国管理科学, 2014, 22(11): 62-71.

[16] 薛声家, 左小德. 确定线性规划全部最优解的方法 [J]. 数学的实践与认识, 2005, 35(1): 101-105.

Ranking of Interval Efficiencies Based on New Computational Method for Cross Efficiency

CHENG Da-jian，XUE Sheng-jia

(School of Management, Jinan University, Guangzhou 510632, China)

A traditional CCR model of data envelopment analysis (DEA) is to evaluate decision-making units (DMUs) optimistically in self-appraisal method. The maximum of relative ratio of weighted sum of outputs to that of inputs is regarded as the relative efficiency of a DMU. However, since all possible ratios of weighted sum of outputs to that of inputs can be assumed as possible efficiencies, the efficiencies of DMUs can be measured within the range of an interval. On applying cross-efficiency method, interval efficiencies of DMUs can be constructed based on CCR model. A factor that possibly reduces the usefulness of original cross-efficiency evaluation method is that cross-efficiency scores may not be unique due to the presence of alternate optima in CCR model. To solve the problem, a two-phased approach is adopted in cross-efficiency evaluation. With respect to the shortcoming of need to solve many additionally auxiliary linear programming problems that is due to non-uniqueness of cross efficiency score in cross efficiency evaluation method, this paper proposes a new computational method to obtain interval efficiencies by means of finding multiple basic optimal solutions of the traditional DEA linear programming model. Thus, the amount of computational work is greatly decreased. The above is the first issue of this article. The second issue in the paper is the problem of ranking of interval efficiencies for DMUs. The maximum efficiency of a DMU in CCR model is regarded as its upper bound of interval efficiency. On the condition of keeping the maximum efficiencies of other DMUs, cross efficiencies of a rated DMU is minimized and the minimum of all minimum cross efficiencies of a rated DMU is regarded as its lower bound of efficiency interval. At the same time, because the attitude to risk of most decision-makers lies between pessimism and optimism, a ranking method for interval efficiencies of DMUs, which can consider decision-makers’ levels of optimism, is constructed by Hurwicz decision criterion, and a stability analysis of interval efficiencies ranking to optimistic coefficient is conducted in this article. Finally, a computational example is also given to illustrate the effectiveness of the method. Since CCR model under the condition of constant returns to scale can not divide overall efficiency of a DMU into technical efficiency and scale efficiency, the analysis of the paper can be applied to evaluation of overall efficiencies of DMUs when inputs and outputs are precise data and decision-makers’ risk preferences need to be taken into consideration.

data envelopment analysis (DEA); decision-making unit; cross efficiency; interval efficiency; multiple basic optimal solutions

2015-11-18；

2016-03-28

国家自然科学基金重点资助项目(71333007)；广东高校优秀青年创新人才培养计划项目(2012WYM_0021)；中央高校基本科研业务费专项资金资助项目(13JNQN007)

成达建(1978-)，男(汉族)，广东阳春人，暨南大学管理学院，讲师，博士，研究方向：管理科学与管理决策，E-mail:tcdj@jnu.edu.cn.

1003-207(2017)07-0191-06

10.16381/j.cnki.issn1003-207x.2017.07.021

C934

A