转盘轴承对数修形滚子的静态特性分析
何培瑜,洪荣晶,王华
(南京工业大学 机械与动力工程学院,南京 211816)
转盘轴承能够同时承受轴向载荷、径向载荷和倾覆力矩,且结构紧凑,中间空间大,工作时具有回转阻力小、转动灵活、安装和维护方便等优点,主要应用在起重机械(港口起重机、汽车起重机、塔式起重机)、工程机械(挖掘机)、化工机械、医疗设备、军事装备(雷达、坦克等)、风力发电设备和娱乐设施等领域[1]。
直素线滚子受载后两端会产生边缘应力集中,将使轴承的疲劳寿命大大降低[2-3],故需对滚子进行修形。工程中主要使用的滚子修形曲线有圆弧曲线、直线加圆弧、对数曲线[3-4],对数曲线被认为是最佳。对数素线修形滚子在滚子中部70%的长度上接近于直线,在两端曲率变化很快,沿长度方向接触应力均匀分布,有利于承载[4]。
文献[4]对直素线、相切圆弧素线、相交素线和对数素线进行接触应力分析;文献[5]基于ABAQUS建立不同修形滚子轴承模型,分析在有无剥落缺陷情况下的轴承振动特性;文献[6]建立圆柱滚子、对数滚子和圆弧修形滚子的三维模型,考虑了滚子形状、滚道材料、偏载的影响,不同修形滚子的极限承载能力有很大不同;文献[7]建立不同结构尺寸的修形滚子三维有限元模型,分析其接触应力和应力集中;文献[8]建立倾斜工况下的滚子与滚道接触模型,并将Hertz接触理论和有限元解对比,验证程序的准确性;文献[9-10]将Boussinesq理论和影响系数法结合起来,求解表面轮廓的接触问题,分析正载和偏载工况下的应力分布情况;文献[11]改进了Hartnett的方法,将接触区域沿接触宽度方向的单元划分为偶数,避免病态方程组;文献[12]提出在滚子修形量计算时必须考虑倒角半径和退刀槽宽度,并给出了相应的数值计算方法,该方法可以有效避免边缘效应,提高轴承寿命。
国内外学者对对数修形滚子的应力分布做了大量研究,但偏载工况下对数修形滚子接触应力的分析较少。鉴于此,分析受纯径向力工况、中心偏载工况和偏中心倾斜工况下对数修形滚子对转盘轴承应力分布的影响,以便为转盘轴承的设计提供参考。
1 对数修形滚子有限元模型
以131.32.940Z转盘轴承为例,其结构如图1所示,三排滚子转盘轴承的上排滚子尺寸为φ32×32 mm,个数为80,中间滚子尺寸为φ20×20 mm,个数为115,下排滚子尺寸为φ25×25 mm,个数为100,选择下排滚子建立局部滚子与滚道接触模型,局部滚道选取长为16 mm,宽为10 mm,高为10 mm。在滚子与滚道接触区域网格细化,远离接触区域网格较大,网格划分如图2所示。转盘轴承套圈材料为42CrMo,滚子材料为GCr15,材料参数见表1。
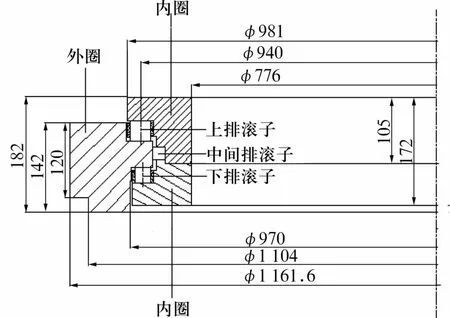
图1 结构示意图Fig.1 Diagram of structure

图2 网格划分Fig.2 Meshing
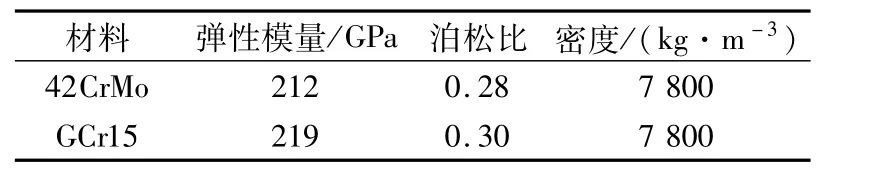
表1 材料参数Tab.1 Material parameters
对数修形滚子轮廓边缘的曲线公式为
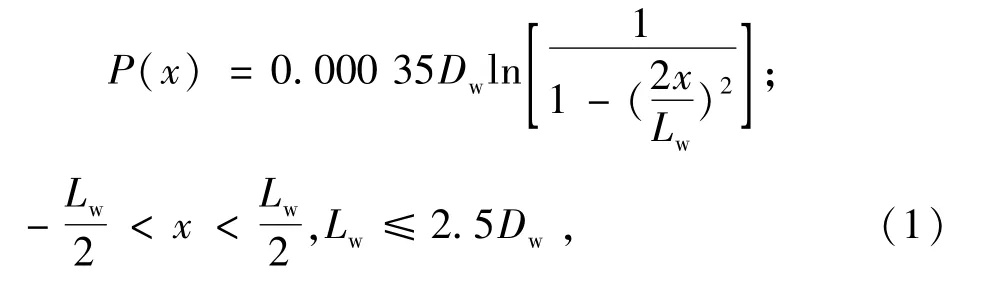
式中:Lw为滚子长度;Dw为滚子直径。
2 仿真与分析
2.1 纯径向力工况
在外圈施加纯径向力,如图3所示。滚子和内外圈建立对称约束,内圈内径面施加完全约束,滚子具有z轴平移自由度和y轴旋转自由度,外圈释放z轴平移自由度。在外滚道上施加10 kN载荷时整体模型的等效应力云图如图4所示,各零部件的最大等效应力位于接触表面下方,在滚子与滚道接触线上,从滚子中间向端部应力逐渐降低,滚子端部无应力集中。
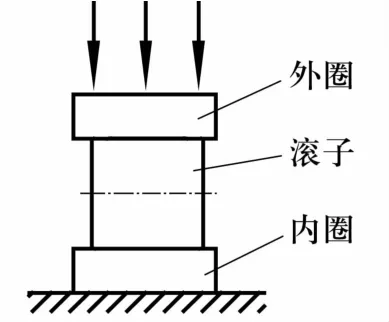
图3 加载示意图Fig.3 Diagram of loading
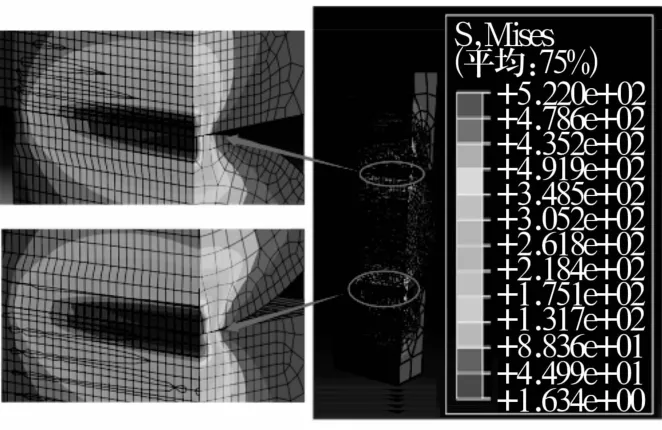
图4 加载10 kN时整体模型的等效应力云图Fig.4 Equivalent stress nephogram of whole model when load is 10 kN
滚子在外载荷分别为10,15,20,25,30 kN时的等效应力、接触应力及位移如图5—图7所示。
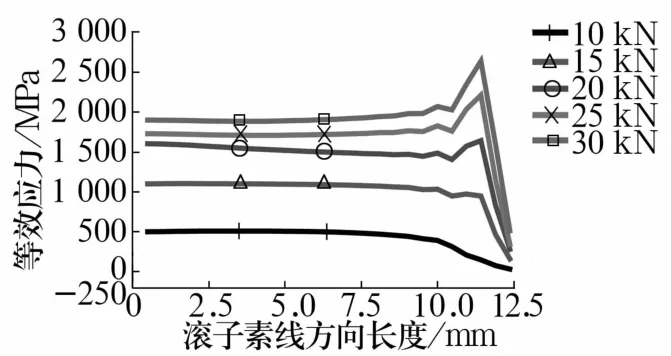
图5 不同载荷下滚子的等效应力Fig.5 Equivalent stress of roller under different loads
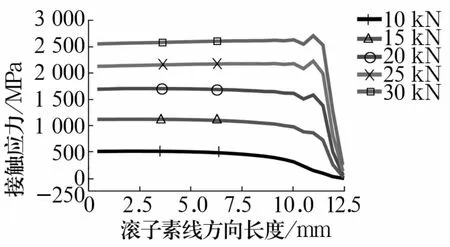
图6 不同载荷下滚子的接触应力Fig.6 Contact stress of roller under different loads
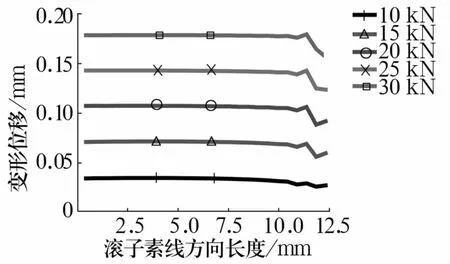
图7 不同载荷下滚子的位移Fig.7 Displacement of roller under different loads
由图可知,在载荷较小时,滚子应力变化平稳,没有突变,这表明对数修形滚子受载时整个滚子受力均匀。随载荷增大,达到20 kN时,对数修形滚子的端部有突变,加载位移越大,突变越明显。这是因为滚子与滚道的相互作用线不等长,在接触的端部区域材料变形量不同,载荷较小时滚子两端没有或少量与滚道接触,随载荷增大,滚子两端与滚道接触,在滚子端部出现应力集中。载荷过大,会使滚子端部出现严重的应力集中,造成滚子或滚道的早期疲劳破坏。
2.2 中心偏载工况
转盘轴承在实际工作时,由于内外滚道变形、径向力加载、内外圈倾斜等原因,滚子处于偏载状态,滚子会向一端倾斜,造成滚子边缘应力集中。滚子中心偏载工况下,外滚道受到向下载荷的同时,滚子中心对应的滚道倾斜一定的角度,如图8所示。

图8 滚子中心偏载工况示意图Fig.8 Diagram of center partial load condition of roller
建立1/2三维模型,滚子和内滚道建立对称约束,内滚道底面完全约束,滚子释放z轴平移自由度和y轴旋转自由度,在外滚道上方选择一点设置为参考点,外滚道与参考点RP1建立耦合关系,释放参考点RP1的z轴平移自由度和y轴旋转自由度,载荷施加在参考点RP1上。施加向下载荷10 kN,倾角为0.01 rad时整体模型的等效应力如图9所示,内滚道与滚子端部接触位置出现应力集中,这是由于外滚道有一个倾角,滚子中间处与内滚道不接触,接触主要在滚子端部。
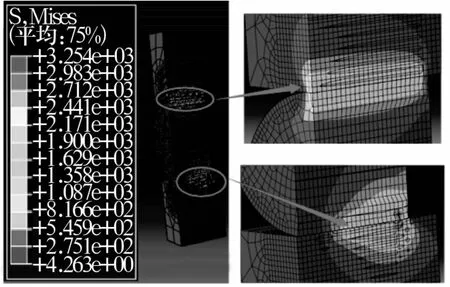
图9 倾角为0.01 rad时整体模型的等效应力Fig.9 Equivalent stress of whole model when inclination angle is 0.01 rad
施加载荷为10 kN,倾角分别为0.01,0.02,0.03,0.04,0.05 rad时,模拟中心偏载工况。不同倾角下滚子的等效应力、接触应力、位移如图10—图12所示。
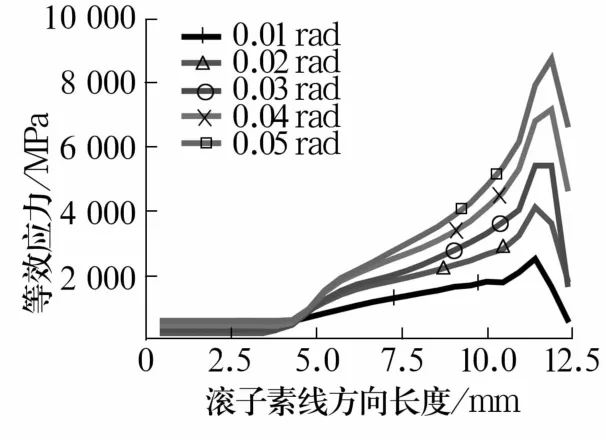
图10 不同倾角下滚子的等效应力Fig.10 Equivalent stress of roller under different inclination angles
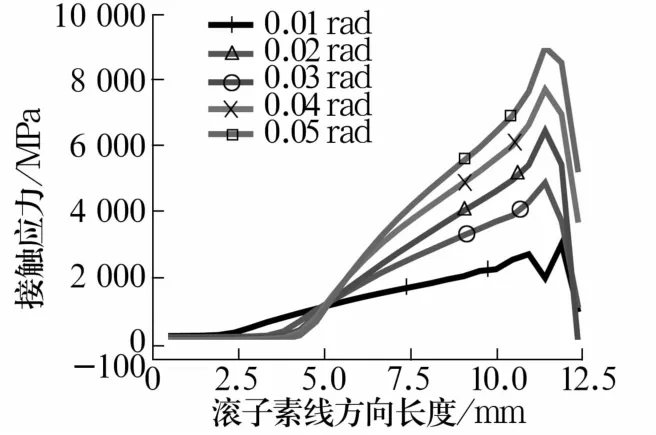
图11 不同倾角下滚子的接触应力Fig.11 Contact stress of roller under different inclination angles
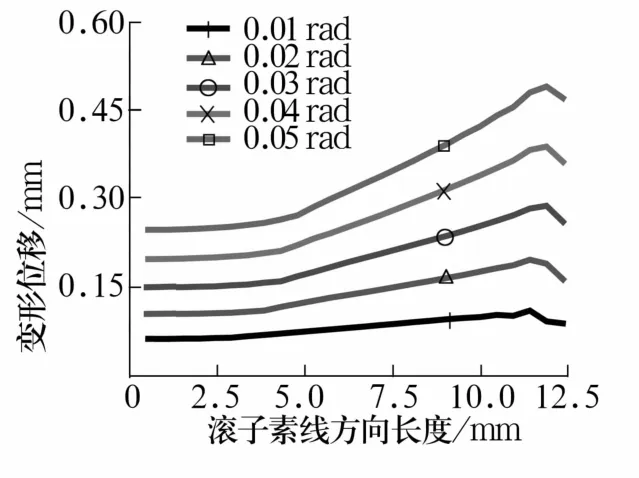
图12 不同倾角下滚子的位移Fig.12 Displacement of roller under different inclination angles
由图可知,随倾角增大,应力和应变均增大,且趋势相同,对数修形滚子端部出现明显的应力集中。滚子中间位置接触应力为负值,受拉力,从滚子接触线到滚子端部,接触应力数值变为正,开始受压力,并逐渐增大,增大到最大值后再减小,最大值在滚子端部与滚道接触位置。
2.3 偏中心倾斜工况
滚子偏中心倾斜工况是滚子受载发生倾斜时,其倾斜旋转中心不在滚子中心位置,发生偏移,如图13所示。
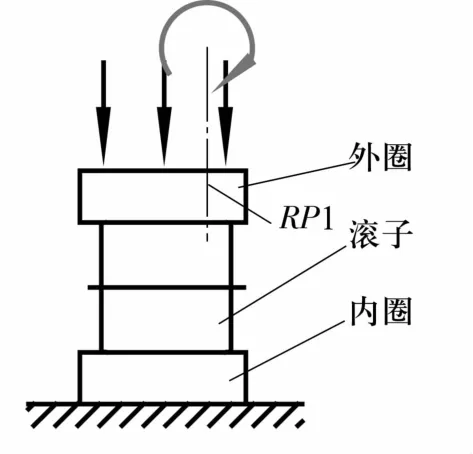
图13 滚子偏中心倾斜工况示意图Fig.13 Diagram of offset center tilt condition of roller
建立1/2三维模型,滚子和内滚道建立对称约束,内滚道底面完全约束,滚子释放z轴平移自由度和y轴旋转自由度,外滚道与参考点RP1建立耦合关系,参考点RP1偏离滚子对称中心位置,释放z轴平移自由度和y轴旋转自由度,载荷施加在参考点RP1上。施加向下载荷10 kN,倾角为0.05 rad时整体模型的等效应力如图14所示,外滚道与滚子接触面积大,内滚道在滚子端部有小面积的接触,出现应力集中,且数值较大。在实际工况中,偏载工况造成滚子偏斜,端部与滚子接触,造成应力瞬间增大,当超过材料承受的极限时,出现点蚀、剥落等故障,会加速转盘轴承的失效。

图14 倾角为0.05 rad时整体模型的等效应力Fig.14 Equivalent stress of whole model when inclination angle is 0.05 rad
施加载荷10 kN,分别施加倾角0.01,0.02,0.03,0.04,0.05 rad,模拟外滚道倾斜工况,不同倾角下滚子的等效应力、接触应力、位移分别如图15—图17所示。

图15 不同倾角下滚子的等效应力Fig.15 Equivalent stress of roller under different inclination angles
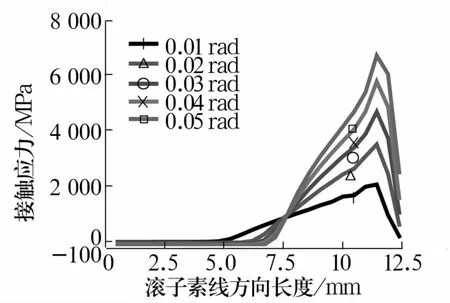
图16 不同倾角下滚子的接触应力Fig.16 Contact stress of roller under different inclination angles

图17 不同倾角下滚子的位移Fig.17 Displacement of roller under different inclination angles
由图可知,等效应力、接触应力、位移变化趋势相同,随倾角增大,滚子端部与滚道接触面积变小。相同载荷下,随接触面积变小,应力增大,应力集中更严重。与中心偏载工况相比,该工况下应力集中更严重。
3 分析与讨论
滚子失效可能发生在端部也可能发生在滚子的其他部位,滚子修形是为了尽可能使素线上的应力分布均匀,提高滚子的承载能力,避免滚子局部应力集中造成滚子提前失效。
从滚子与滚道接触线上按顺序选取应力点,然后求出应力点之间的方差,作为判断对数修形滚子素线上应力均匀分布程度的评价指标。方差为
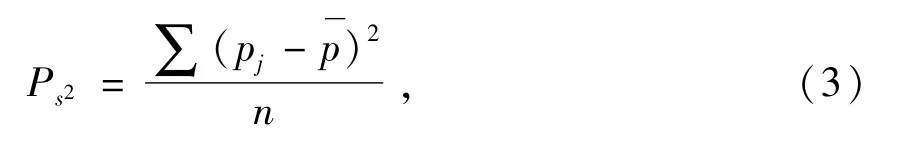
式中:Ps2为应力方差;pj为某点应力值,为所有点应力平均值;n为应力点数[13]。
滚子中心偏载工况下滚子与滚道接触线上的应力方差如图18所示,随倾角增大,等效应力和接触应力方差增大,说明倾角越大,滚子与滚道接触线上应力分布波动越大。

图18 滚子中心偏载工况下滚子与滚道接触线上的应力方差Fig.18 Stress variance on contact line of roller and raceway under center partial load condition of roller
滚子偏中心倾斜工况滚子与滚道接触线上的应力方差如图19所示,随倾角增大,等效应力和接触应力方差增大,滚子与滚道接触线上的应力分布波动越大。
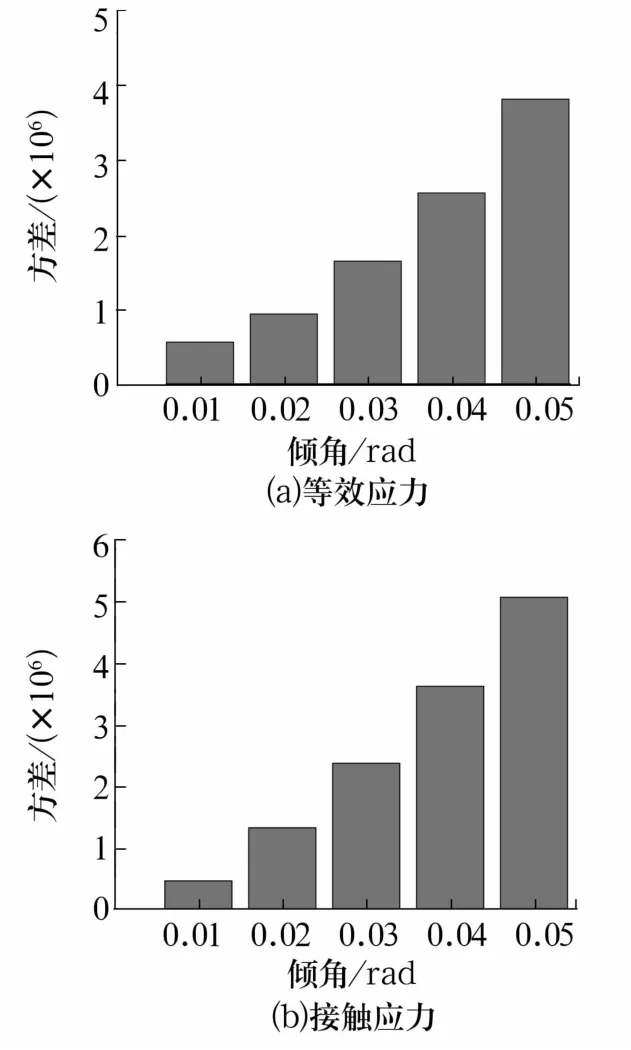
图19 滚子偏中心倾斜工况下滚子与滚道接触线上的应力方差Fig.19 Stress variance on contact line of roller and raceway under offset center tilt condition of roller
4 结束语
对转盘轴承对数修形滚子在静态工况下的纯径向力、滚子中心偏载和滚子偏中心倾斜工况应力分布进行分析,对数修形滚子轻载时,应力分布均匀,当承受重载和偏载时,滚子边缘会出现集中,且随着载荷和偏角增加,滚子应力集中越明显,各应力点之间差值越大,波动情况越剧烈。对数修形滚子应力分布与施加的载荷大小和性质有密切关系,在转盘轴承选型时要考虑修形滚子的各种工况,并对各种工况进行分析,对比其他修形滚子的应力分布情况,综合选取最优的修形滚子。

