基于假设检验法的风力发电机轴承健康系数研究

王怡祖，陆金桂，程智虎

(南京工业大学 机械与动力工程学院，南京 211816)

近年来，随着清洁能源的推广，风力发电机的装机量日益上涨，在电力能源及可再生能源中的比重越来越大[1]。风力发电机的稳定运行是风场运维的重要任务[2]，在风力发电机出现故障之前准确评价机器的健康状况，有利于风场运维部门合理安排风力发电机诊断检修，从而降低风场的运营成本。目前，主要通过数学模型和人工智能方法对风力发电机健康评价问题进行分析。文献[3]建立了齿轮箱正常运行的温度模型，通过预测温度与实际温度的残差判断齿轮箱是否存在故障隐患。文献[4]使用最大绝对误差、最大相对误差、平均相对误差、相对均方根误差等4种误差作为预测精度指标对齿轮箱故障进行预警。文献[5]运用K-S检验法比较正常与故障工况下的振动信号判断齿轮故障。

上述研究运用残差与误差等理论进行健康评价，忽视了数理统计中随机现象的统计规律性，而且没有使用评价方法对健康状况的优劣程度进行量化处理，无法从直观角度评判在役风力发电机的运行情况。另外，使用上述方法时需加装传感器，将增加风场运维成本。因此，基于风场自带的检测系统，从客观量化的角度出发，基于假设检验法对在役风力发电机轴承的数据进行健康系数的实例分析，以对风力发电机轴承的健康状态做出合理推断。

1 健康系数计算原理

当前风场都配备了数据采集与监视(Supervisory Control And Data Acquisition，SCADA)系统，可以进行现场设备的控制、参数设置、数据采集以及信号报警等[7]。由于每个风场记录的SCADA指标不尽相同，用于提取数据的风场包括92个遥测站点，分别包含压力、温度、角度、速度等方面的指标,因此分析各个部件时需对具体指标进行相应的筛选。综合比较了海装、名扬、GE等主流风力发电机品牌，在提取共有指标参数的基础上，结合叶片经叶轮通过主轴及轴承传入齿轮箱的原理，对于轴承的健康评估选取了与温度和转速相关的指标量，主要包括风速、主轴转速、主轴温度和齿轮箱轴承温度。

由于上述指标之间存在耦合性，因此选用神经网络模型将风速、主轴转速、主轴温度作为输入，将轴承温度作为输出，利用正常工况下的指标作为神经网络的训练数据。同时，在健康评估过程中利用在役数据进行预估，得出轴承温度的神经网络预估值，利用假设检验方法将其与监测系统中的实际温度进行对比计算，求出轴承的健康系数值。若轴承温度的预估值与实际值存在明显差异，则说明轴承出现故障；若不存在问题，则通过健康系数值说明其运行状态的优劣。

由于轴承温度的预估值与实际值的分布是杂乱无章的，不符合任何分布形式，因此需要通过数理统计方法进行近似变幻。在独立同分布的Lindeberg-Levy中心极限定理中，设X1，X2，…，Xn是相互独立且服从同一分布的随机变量序列[6]，其数学期望和方差为

EXi=μ,DXi=σ2≠0；i=1,2,…，n，

则对任意的x有

无论随机变量服从什么分布，只要满足定理的条件，即随机变量序列

当n无限增大时，总以标准正态分布为其极限分布，或者说当n充分大时，Yn近似服从标准正态分布。利用这一理论，在数理统计中许多复杂随机变量的分布都可以用正态分布近似。

通过上述理论将轴承温度的预估值与实际值近似为正态分布，然后运用正态分布下的假设检验法进行健康系数的分析。

实际应用中，常遇到两正态总体参数样本的比较问题，如2台机床加工零件的精度是否有差异等，一般可归纳为两正态总体参数的假设检验。

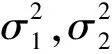
故对于给定的显著性水平α，检查正态分布表得临界值Zα/2,再由样本的具体观察值计算得统计量Z的观察值为

将Z与Zα/2比较，若|Z|≥Zα/2，则拒绝H0，反之接受。

根据上述计算步骤，在标准正态分布表中，统计量Z所代表的数值唯一对应了其中一个概率，此概率值说明了两者近似程度的大小，因此通过概率值的大小可代表健康系数的大小。正常状态下，预测值与实际值差异不大，健康系数较高，可判定为正常。非正常情况下，若数据极端超过阈值，则会出现停机报警；若数据异常不明显，不超过阈值，无法通过阈值报警，即不会出现急停，但经过健康系数分析，虽然无明显停机症状，健康值较低时仍需及时维修。

2 健康系数计算方法

如图1所示，对于轴承的健康评价主要根据检测量判定，并根据严重程度对风力发电机组做出诊断。若监测值超过风机正常运行所设定的阈值，则发出故障报警，需停机维修；若未超过阈值，则通过神经网络进行判断。

图1 健康评价模型

根据经验公式m=2n+1(m为隐含层节点数，n为输入层节点数)，选用1个隐含层，隐含层节点数选为7，建立如图2所示的神经网络结构模型。参数选择过程中，基于在役数据的时效性，学习速率设置为0.5，误差精度为0.001，最大迭代次数为3 000。隐含层传递函数选用Log-Sigmoid,输出层传递函数选用线性函数，学习函数选用Levenberg-Marquardt函数。神经网络结构模型建立后，利用正常运行下的监测数据建立神经网络评估模型，基于在役运行时段下的监测数据获得轴承温度的神经网络预估值。然后运用假设检验方法比较轴承温度的预估值与实际值之间的差异，计算出健康系数值，得出一个量化的优劣值，从而对风电轴承的健康状态做出合理、科学的推断。

图2 神经网络预估模型

3 实例分析

选取2013年10月—2014年9月新疆某风场1.5 MW风电机组平稳运行状态下的SCADA系统19 686组监测数据(表1)进行神经网络的训练，建立神经网络评估模型。

表1 神经网络学习数据

3.1 正常风机的系数判断

选择同机组2015年1月份正常运行的801组监测数据(风速、主轴转速及温度)作为神经网络的输入量，使用训练好的神经网络进行轴承温度预估，结果见表2。

表2 神经网络预估数据(正常)

获得上述数据后，使用如下步骤从量化的角度运用健康系数值对轴承的健康状况进行评价：

表3 服从正态分布

2)做出原假设H0，即预测值与实际值不存在明显差异。

5)判断。因2.288介于2.28与2.29之间，因此，当α=0.022时，|Z|=2.288<2.29，接受原假设H0。当α=0.022时，在正态分布表中对应的概率值为0.989，即有98.9%的可靠度认为预测值与实际值不存在显著差异。

由上述步骤可得，该轴承健康系数为98.9，健康状况等级良好，与传感器信号系统分析结果一致(健康系数值约95)，无需进行维修处理。

3.2 故障风机的系数判断

选择同机组2015年5月份异常运行的801组监测数据作为神经网络的输入量，使用训练好的神经网络进行轴承温度预估，结果见表4。

表4 神经网络预估数据(异常)

同理，经计算得|Z|=0.267，则

因为0.267介于0.26与0.27之间，所以由上述结果可知当α=0.787 2时，|z|=0.267<0.27，接受原假设H0，即只有有60.64%的可靠度认为预测值与实际值不存在显著差异。

由此可知，该分析所使用的风机轴承健康系数为60.64，健康状况等级较差，与传感器信号系统分析结果一致(健康系数值约55)，需要进行维修处理。

4 结束语

在数理统计的范畴之内，考虑了概率对健康评价的影响，运用假设检验方法及数理统计计算模型，对神经网络试验数据的实际值与预测值进行对比分析，计算出了基于概率的健康系数值，从而对在役风力发电机轴承的健康状态做出合理的、科学的评价。同时，通过对在役风电机组轴承的SCADA数据进行健康系数的实例分析，验证了该方法的有效性。

从计算过程可知，预测值与实际值之间仍存在一些差异，但通过数理统计的方法进行数据处理在实际中是可行的，后续需要对健康系数值大小与健康状况等级的对应方面进行更深入的研究。