基于MED-EMD和切片双谱的滚动轴承故障特征提取

李延峰，韩振南，刘邱祖，王志坚

(1.太原理工大学 机械工程学院，太原 030024；2.中北大学 机械与动力工程学院，太原 030051)

轴承是风力发电机齿轮箱中的关键零件，是齿轮箱正常、高效运行的保障。轴承的振动信号通常表现为调频、调幅形式，各成分之间相互叠加，信号具有非线性、非平稳、非高斯和复杂性等特点[1]，传统的频谱分析方法将信号假定为平稳高斯信号进行处理，会出现严重的“频率模糊”现象[2]。经验模态分解(Empirical Mode Decomposition，EMD)[3-5]能将复杂的多分量信号分解为有限个本征模态函数(Intrinsic Mode Function，IMF)之和，每个IMF分量所包含的频率成分不仅与分析频率有关，而且具有自适应的特点，具有很高的信噪比，非常适合处理非线性和非平稳信号[5]。但强背景噪声下EMD的分解效果不佳，易出现模态混叠[3]现象，需要对信号进行预处理。

最小熵解卷积(Minimum Entropy Deconvolution，MED)非常适用于冲击性故障的降噪处理，突出冲击脉冲[6]。另外，传统的基于EMD的故障诊断方法大多采用包络的功率谱分析技术，其不能够抑制高斯噪声对EMD的影响，极大限制了EMD在工程中的使用[4]。因此，采用高阶谱分析技术[7-8]以抑制高斯噪声的影响，提高分析和辨识精度,同时更容易获得相位信息。

综上所述，尝试将MED，EMD和切片双谱相结合，采用MED对信号初步降噪，增大故障信号特征，再用EMD将含背景噪声的故障信号分解为含有不同频率特征的各阶IMF分量，选择与原始信号相关性强的IMF分量并计算其切片双谱，去除高斯噪声，从而获得包含较多故障信息的特征频率。

1 故障诊断机理

当旋转机械发生故障时，采样信号的特征为受干扰的冲击调制信号[9]，即

n(t)，

(1)

式中：ωi为调制源；ω0为载波频率;b为任意常数；n(t)为噪声。

轴承故障冲击为微弱特征信号，由MED的原理可知，通过解反褶积可以突出尖脉冲，因此可采用MED对轴承故障信号进行降噪处理。设当滚动轴承发生故障时采集到的离散信号为

y(n)=h(n)*x(n)+e(n)，

(2)

式中：h(n)为传递函数；x(n)为滚动轴承的冲击序列；e(n)为环境噪声。x(n)受环境和传递路径的影响而失去了原本的物理特性，而解卷积的目的就是得到逆传递函数f(n)，再由输出y(n)恢复冲击序列x(n)，即

x(n)=f(n)*y(n)，

(3)

当f(n)的估计值最优时，x(n)熵变最小，冲击性最强。

MED处理后，故障信号依然混杂在复合信号中无法识别，将信号y(t)进行EMD处理得[4]

(4)

式中：ci(t)为第i个IMF分量；rn(t)为趋势分量。

对各IMF分量进行分析可识别微弱故障特征。对低频分量分析能够使微弱故障显而易见，而高频分量中包含故障信号的倍频，对其分析能够强化对故障信号和易混淆信号的分辨。在机械故障诊断中，故障信号通常是非高斯的，非故障信号则是高斯的[10]，切片双谱分析可以抑制高斯噪声对EMD的影响。对于零均值信号，其3阶累积量为

c3x(τ1,τ2)=E[y(t)y(t+τ1)y(t+τ2)〗，

(5)

其双谱为

exp[-j(ω1τ1+ω2τ2)〗，

(6)

记ω1=ω2=ω，则切片双谱的估计为

S3x(ω1,ω2)=S3x(ω)。

对于零均值的高斯过程，其切片双谱值为零[12]，从而抑制高斯噪声，而在旋转机械的故障特征频率点上，切片双谱则会出现明显的峰值，从而为故障识别提供了依据。

根据以上分析，将MED，EMD和切片双谱分析引入风电齿轮箱的故障诊断方法之中，诊断机理的具体流程如图1所示。

图1 复合故障特征提取流程图

2 仿真分析

为验证MED-EMD切片双谱方法的可行性，设置仿真信号为

x(t)=[1+cos(2πfr1t)+cos(2πfr2t)〗·

cos(2πfnt)+n(t)，

(7)

式中：n(t)为均匀分布随机噪声；采样频率fs=1 200 Hz，采样点数为1 000；调制频率fr1=70 Hz，fr2=200 Hz；载波频率fn=300 Hz。

如图2所示，仿真信号经过MED滤波后幅值明显增加。选取仿真信号经MED-EMD处理后的各阶IMF分量中相关性较大，即包含原信号主要成分的前3阶IMF分量为有效分量，如图3所示。虽然MED不能直接提取微弱特征频率信号，但利用其降噪能力，EMD能有效识别微弱特征成分。

图2 仿真信号及MED滤波后的信号

图3 经MED-EMD处理得到的前3阶IMF分量

对前3阶IMF分量分别进行双谱对角切片分析，如图4所示。在图4a中低频段出现了载波频率fr1，明显突出了调制频率fr2及其边频簇、fr2的2倍频及其边频簇和载波频率fn的边频簇；图4b中明显突出了调制频率fr1，fr2及其边频和载波频率fn；图4c突出了调制频率fr2的半倍频。由此可见，MED-EMD切片双谱的降噪效果较好，该算法流程可行。

3 实例分析

采集国内某大型风电公司的风力发电机实时故障信号进行实例验证，增速箱为2级传动，采集点位于中间轴齿轮箱轴承座，采样点数1000，采样频率5 333 Hz，中间轴转速为491.4 r/min，转频为8.19 Hz(调制频率)，中间轴轴承位置与轴承故障频率见表1。

图4 前3阶IMF分量的切片双谱

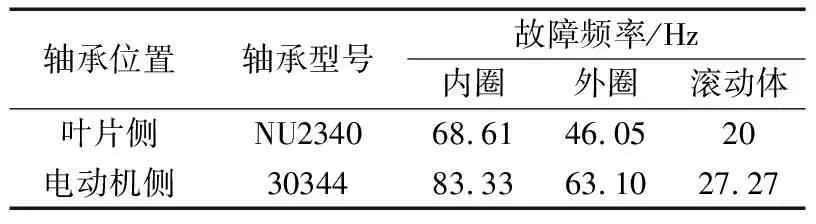
表1 轴承故障频率

对采集到的振动信号进行MED降噪处理，结果如图5所示。从图中可以看出，幅值由10 m/s2增加至15 m/s2，冲击特征更为凸显。

原始振动信号分别经EMD和MED-EMD处理后的前4阶IMF分量如图6所示。对比发现：EMD方法的模态混叠现象和端点效应比较严重， MED-EMD 的降噪效果相对较好。

对图6a中的IMF分量进行功率谱分析，结果如图7所示。第4个IMF分量中突出了轴承内圈的故障频率83.3 Hz，但却存在其他干扰成分；前3个IMF分量中则存在多种成分，故障频率淹没在噪声中，只能突出83.3 Hz的倍频，很难判断各成分频率之间的关系，总体效果欠佳。

图5 风电齿轮箱轴承振动信号

对图6b中的IMF分量进行切片双谱分析，结果如图8所示。在图8a中出现了中间轴的转动频率8.19 Hz和电动机侧轴承内圈的故障频率83.3 Hz及其2～7倍频，规律明显且完全抑制了高斯噪声，分析效果较好；图8b中则出现了83.3 Hz的2～6倍频，图8c中出现了83.3 Hz及其2倍频、5倍频和6倍频；图8d中也明显出现了83.3 Hz的2倍频；综合判断可知，很可能是中间轴靠电动机侧的轴承内圈出现了故障。进行齿轮箱检修发现，中间轴靠电机侧的轴承内圈出现了点蚀，证实了诊断结果。

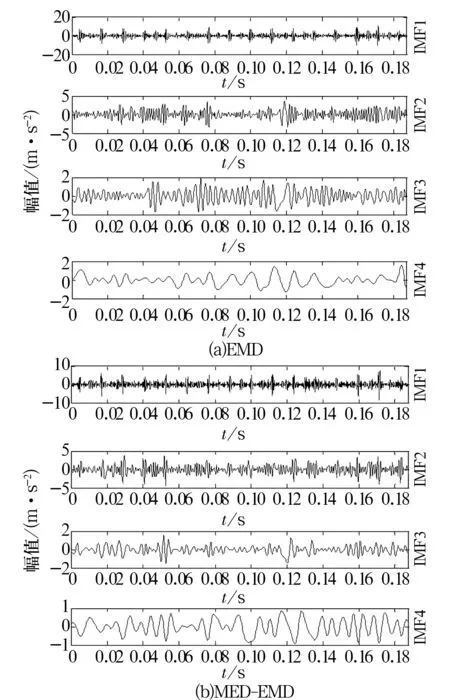
图6 原始振动信号分别经EMD和MED-EMD处理后的前4阶IMF分量

图7 经EMD处理后IMF分量的功率谱分析结果

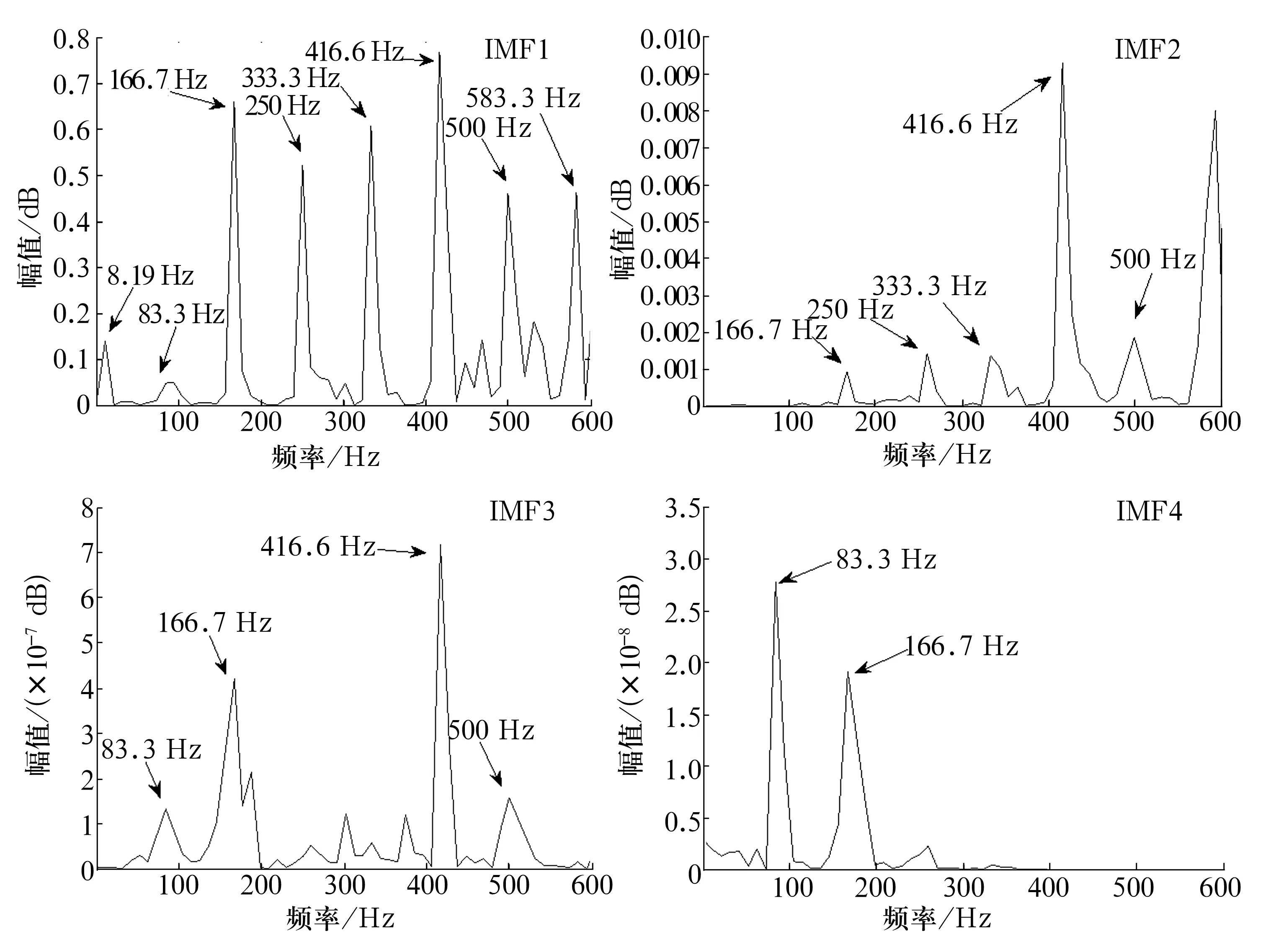
图8 经MED-EMD处理后IMF分量的切片双谱分析结果

综上所述，由于轴承振动信号的故障特征较微弱，容易被噪声干扰，且在工况复杂情况下易与其他振动成分混淆，与传统的功率谱分析相比，MED-EMD降噪与切片双谱分析的结合可成功抑制噪声并提取微弱故障特征频率，且易于判断各频率之间的关系，具有一定的优越性。

4 结束语

提出了基于MED-EMD的切片双谱分析方法，成功提取了风电齿轮箱轴承的微弱故障特征。通过仿真信号和风电齿轮箱实测信号验证了此方法的可行性，与基于EMD分解的功率谱分析方法的对比证明了此方法的优越性，对风电齿轮箱的故障诊断提供了参考。

但研究中仍有不足之处，如求各IMF分量互信息相关性时的计算量较大，对应用于故障实时监测产生了一定的限制；没有完全解决EMD分解产生的端点效应，这会影响对低频分量的分析等。这些不足成为后续研究中需要突破的瓶颈，同时，对MED方法和切片双谱的优化也会是以后的研究方向。