球面螺旋槽动静压气体轴承运动状态仿真分析

贾晨辉，王振清，邱明

(河南科技大学 机电工程学院，河南 洛阳 471003)

随着高速、超高速技术的迅猛发展，气体轴承以其独特的优点在高速旋转机械中得到愈来愈广泛的应用[1-2]。气体轴承从供气方式上可分为静压气体轴承、动压气体轴承和动静压气体轴承3类。静压气体轴承在转子启停阶段将外部的高压气体经节流器导入轴承间隙中，形成静压承载，但此类轴承在节流器处容易形成气锤现象，且轴承的加工精度高。动压气体轴承只利用轴承的动压效应所形成的动压承载能力进行承载，其缺点是在转子的启停阶段存在固体接触，干摩擦严重。动静压气体轴承综合了这两类轴承的优点，在启停阶段采用静压轴承的供气方式避免轴承间的固体接触，在高速旋转时停止外界供气，利用动压效应进行承载，大大减小了功耗[3-6]。

由于动静压气体轴承最高转速可达每分钟几十万转，轴承气膜特性的变化呈复杂的非线性随机过程[7]，直接影响转子的运动状态，因此对轴承气膜的研究是研究轴承稳定性的关键。现阶段对动静压气体轴承动态特性的分析大多是以Reynolds润滑方程为基础，通过求解线性方程组从而得到气膜的压力分布；但此方法对动静压耦合效应和气旋现象的分析误差较大[8-10]，且无法将轴承的刚度、阻尼参数与轴承稳定性进行关联，因此实用性较低。

现采用Fluent软件中6 DOF被动型网格，以球面螺旋槽动静压气体轴承的间隙气膜为研究对象，对轴承在动态运转条件下的失稳过程进行模拟分析，研究轴承从稳定运转到失稳的各种状态，确定轴承失稳时的临界转速。

1 模型的建立

1.1 球面螺旋槽动静压气体轴承的结构与润滑机理

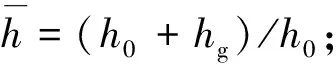
图1 球面螺旋槽动静压气体轴承剖面示意图

在轴承启动阶段，将外部的高压气体从供气孔处导入轴承间隙中，从而形成静压承载。在轴承转子相对于定子高速旋转的过程中，轴承的静压效应不断减小，轴承间隙内的黏性气体被带入轴承自身形成的楔形间隙中，随着间隙不断减小，承载压力不断增大，从而产生动压效应，形成动压悬浮[13]。

1.2 球面螺旋槽动静压气体轴承气膜模型的建立

利用空间球坐标系确定轴承螺旋线方程[14]

(1)

式中：R为半径；θ为维度角；φ为径向角。

采用Pro/E软件建立球面螺旋槽动静压气体轴承的三维气膜模型，如图2所示。将Pro/E中默认精度改为1μm，以此来满足模型精度高的要求。

图2 球面螺旋槽动静压气体轴承三维气膜模型

1.3 模型假设与边界条件确定

1.3.1 网格模型的建立

采用ANSYS软件中的CFD模块，对轴承的气膜模型进行网格划分，如图3所示。在CFD模块中，网格可以分为结构网格和非结构网格2种，由于气膜厚度只有20 μm，气膜厚度方向尺寸远远小于其他方向的尺寸，且尺寸紧密，导致网格元素纵横较大。因此采用结构网格[15]，以提高计算的精度和速度，缩短计算时间，避免网格出现负体积。网格划分过程中，网格数量越多，计算精度越高，计算时间也越长；反之，则无法满足计算要求：经反复比较，确定网格数为5×105。为了满足计算精度的要求，供气孔采用O型网格划分法，在供气孔、螺旋槽的槽肩和槽宽处网格适当加密。

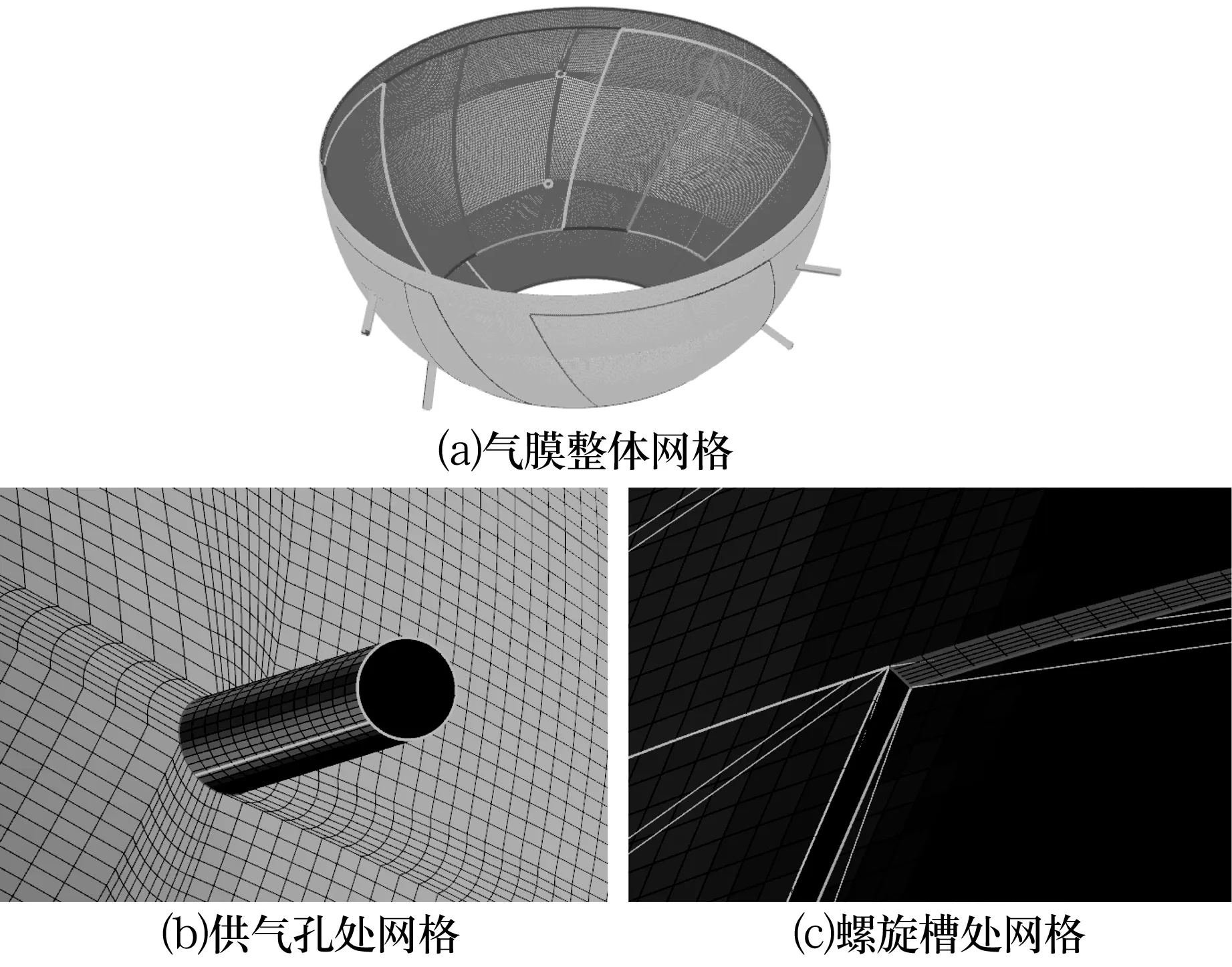
图3 网格划分

1.3.2 模型假设

球面螺旋槽动静压气体轴承的润滑分析有限元模型主要反映轴承间隙内气膜压力的分布规律，为了求解计算，作如下假设：1)润滑介质为Newton流体， 气体黏性系数为常数；2)气体与壁面之间无热量交换，且在旋转过程中不考虑轴瓦与轴颈的热变形；3)在垂直于气膜厚度的方向上忽略其压力变化，即沿膜厚方向无压力变化；4)气体在轴及轴承表面不存在相对滑动；5)轴承的壁面为光滑壁面，不考虑壁面粗糙度及滑移边界对轴承的影响。

1.3.3 边界条件的确定

在对球面螺旋槽动静压气体轴承进行分析计算时的边界条件有：1) 轴承大端为进气口，小端为出气口，且进、出气口压力与外界大气压力相等，即p0=1.013×105Pa；2)供气孔上端为压力进口，且给定供气压力p1=0.2 MPa，气体黏度μ=1.833×10-5Pa·s，空气密度ρa=1.201 kg/m3；3)其他边界部分为壁面，且各壁面间没有热交换，气体与壁面之间无相对滑动，其中内壁面设置为旋转的刚性壁面，外壁面及供气孔壁面设置为固定壁面。

2 Fluent求解与结果分析

2.1 计算求解

应用Fluent软件进行动态分析，计算流程如图4所示。

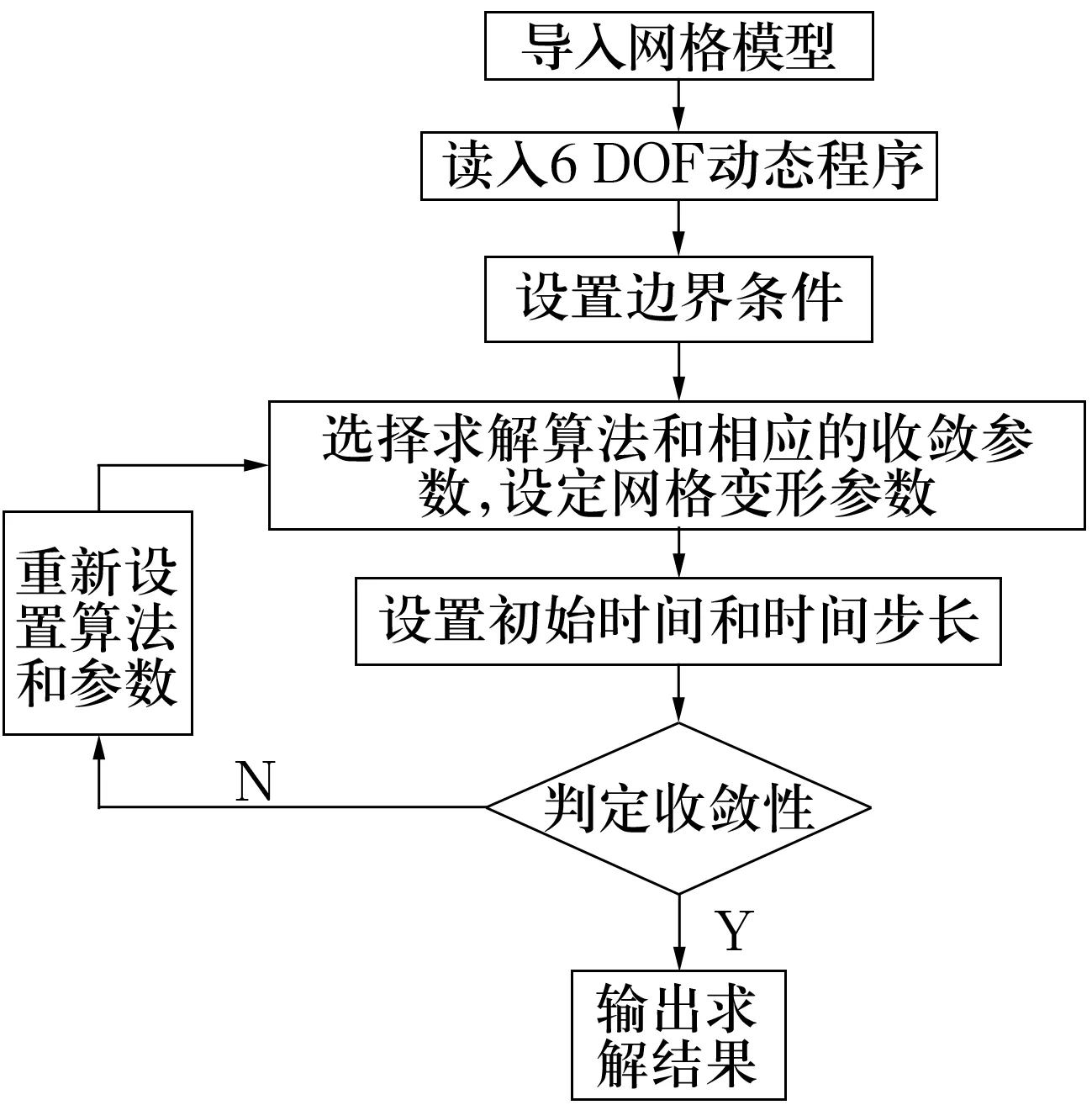
图4 计算流程图

首先进行6 DOF(6个自由度，即在空间3个方向上的转动自由度和移动自由度)动态程序编写，这是为了在Fluent计算时释放所需要的自由度。应用MATLAB软件对此程序进行编写，释放相应的自由度。由于试验中采用的是对峙半球，抵消了轴向的移动及转动自由度，故完全限制轴承的轴向自由度，释放径向移动和转动自由度，假设转子所受重力(径向力)为0.2 N，径向转动惯量为2.018×10-3kg/m2。设置模型的边界条件，同时将进气口和出气口设置为变形面，内壁面设置为运动刚体面。

计算采用Realiziblek-ε湍流模型，其能较好地模拟出供气孔旋转机械中的气旋现象。采用适合计算速度与压力耦合的SIMPLE算法，方程的离散采用2阶迎风格式，收敛参数设置为0.4。由于单位时间步长内，网格的变形量不能超过网格自身长度的一半，故将时间步长设置为0.000 01 s。

2.2 计算结果分析

2.2.1 计算数据处理

计算完成后，检测到的轴承转子运动为TXT格式文件，包含转子在x，y方向上的位置数据，将此数据导入到origin软件中，拟合出轴承的轴心轨迹图。应用MATLAB软件进行编程，通过Fourier变化，将数据转换成轴承的频谱图，从而分析轴承的运动状态。

2.2.2 轨迹图与频谱图分析

在不同转速下，轴承轴心的轨迹图和频谱图如图5—图10所示。

由图5—图10可知，随着转速的增加，轴承振幅呈先减小后增大趋势，轴心轨迹逐渐变得混乱，且出现涡动，说明轴承的稳定性逐渐变差。当转速小于30 000 r/min时，轴承只以工频稳定运转，轴心轨迹为规律的椭圆形；当转速达到40 000 r/min时，轴承频谱图中出现比较微弱的半频和2倍频，此时轴心轨迹上还没有出现明显的涡动迹象，轴承运动轨迹相对比较稳定；当转速增大到45 000 r/min时，半频频率明显增强，轴心轨迹开始出现明显的涡动；转速增大到55 000 r/min时，轴承的振动频率比较混乱，出现多种工频以外的振动频率，轨迹无规律，此时轴承处于失稳状态。

图5 10 000 r/min时轨迹图与频谱图

图6 20 000 r/min时轨迹图与频谱图

图7 30 000 r/min时轨迹图与频谱图

图9 45 000 r/min时轨迹图与频谱图

图10 55 000 r/min时轨迹图与频谱图

3 结论

随着转速的增加，轴承振动幅度呈先增大后减小的趋势，刚度和阻尼也随之变化。当转速达45 000 r/min时，轴承出现工频以外的2倍频涡动；当转速达55 000 r/min时，轴承出现多种频率的涡动，处于失稳状态。

此仿真方法能很好地模拟并区分出轴承从稳定运转到失稳过程中的各种运动状态，为研究螺旋槽动静压气体轴承的稳定性提供新的思路和研究依据。