改进的各向异性扩散图像去噪算法
肖 丹,黄玉清
(西南科技大学信息工程学院,四川 绵阳 621010)
改进的各向异性扩散图像去噪算法
肖 丹,黄玉清
(西南科技大学信息工程学院,四川 绵阳 621010)
图像去噪是图像处理中的重要环节,经典的图像去噪算法,如中值滤波、高斯滤波和加权平均滤波等,去噪效果都不是很理想。传统方法在去除噪声的同时,会使图像的边缘也变得模糊。偏微分方程(PDE)是近年比较流行的图像处理方法,它具有各向异性的特点,在去除噪声的同时,能很好地保持图像的边缘。基于现有算法,提出了一种改进的去噪算法。将传统P-M算子中的固定边缘阈值改为随梯度模变化的自适应阈值,并结合图像结构张量构造一个扩散函数。在图像平坦区,改进的P-M模型具有各向同性的特点,有利于平滑噪声;而在图像边缘处,该模型只沿切线方向扩散,有利于保护图像细节。试验表明,改进的P-M模型能很好地改善图像去噪效果,同时也能很好地保持图像的边缘。
图像去噪; 偏微分方程(PDE); 各向异性; P-M模型; 边缘阈值; 结构张量; 扩散函数
0 引言
图像去噪是图像处理的重要环节。传统的去噪方法有很多,如中值滤波、高斯滤波和加权平均滤波等[1]。这些传统的滤波方法主要是去除图像的高频成分,而图像的边缘也属于高频区域,所以对图像噪声滤除时会使图像的细节变得模糊。近年来,偏微分方程(partial differential equation,PDE)在图像去噪领域得到了广泛的应用。该方法通过扩散系数的作用,使模型自动在图像边缘处和其他平坦区产生不同的平滑作用,因此能够在去除噪声的同时,很好地保留图像的边缘。
偏微分方程中,波动方程、热传导方程和拉普拉斯方程最早使用在数学和物理学中[2]。热传导方程在1990年被Perona和Malik推广到非线性领域,建立了P-M模型[3]。该模型是基于热扩散方程的各向异性扩散模型,它对非线性扩散方程的数值方法和理论研究起到了积极的推动作用,但试验研究表明,P-M模型也存在缺陷,具有一定的局限性[4-5]。对于图像细节特征比较复杂的图像,P-M模型在去除噪声时,图像会出现“分块状”,因此有许多学者对P-M模型进行了改进。为了更好地区分图像的边缘区域,有的学者引入了结构张量[6-7]用于分析图像局部结构,提出了基于结构张量的异性扩散系数[8]。除此之外,有的学者对P-M模型中的边缘阈值进行修改。这些改进虽然都取得了较好的效果,但仍然存在一些问题。
本文通过分析P-M扩散系数,对其进行改进,并引用结构张量作为扩散系数的自变量。同时引入随梯度模变化的边缘阈值;在P-M各向异性扩散的基础上,使其再自适应地选取扩散系数。试验结果表明,在同样的测试条件下,改进后的方法所得到的峰值性噪比(peak signal to noise ratio,PSNR)更高,且对应的均方根误差(root-mean-square error,RMSE)更小,同时所需要的迭代次数也更少。
1 P-M模型的扩散函数
1990年,Perona和Malik提出了保护边缘的非线性各向异性扩散方程(P-M扩散方程):
(1)
式中:u0(x,y)为原始图像;|u|为梯度模,|u|用来区分该区域是平坦区域还是边缘区域,在平坦区,|u|的值比较小,而在边缘区,值比较大;f(|u|)为扩散系数函数,它的值表示扩散的强度,需要满足的条件是f(0)=1,limx→∞f(x)=0,且f(|u|)∈(0,1)。
基于以上条件,提出了如下两个扩散系数函数:
f1(|u|)=
(2)
f2(|u|)=exp-
(3)
2 改进的P-M模型图像去噪
P-M模型虽然能够兼顾噪声的消除和保留边缘,但也存在一定的问题:①当处理噪声图像时,噪声点的梯度较大、扩散系数较小,不能完全消除噪声,带噪声的边缘也会被破坏;②模型本身在数学上是病态的,不能保证解的存在性和唯一性[2]。这些问题会使得处理后的图像出现“阶梯”效应[11-12]。因此本文对P-M模型的扩散系数进行了改进。
通过坐标变换,可将P-M模型改写成以下的形式:
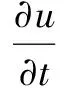
f(|u|)uζζ
(4)
式中:uηη和uζζ为u在η和ζ方向上的二阶导数。
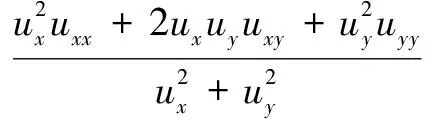
(5)
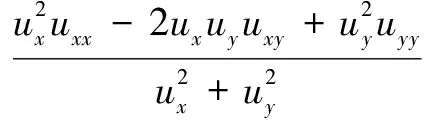
(6)
式中:ux和uy分别为u在x和y方向上的偏导数。
为解决P-M模型解的不适定性,将P-M模型改写为:
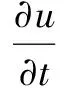
(7)
对于扩散函数f(x),要求在平坦区,f(x)趋于0.5,切线方向和梯度方向具有同等扩散;而在边缘区域,f(x)趋于0,只沿着切线方向扩散,因此采用了以下扩散函数[13]:
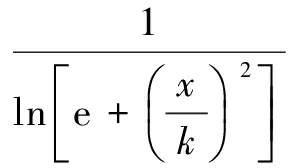
(8)
由于图像的梯度不能很好地获得图像的局部信息[14],而结构张量能获得更丰富的信息,所以引入结构张量[6-7]作为扩散函数的自变量,结构张量一般是由海森矩阵所得到的,即:
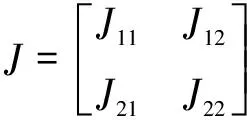
(9)
而J的两个特征值分别为:

(10)

(11)
得到结构张量|I1-I2|,从而将此代入到引用的扩散函数中。
由于扩散函数中k为固定的阈值,但当图像中噪声幅度比较大时,噪声也会产生较大的梯度值,将无法区分边缘和噪声,会使滤波性能降低,所以将阈值k改为随着梯度|u|变换的函数[15],即:
k(|u|)=kmexp[∂/1+|u|]
(12)
式中:km为迭代稳定时的边缘阈值,km=3;∂为常量。
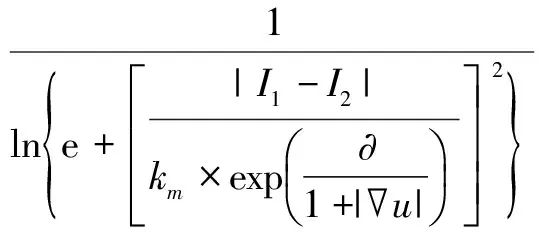
(13)
3 试验结果及分析
为了验证本文改进方法的有效性,本文选取了Pepper图像和House图像作为测试图像,分别对均值滤波、高斯滤波、维纳滤波、热扩散、P-M模型和本文改进的P-M模型进行比较,对测试图像分别加入标准差δ为30和20的噪声。
比较几种方法的去噪效果可知,本文的方法比其他方法的效果要好,本文方法在抑制噪声的同时也很好地保留了图像的细节。
表1是在不同方法下对两种性能指标测试的试验数据。根据表1可以看出,采用本文方法降低了RMSE值,提高了PSNR值。当噪声越大时,该方法的效果更佳,并且改进后算法的运行时间比传统方法的运行时间更少。
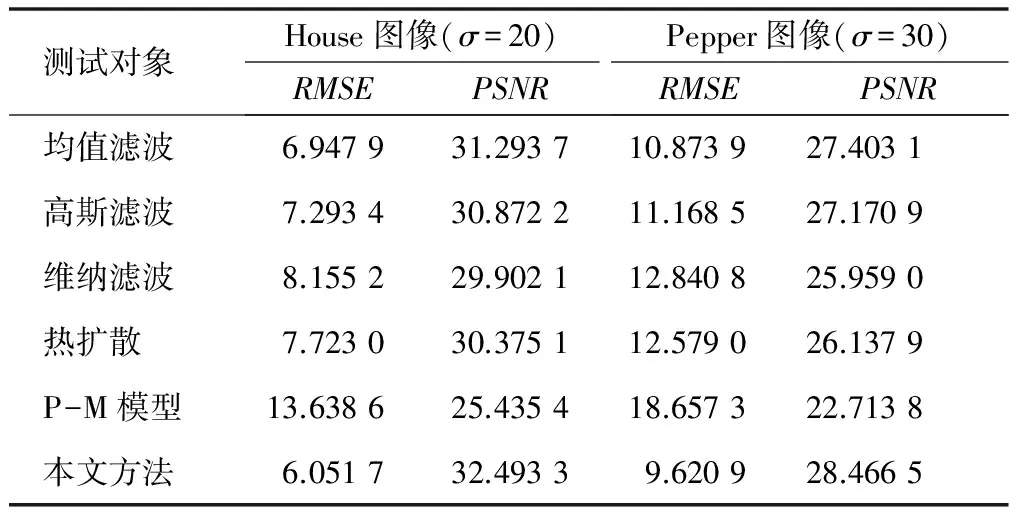
表1 试验数据
表2是后三种方法对达到相同的精确度所需要的迭代次数。由表2可以看出,本文方法所需要的迭代次数比P-M模型和热扩散所需要的次数少很多。

表2 迭代次数比较
4 结束语
本文在P-M模型的基础上,将P-M模型中的边缘固定阈值改为随着梯度模变化的函数,并将结构张量引入到扩散函数中。该方法在去除噪声的同时,保留了图像的细节。根据试验结果的比较,相对传统的滤波方法和P-M模型,本文方法的效果更加有效。
[1] GONZALEZ R C,WOODS R E.Digital image processing[M].Second edition.Beijing:Beijing Electronic and Industrial Press,2002.
[2] 冯象初,王卫卫.图像处理的变分和偏微分方程方[M].北京:科学出版社,2009.
[3] PERONA P,MALIK J.Scale-space and edge detection using anisotropic diffusion[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(8):629-639.
[4] 黄敦,游志胜.对彩色和亮度通道进行各向异性扩散的彩色图像分割[J].计算机工程,2002,28(6):166-169.
[5] CATTE F,COLL T,LIONS P,et al.Image selective smoothing and edge detection by nonlinear diffusion[J].SIAM Journal on Numerical Analysis,1992,29(1):182-193.
[6] 何宁,吕科,王袆雪.基于结构保持的MR图像运动伪影快速抑制方法[J].电子学报,2013,41(7):1319-1323.
[7] LIU F,LIU J B.Anisotropic diffusion for image denoising based on diffusion tensors[J].Journal of Visual Communication and Image Representation,2012,23(3):516-521.
[8] 王益艳,肖丹,钟超,等.基于结构张量扩散的改进PDE滤波算法[J].云南民族大学学报,2015,24(1):57-61.
[9] YOU Y L,XU W,TANNENBAUM A,et al.Behavioral analysis of anisotropic diffusion in image processing[J].IEEE Transaction on Image Processing,1996,5(11):1539-1553.
[10]GUICHARD F,MOISAN L,MOREL J M.A review of PDE models in image processing and image analysis[J].Journal de Physique IV,2002,92(12):137-154.
[11]郭敏,马远良,朱霆.基于偏微分方程的医学超声波图像去噪方法[J].计算机工程与应用,2007,43(15):243-244.
[12]陈龙,蔡光程.基于PDE的图像去噪方法[J].计算机工程与应用,2015,51(16):142-145.
[13]佟成,王士同,满丽红.一种改进的PDE图像去燥方法[J].计算机工程与应用,2010,46(15):176-178.
[14]WEICKERT J.Applications of nonlinear diffusion in image processing and computer vision[J].Mathematica Universitatis Comenianae,2001(1):33-50.
[15]熊保平,杜民.基于PDE图像去噪方法[J].计算机应用,2007,27(8):2025-2026.
Improved Anisotropic Diffusion Image Denoising Algorithm
XIAO Dan,HUANG Yuqing
(School of Information Engineering,Southwest University of Science and Technology,Mianyang 621010,China)
Image denoising is an important part of image processing,the denosing effect of classic image denoising algorithms,such as median filtering,Gaussian filtering,weighted average filtering,etc.,is not very ideal.With traditional methods,while removing noise,the edges of image may also become blurred. In recent years,partial differential equation (PDE) is a popular image processing method,and it has the characteristics of anisotropy,and it can well keep the edge while removing noise.An improved denoising algorithm is proposed based on the existing algorithms.The fixed threshold value in the traditional P-M operator is changed into an adaptive threshold,which is changing with the change of the gradient mode,and combining with the image structure tensor,a diffusion function featuring adaptive characteristics is constructed; it is isotropic in flat zone of the image,and conducive to smooth the noise while at the edge of the image,the model only diffuses along the tangential direction,and it is conducive to protect the image details.The tests show that the improved P-M model can improve the image denoising effect,meanwhile can also well keep the edge of the image.
Image denoising; Partial differential equation (PDE); Anisotropy; P-M model; Edge threshold; Structure tensor; Diffusion function
国家自然科学基金资助项目(61401379)
肖丹(1993—),女,在读硕士研究生,主要研究方向为视觉图像处理、目标检测与跟踪。E-mail:xd930922@163.com。 黄玉清(通信作者),女,硕士,教授,主要研究方向为无线控制及无线通信技术、图像处理与机器视觉、智能技术应用。 E-mail:hyq_851@163.com。
TH7;TP391
A
10.16086/j.cnki.issn1000-0380.201707001
修改稿收到日期:2017-03-27

