无速度传感器的异步电机矢量控制系统设计

杜丽霞

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)



无速度传感器的异步电机矢量控制系统设计

杜丽霞

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

为提高系统性能，文中将矢量控制技术和无速度传感器技术结合，设计了交流电机无速度传感器矢量控制系统。由于省去了速度传感器，系统减小了交流调速系统的复杂性，增强了系统的适应性，降低了成本。基于矢量控制和矢量坐标变换，建立了异步电机的数学模型。通过测量异步电动机定子电流矢量进行矢量控制。为控制异步电机的转矩，根据磁场定向原理分别控制异步电动机的励磁电流和转矩电流。Matlab/Simulink仿真结果表明，基于自适应模型的转速估计方法收敛速度快、估计精度较高，设计的无速度传感器矢量控制系统具有良好的静态和动态性能。

异步电动机；矢量控制；传感器

在高性能的交流电机矢量控制系统中，转速的闭环控制是必不可少的。通常，采用光电码盘等速度传感器来进行转速检测，并反馈转速信号[1-4]。由于速度传感器的安装给系统带来一些缺陷；精度越高的码盘价格越高，而且安装不当将会影响测速精度，电机轴上的体积增大会给电机的维护带来一定困难。取消矢量控制系统中的速度传感器能扩大矢量控制系统的应用范围，也能提高矢量控制系统的可靠性以及环境适应性。而设计的无速度传感器矢量控制系统无需检测硬件，有效提高了系统的可靠性，降低了系统成本，减小了系统的体积、重量以及电机与控制器之间的连线。因此采用无速度传感器的交流电机的调速系统具有广泛的应用前景。

为测量电动机的转子转速，本文测量异步电动机的电压和电流来估算电机转速，以实现无速度传感器矢量控制模型方法。在Matlab/Simulink平台中，建立了一个无速度传感器矢量控制系统，验证了该转速估计方法的有效性，仿真结果表明该系统具有良好的动静态特性和稳定性。

1 异步电机的物理模型

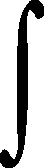
图1 三相异步电动机物理模型截图

1.1 异步电机的转子磁链电流模型

(1)异步电动机在静止坐标系上的电压方程式为

(1)

式中，usα、usβ为两相静止坐标系上两相定子绕组电压；urα、urβ为两相静止坐标系上两相转子绕组电压；isα、isβ为两相静止坐标系上两相定子绕组电流；irα、irβ为两相静止坐标系上两相转子绕组电流；ω为转子角速度；Rs、Rr为定子、转子一相绕组电阻；Ls、Lr为两相坐标系上定、转子绕组的自感；Lm为两相坐标系上同轴定、转子绕组间的互感。

(2)静止坐标系上两相转子绕组电流

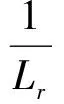
(2)

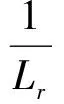
(3)

(3)异步电动机转子磁链电流模型方程。在静止坐标系电压方程式(1)中，令urα=urβ=0，且将式(2)和式(3)的关系代入，经整理后可得异步电动机转子磁链电流模型方程如式(4)和式(5)所示。

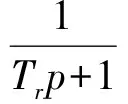
(4)

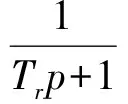
(5)

式中，Tr为转子电磁时间常数，Tr=Lm/Rr。

1.2 转子磁链电流模型

“云上交通遨碧空，峻岭险峰飘彩虹。磅礴乌蒙通天路，冲破关山万千重。”毕节的交通建设，脚踏实地蹄疾步稳，一个脚印一支歌。

按转子磁链定向二相旋转坐标系上的转子磁链电流模型来检测定子三相电流和转速计算转子磁链，三相定子电流经过3s/2r变换得到定子电流的励磁分量ism和转矩分量ist。并有异步电动机的如下矢量控制方程式[5]。通过式(7)，可以计算电动机转差ωs和定子频率ω1(ω1=ωr+ωs)

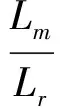
(6)

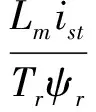
(7)

1.3 转子磁链的电压模型

根据异步电动机在静止坐标系上的物理模型的定子电压方程式(1)和转子电流方程式(2)和式(3)，可得出转子磁链的电压方程式(8)和式(9)，并构建转子磁链的电压模型如图2所示

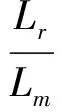
(8)

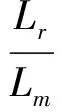
(9)

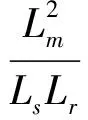
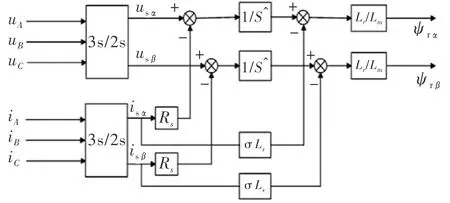
图2 转子磁链的电压模型

2 无速度传感器的矢量控制系统

2.1 无速度传感器的矢量控制系统模型

从电动机物理模型可以看出，电动机转速可以通过推算得到。无速度传感器的交流调速可避免速度传感器检测本身带来的误差[6]。模型参考自适应系统不需要进行性能指标的变换。模型参考自适应系统的控制器的参数随着对象特性的变化和环境的改变而不断调整, 从而使系统具有很强的适应能力。在满足控制要求的前提下, 建立一个合适的参考模型, 就能使自适应控制需要的时间足够小, 从而使被控对象参数变化过程比起参考模型和对象本身的时间响应要慢得多[7-11]。模型参考自适应控制系统的典型结构如图3所示。它主要由参考模型、可调系统和自适应机构组成, 其中可调系统包括被控对象和可调控制器[12]。

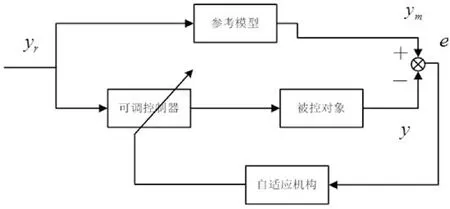
图3 模型参考自适应控制系统结构

按转子磁链定向转子磁链电流模型如图4所示，转速推算模块的组成如图5所示。

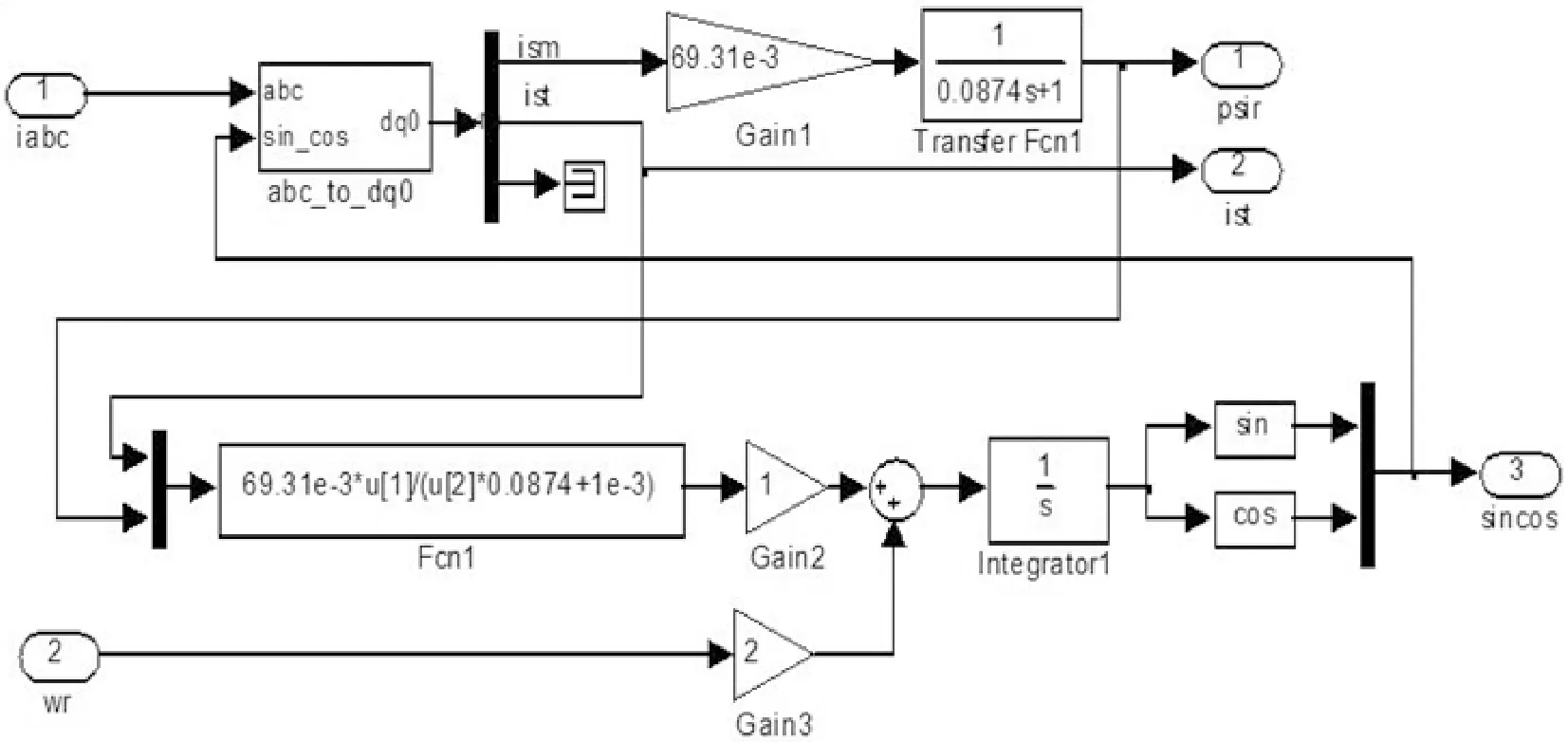
图4 按转子磁链定向转子磁链电流模型

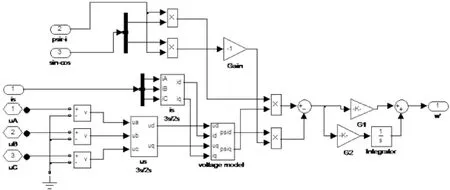
图5 转速推算模块

推算模块的1～4输入端，分别接入电动机定子三相电压和电流，经过3s/2r坐标变换，再有磁链电压模型如图2所示，计算得到ψαr、ψβr；推算模块利用矢量控制模型中转子磁链电流模型输出的磁链信号psir和sin-cos，经直角坐标变换得到转子磁链在α、β轴上的分量ψαr、ψβr，然后计算得到电动机转速。转速推算模块中PI调节器的参数取G7=4 500(G1)、G8=1.98(G2)[13]。以推算转速ωr代替电动机测量模块的转速值，观察无速度传感器的矢量控制系统对的控制效果，仿真模型如图6所示。

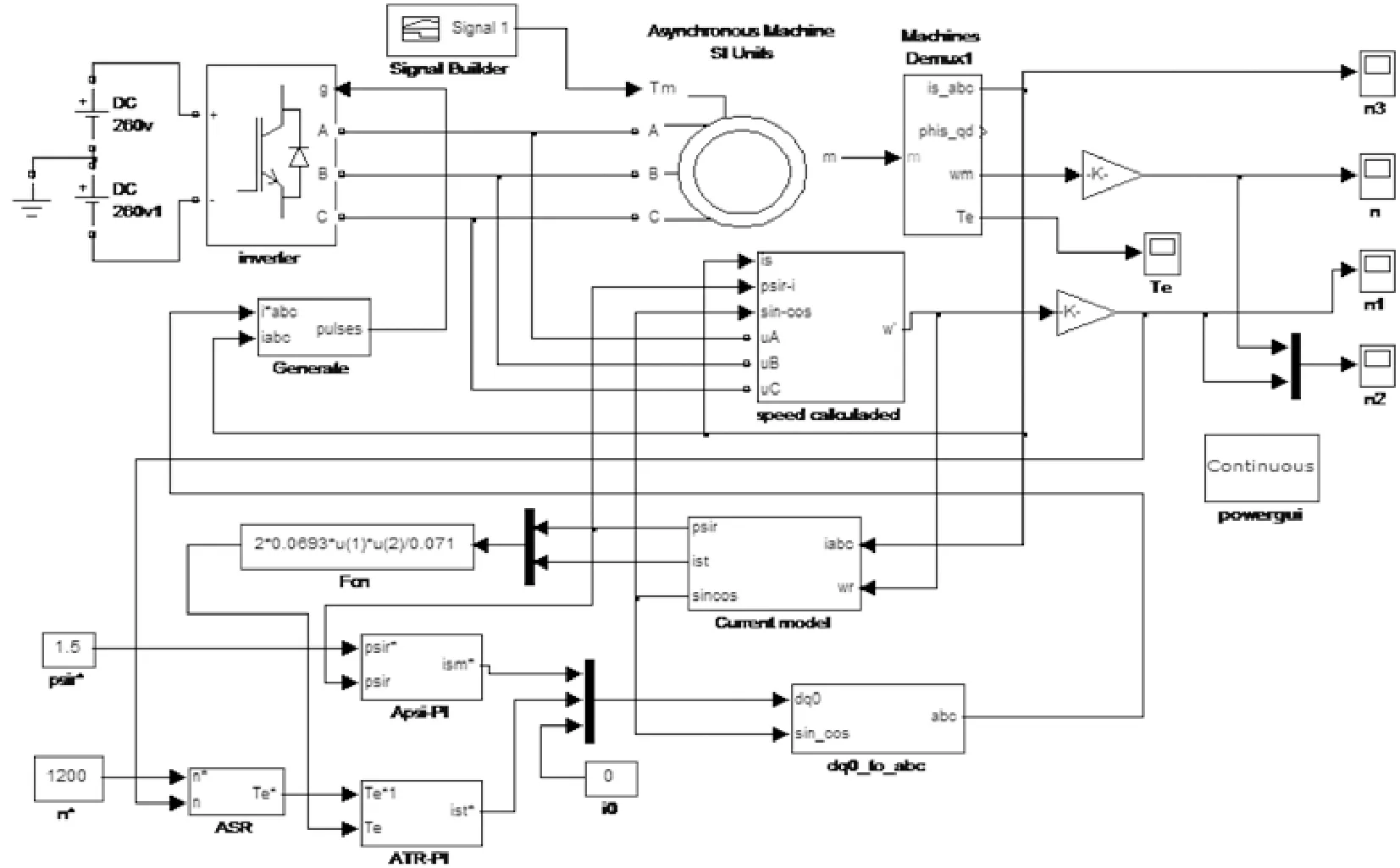
图6 无速度传感器的矢量控制系统仿真模型

3 无速度传感器的矢量控制系统仿真

3.1 正常转速下的仿真结果

在给定转速为1 200 r/min，空载启动，在t=0.5 s时加载55 N·m，运行至t=0.7 s时负载降为40 N·m。在矢量控制下，转速上升平稳，在0.35 s达到给定转速，在0.5 s加载55 N·m转速波形图如图7(b)所示，图7(c)所示为估算转速波形图。

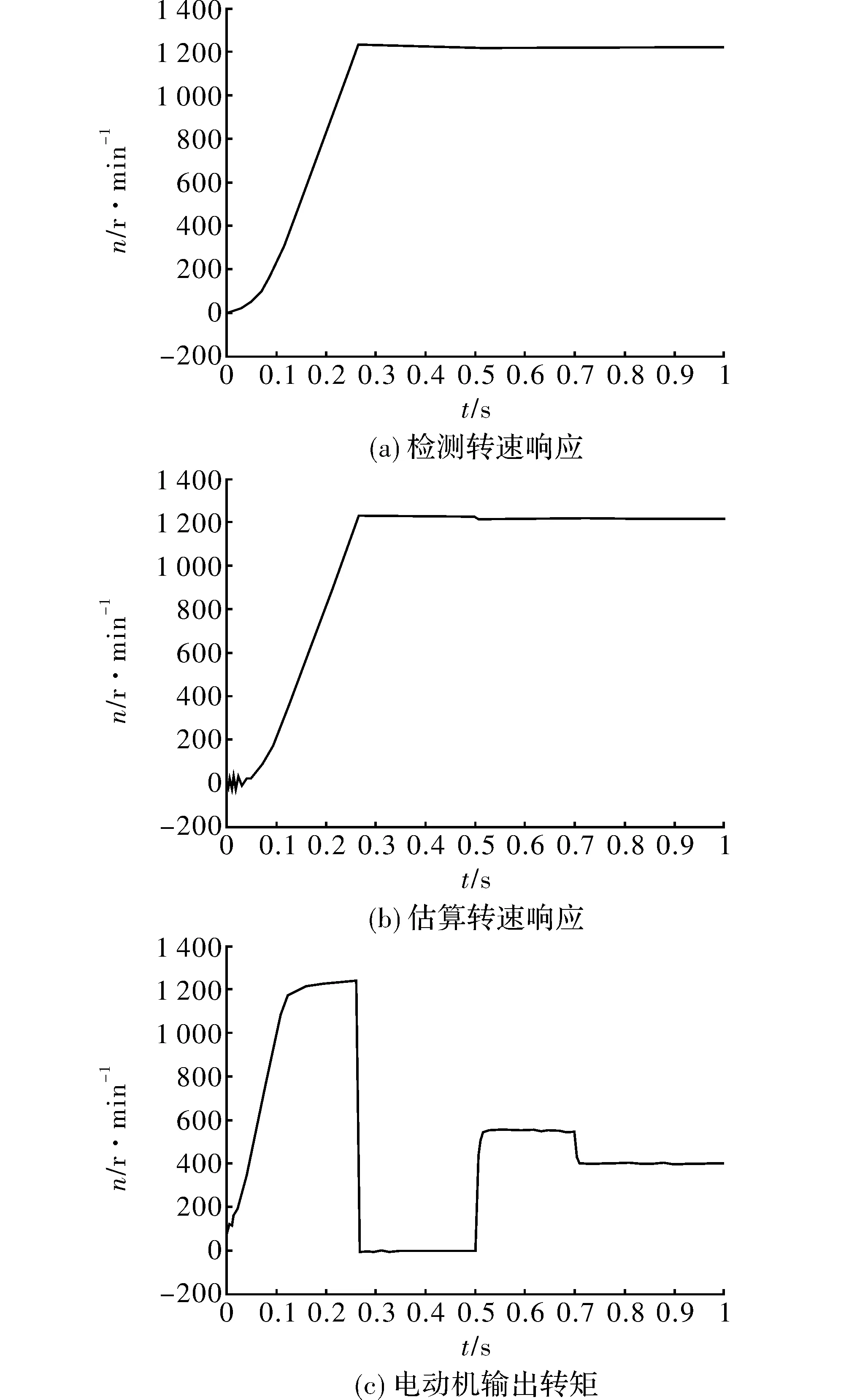
图7 无速度传感器的矢量控制系统仿真结果

由图可以看出，空载时转子速度在t=0.28 s时以达到稳定，收敛于速度给定值，在t=0.5 s时加载55 N·m，系统平稳运行，在t=0.7 s时负载将为40 N·m，系统响应在t=0.715 s时达到稳定，速度响应时间较短，输出较为平滑。

3.2 低转速下的仿真结果

在给定转速为200 r/min，空载启动，在t=0.6 s时加载55 N·m，系统仿真结果如图8所示。

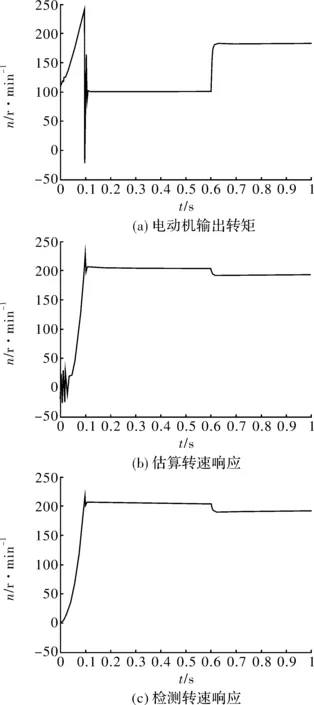
图8 低转速时仿真结果

在矢量控制下，0.1 s处输出转矩出现波动，很快又趋于平稳。转速上升平稳，在0.125 s达到给定转速。0.6 s时加入负载后，在0.615 s达到稳定转速，转速出现微弱的下降，但是速度误差在可控范围内。对于模型参考自适应系统，这也是说明其控制精度是比较好的。所以基于模型参考自适应系统的无速度传感器矢量控制系统可以同时适应高速、低速环境。

空载时转子速度在t=0.27 s时已达到稳定，收敛于速度给定值；在t=0.6 s时加载55 N·m，系统的响应在t=0.615 s时达到稳定，速度响应时间短，输出平滑。在启动0.1 s处出现较明显的转矩波动。无速度矢量控制系统在高速场合性能良好，但在低转速情况下，速度观测器不稳定，而且随温度升高而引起的电机参数变化。检测转速和推算转速中，带有小幅波动的是推算转速，较平滑的是测量模块输出的转速，两者差异较小。

4 结束语

本文以无速度传感器的矢量控制为研究对象。从仿真结果来看，无速度传感器矢量控制系统能够满足交流调速的可靠性和快速性的要求[14-15]。与有速度传感器矢量控制系统相比，减少了检测装置，避免了速度传感器检测本身带来的误差，提高了精度，同时也降低的设备成本。基于模型参考自适应的无速度传感器矢量控制系统能够准确地观测出电机的实际速度，转速估算的速度误差较小，当速度发生变化时输出转速曲线响应较快且跟踪性能良好。

[1] 李自成.感应电机无速度传感器矢量控制系统的研究[D].武汉:华中科技大学,2005.

[2] 冯垛生.无速度传感器矢量控制原理与实践[M].北京:机械工业出版社,2001.

[3] 林森.异步电机无速度传感器矢量控制系统研究[D].长沙:中南大学,2008.

[4] 洪乃刚.电力电子、电机控制系统的建模和仿真[M].北京:机械工业出版社,2010.

[5] 王志新.电机控制技术[M].北京:机械工业出版社,2010.

[6] 陈伯时.电力拖动自动控制系统[M].3版.北京:机械工业出版社,2003.

[7] 洪乃刚.电力电子和电力拖动控制系统的Matlab仿真[M].北京:机械工业出版社,2006.

[8] 王兆安.电力电子技术[M].北京:机械工业出版社,2000.

[9] 韩如成,潘峰,智泽英.直接转矩控制理论及应用[M].北京:电子工业出版社,2012.

[10] 陈伟昌,王孝洪,田联房.基于DSP的无速度传感器异步电机矢量控制[J].电机与控制应用,2015 (3):20-23.

[11] 刘稳健,蔡华杰,朱维杰.基于参数识别的PMSM无位置传感器矢量控制[J].电子技术应用,2016 (8):67-69.

[12] 李旭春,张鹏,赵非.改进EKF的异步电机无速度传感器矢量控制[J].电机与控制学报,2013,17(9):24-29.

[13] 程启明,王映斐,薛阳,等.采用定子电阻辨识和无速度传感器的异步电机直接转矩控制模糊系统[J].高电压技术,2012,38(3):704-711.

[14] 杨泽斌,汪明涛,孙晓东.基于转矩绕组无功功率MRAS的无轴承异步电机无速度传感器矢量控制系[J].四川大学学报:工程科学版,2014 (2):140-146.

[15] 姜宏丽,宗伟,刘其辉,等.改进电压模型的异步电机无速度传感器矢量控制[J].电气传动,2015,45(2):8-12.

Design of Vector Control System for Asynchronous Motor without Speed Sensor

DU Lixia

(School of Electronic and Information Engineering, Lanzhou Jioatong University, Lanzhou 730070, China)

A vector control system for AC asynchronous motors is designed to improve the system performances by combining vector control technique and the technology without speed sensors. The complexity, the environmental adaptability and the cost of system are improved due to the absence of speed sensors. The mathematical model of asynchronous motor is established based on vector control and vector coordinate transformation. The vector control is realized by measuring current vector of stator. In order to control the torque of AC asynchronous motors, the excitation and the torque currents are controlled according to the magnetic field oriented principle, respectively. The Matlab/Simulink results show that the model reference adaptive speed estimation has the advantages of fast convergence speed and high estimation accuracy. The designed speed-sensorless vector control system has good static and dynamic performances.

asynchronous motor; vector control; sensor

2016- 09- 13

国家自然科学基金(61366006)

杜丽霞(1968-)，女，教授。研究方向：电子技术，自动化。

10.16180/j.cnki.issn1007-7820.2017.07.030

TM343

A

1007-7820(2017)07-110-04