基于ADAMS抽油机的运动学仿真与优化设计
郭 锐,褚超美
(上海理工大学 机械工程学院,上海 200093)
基于ADAMS抽油机的运动学仿真与优化设计
郭 锐,褚超美
(上海理工大学 机械工程学院,上海 200093)
为提高抽油机的工作效率和获得较好的工作性能,针对抽油机的主要尺寸进行优化设计。通过对抽油机工作原理的分析,确定了设计变量、目标函数和约束条件,建立以最大扭矩因数为目标函数的参数化数学模型,采用Adams仿真软件对该机构进行仿真,并对参数进行了优化计算。结果表明,优化后的最大扭矩因数比优化前降低了42.7%,抽油机的工作效率和工作性能得到明显改善。
抽油机; 运动学仿真; 扭矩因数; 优化设计
抽油机是油田中的设备,游梁式抽油机结构简单、可靠性好、耐久性高和维修方便,但是由于其四连杆的结构特点,使它存在着悬点扭矩大峰值波动剧烈,载荷冲击大等缺陷[1],这些缺陷使抽油机运动平衡性差、耗油大。为解决这些缺陷,以往通常采用两种简化模型:一种是曲柄等效模型;另一种则是平面等效模型[2-3]。但是这两种方法都无法准确描述抽油机的真实运动。虚拟样机技术可以直观清晰的模拟抽油机在真实情况下的运动变化,同时利用优化设计,为解决这类问题提供了新的途径[2-4]。文献[5]利用Adams对双驴头抽油机进行了运动学仿真,验证了模型结构的合理性,为抽油机的优化设计理论提供了理论基础。本文利用UG建立虚拟样机的结构模型,在Adams中进行参数化设计[6-7],以最大扭矩因数为目标建立优化设计模型,利用Adams/Insight测量设计变量对目标因数的敏感度,进行变量筛选,同时对模型进行优化计算,优化了模型主要结构,改善了游梁式抽油机综合性能。
1 游梁式抽油机的运动学分析
抽油机四连杆机构主要由曲柄、连杆、横梁、游梁以及驴头等组成。曲柄的主要作用是传递输出轴扭矩;连杆的作用是连接曲柄与横梁并传递曲柄力矩;横梁是连杆和游梁连接的中间部件,游梁是抽油机的主要承载部件,在抽油机正常工作时,游梁同时承受悬点载荷、连杆拉力以及支架对游梁的反作用力等载荷,驴头的作用是保证抽油时光杆始终对准井口中心位置。如图1所示,由余弦定理、正弦定理和角度关系可知[9-10]
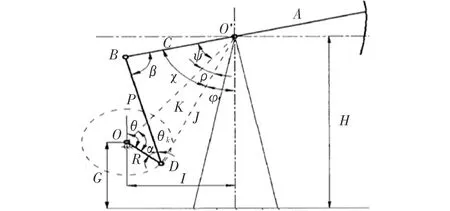
图1 抽油机的工作原理简图
(1)
(2)
α=β+ψ-θk
(3)
游梁摆动的角速度为[11]
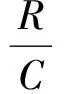
(4)
则悬点的速度为
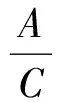
(5)
游梁摆角的加速度可由角速度ωb对时间的导数求出
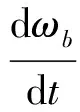
(6)
悬点的加速度就是驴头与悬点的切向加速度,由比例关系可知
a=Aεb
(7)
扭矩因数为悬点的速度与曲柄的旋转角速度的比值,其表达式为
(8)
其中,R为曲柄半径;P为连杆长度;C为游梁后臂的长度;A为游梁前臂长度;K为极距;J为曲柄销中心到游梁支撑中心的距离;α为R与P的夹角;β为P与C的夹角,称为传动角;ω为曲柄旋转的角速度;θk为DO与OO′的夹角;ψ为OO′与BO′的夹角。
2 优化设计数学模型的建立
2.1 设计变量的确定
抽油机设计变量主要有曲柄R,连杆P与后梁C,曲柄与水平面的初始位置角δ,如表1所示。

表1 设计变量的初始值与设计范围
2.2 约束条件的确定
抽油机有诸多条件的限制,根据需要主要考虑几何尺寸的与运动参数约束[16]。
(1)曲柄与水平面初始位置夹角的变化范围
2°<δ<20°
(2)各杆之间的相对尺寸限制为
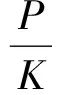
(3)曲柄四连杆机构存在的条件为
R+P (4)保证K为最长杆,R为最短杆,即有 P 2.3 建立目标函数 其中,D为约束条件下的X取值范围。 在UG中建立抽油机的三维模型如图2所示。 图2 游梁式抽油机的三维模型 将模型导入Adams中,定义材料,添加约束[15],将模型简化为四连杆机构,选取关键的点进行参数化[6],添加驱动,进行仿真。所得的扭矩因数变化曲线如图3所示。 图3 扭矩因数的变化曲线 在图3中可以看出扭矩因数在仿真时间内为正弦变化,符合抽油机扭矩变化规律,证明建立的抽油机模型合理。图中悬点在下死点时扭矩矩因数有最大值,且最大扭矩矩因数为1 830.5 mm。 4.1 Adams/Insight实验设计 Adams/Insight的主要作用是变量筛选,即当一个系统中有多个变量时,通常只有设计变量小部分是重要的,筛选试验可以用来 辨别这些重要的变量及这些变量对于系统性能影响的程度,实验结果如表2所示。 表2 各项拟合指标的值 经过16次迭代仿真后,对仿真结果以标准方差进行拟合,R2和R2adj表示拟合的好坏,R2在0~1 之间,越大越好,好的合应该>0.9。R2adj表示通常 从导出的Web页面可以分析出各个设计变量对优化目标的影响程度[13]。其中,曲柄长度R对扭矩因数的影响为80.66%,灵敏度最高,曲柄与水平面初始位置的夹角δ影响为1.32%,灵敏度最小,如图4所示。 图4 变量对目标函数的影响程度 4.2 基于ADAMS的迭代优化设计 通过所建立的参数化数学模型,建立了3个优化设计变量,并根据设计要求与实际情况选定了初始值与取值范围,添加约束条件,进行优化设计[8],优化结束后,得出优化结果如图5与图6所示。 图5 优化前后悬点加速度变化曲线 图6 优化前后的扭矩因数变化曲线 悬点的加速度可以在一定程度上反映抽油机运动的平顺性,图5可以看出优化后悬点的加速度明显减小,加速度最大值比优化前降低了11.5%,悬点峰值波动有所减小。图6描述了优化前后扭矩因数的变化,优化前最大的扭矩因数为1 830.5 mm,优化后最大扭矩因数的值为1 047.8 mm,比优化前降低了42.7%。优化后的最大扭矩因数明显降低,抽油机的工作性能得到了一定的改善。 针对抽油机的在实践中存在的问题,本文建立了基于Adams的游梁式抽油机的参数化数学模型,对抽油机四杆机构的几何参数、悬点运动规律、最大扭矩因数等一系列问题作了详细的分析,为抽油机的动态仿真提供了理论基础。针对目标函数的分析,本文采用了=“仿真分析-实验设计-优化分析”的思路,提高了设计改造的效率和准确性。从优化结果来看,优化后的抽油机的扭矩因数明显降低,运动效率和平稳性得到了一定的改善。但是,本文主要以抽油机的运动学分析为主,还需要对抽油机动力学分析上做深入的探讨才能更好的解决实际问题。 [1] 张晓东,贾国超.关于我国抽油机发展的几点思考[J].石油矿场机械,2008,37(1):24-27. [2] 徐中文.抽油机设计软件开发及优化设计[D].大庆:大庆石油学院,2006. [3] 连颍.双驴头抽油机的动力学分析[D].南京:南京理工大学,2007. [4] Rowlan O L,Meeoy J N,Podio A L.Best method to balance torque loadings on a Pumping Unit gearbox [J].Journal of Canadian Petroleum Teehnology,2005,44(7):27-32. [5] 周庆龙,邹振华.双驴头抽油机的优化设计与运动学分析[J].石油矿场机械,2012,41(6):21-25. [6] 骆华锋,栾庆德.游梁式抽油机实体建模及仿真分析[J].石油矿场机械,2008,37(12):22-24. [7] 赵武云,史曾录,戴飞.Adams2013基础与应用实例教程[M].北京:清华大学出版社,2015. [8] 李宾元,肖芳淳,黄春燕.抽油机四连杆机构参数的多目标函数优化的探讨[J].西南石油学院学报,1987,9(4):48-56. [9] 张建军,李向齐.游梁式抽油机设计计算[M].北京:石油工业出版社,2005. [10] Rowlan O L,Meeoy J N,Podio A L.Best method to balance torque loadings on a pumping unit gearbox[J].Journal of Canadian Petroleum Teehnology,2005,44(7):27-32. [11] 万邦烈.采油机械的设计计算[M].北京:石油工业出版社,1986. [12] 李仁兴.游梁式抽油机运动和动力学仿真及优化设计[D].西安:西安理工大学,2005. [13] 徐中文.抽油机设计软件开发及优化设计[D].大庆:大庆石油学院,2006. [14] 曹惟庆.平面连杆机构分析与综合[M]. 北京:科学出版社,1989. [15] 黎业吃.游梁式抽油机CAD 系统的研制[D].南京:东南大学,2001. [16] 杨萍萍,冯长凯.可展开伸缩套管式伸展臂结构设计与分析[J].电子科技,2008,21(9):8-11. Kinematics Simulation Analysis and Optimization Design of Pumping Unit Based on ADAMS GUO Rui,CHU Chaomei (School of Mechanical Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China) The main sizes of pumping unit is optimized to enhance the work efficiency and to get the better work capability. By analyzing working theory of the pumping unit, the designing variables, the constraint condition and the objective function are analyzed. In order to gain the maximum torque factor, a mathematics model of the pumping unit parameter optimization design is put forward and simulated using Adams and the same parameters are also optimized. The results show a decrease of maximum torque factor of 42.7% after optimization with notably improved working efficiency and capability of pumping unit. pumping unit; kinematics simulation; torque factor; optimal design 2016- 07- 22 郭锐(1989-),男,硕士研究生。研究方向:汽车变速器零部件的仿真与优化。褚超美(1958-),女,教授。研究方向:汽车变速器设计与开发。 10.16180/j.cnki.issn1007-7820.2017.07.012 TP391.9 A 1007-7820(2017)07-044-04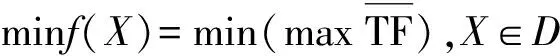
3 建立参数化建模与仿真分析
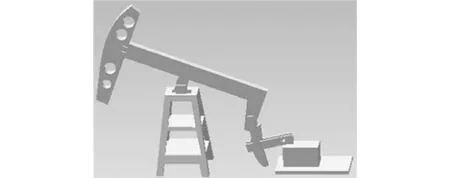
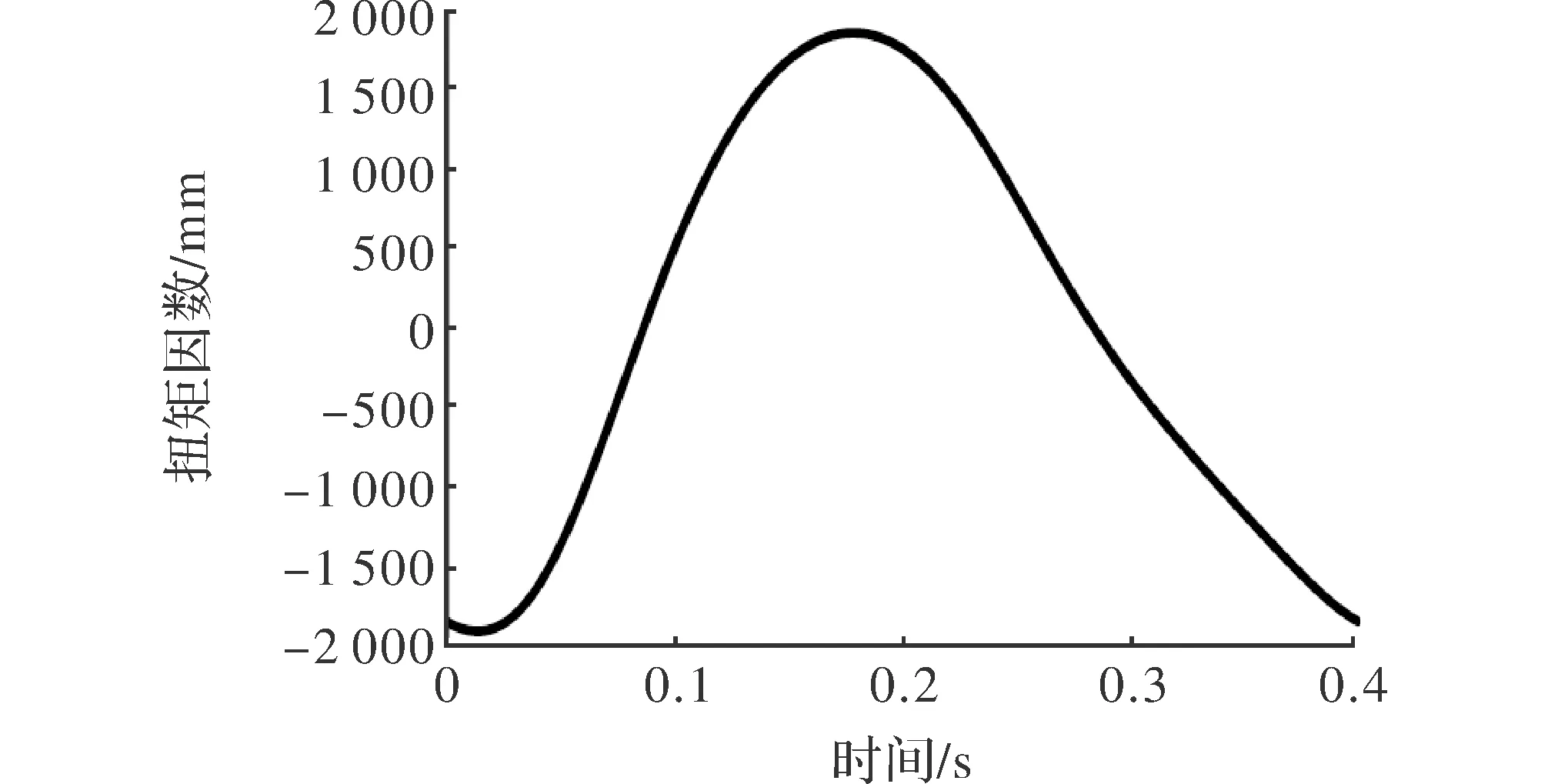
4 抽油机的优化设计

5 结束语

