垂向航行体水下多元阵测量精度仿真算法

张 旭，韩 旭，辛 健

(1.解放军91550部队，辽宁 大连 116023;2.解放军92493部队博士后科研工作站, 辽宁 大连 116023)

垂向航行体水下多元阵测量精度仿真算法

张 旭1,2，韩 旭1,2，辛 健1

(1.解放军91550部队，辽宁 大连 116023;2.解放军92493部队博士后科研工作站, 辽宁 大连 116023)

水声定位；多元阵；精度仿真算法；水下垂向航行体测量

0 引言

水声定位技术是水下航行体运动轨迹测量的重要技术手段，近年来随着水声定位与惯性导航集成、宽带信号处理、多阵元数据融合等技术的不断进步，针对AUV、UUV等水下航行体的测量已有高精度、集成化、系列化的水声定位产品(如英国Sonardyne Ranger2，挪威Kongsberg Hipap，法国Ixsea GPAS，法国Ixsea Ramses)，且在海洋工程领域取得了广泛的应用[1-4]。然而，水下垂直航行体的运动与水平航行体有较大差异，具有速度快、历时短、工况复杂、平台不易搭载等特点，使得“询问-应答”测量体制下的传统水声测量系统在技术手段上难以满足垂直航行体的测量设计要求。在近年来国内的工程实践中，哈尔滨工程大学研制的图像声纳系统首次实现利用主动声纳系统对水下垂向航行体进行测量，根据声学图像中提取出的目标距离和方位信息解算其运动轨迹[5]，但这种方式在物理机制上仍具有较大的局限性，难以在有空泡覆盖的条件下达到较高的测量精度和数据率。为实现测量能力的突破，国内相关院所最近开始将研究的重点转向合作目标式测量，并已开展相关的论证研究工作。

与测量技术手段的发展相对应，长基线测量的精度分析方法也正在从简单构型的解析到多元复杂阵型的建模与仿真。在传统的“询问-应答”测量体制下，直线阵、圆弧阵、等边三角形阵等阵型结构简单，相对误差较大[6-7]，圆形阵虽能达到较好的测距和测向精度，但阵元构型设计复杂[8]，相比之下四元阵则因有较好的精度且易于组合布阵成为工程中常用的方案，关于其测量特性已通过多种解析和仿真模拟方法取得了较为清晰的认识[9-11]。然而，当多阵元组成复合型测量阵时，测量精度的解析变得十分困难，往往需要结合仿真算法实现，现有关于复杂测阵的设计大多针对水平航行体[13-14]，而对于有合作目标条件下的水下垂向航行体测量问题，误差源和误差传递过程均发生了较大变化，目前尚无相关报道，需要重新设计精度仿真方法。本文针对此问题，在长基线定位模型的基础上提出一种基于合作目标的水下多阵元测量精度仿真算法。

1 测量工况与模型

假设航行体随运载平台在有限海域内匀速移动中随机释放，释放后航行体做高速垂向运动直至出水。航行体上加装合作声信标，在释放后开始工作，由布设在平坦海底(水深取60 m)的若干接收阵元组成矩形测量阵(运载平台可拖带一个辅助的浮体式阵元)，进行长基线定位测量。

以测试海区海底中心点O为原点建立测量坐标系，OX轴指向运载平台移动方向(与矩形长轴相平行)，OY轴铅直向上，指向海面，OZ轴与OX轴、OY轴共同构成右手坐标系(见图1)。

(1)

(2)

2 测量精度仿真算法

由于待测目标在有限海区内随机释放，因此需要对测试区域中每一个三维格点的精度进行测算。以下根据蒙特卡洛数值方法设计仿真算法，每个格点取大子样重复计算，每次取样中模拟实际工况组合代入各项误差，再通过最小二乘迭代求解，可实现全海域三维空间的误差估计，进而用于多阵元复杂基阵构型的测量精度分析。

2.1 误差源变量

为实现上述测量模型的精度分析，引入以下误差源变量：

2.2 测量值估算

将测量模型进行线性化处理，以代入误差源变量：

Δx=x0-x,Δy=y0-y,Δz=z0-z。

其中，x0、y0、z0表示由合作目标标记的迭代初始位置坐标。

上式可表示为矩阵形式：

ΔR=AΔX

(4)

式中,

(5)

2.3 误差源代入

为了在仿真中模拟工况条件和代入误差，在仿真算法中有以下几个关键过程(仿真计算流程见图2)：

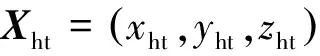
3 仿真结果

以下选取一种典型的多元海底阵构型，对上述算法进行验证。

3.1 误差分布特性

基阵由16个阵元构成，呈菱形分布在水深60m的海底，基线长度设为300m，基阵覆盖区域可视为9个边长为300m的四元阵的组合。假设合作声信标的指向性开角为60°，近程传输时计算点附近的盲区由指向性开角限定，远程传输时的最大接收距离设为1 000m。计算区域设为1 500m×1 500m，水平格点设为10m×10m，垂向计算区域设为30～60m(60m处为海面)，垂向格点设为1m，每个格点重复取样次数设为1 000次。通过仿真计算得到测试区域标准差的三维矩阵，为了便于分析误差分布情况，采用在Y轴典型深度上“切片”的方式，以X-Z平面的标准差分布呈现计算结果。图3给出了水深45 m处X、Y、Z三个方向上的标准差分布(误差变化通过图中色标反映)，基阵位置由图中黑色圆点表示。

由图3所示，本文提出的仿真算法能够得到多组四元阵组合测量条件下的误差精细结构，而随着阵元构型的复杂化，类似的结果对于解析方法是难以达到的。同时，由于仿真算法基于统计学假设，误差源的分布规律接近工程实际，通过大子样重复计算滤除了小概率因素，得出的结果在统计学意义上是较为稳定的。

从误差分布的特性来看，在这种几何构型条件下，阵内定位精度明显好于阵外定位精度，且水平定位精度要好于垂向定位精度。对于水平方向，X方向和Z方向的定位精度相当，阵内标准差的置信区间均为0.12～0.16 m(以90%的置信概率计算)，均值为0.13 m，而阵外1倍基线长度以外的区域标准差迅速增大到1.0 m以上；对于Y方向，阵内标准差的置信区间为0.60～1.20 m(以90%的置信概率计算)，均值为0.70 m，阵元附近受近程盲区影响大于周边区域，阵外1倍基线长度以外的区域标准差迅速增大到3.0 m以上。这就意味着，完全依靠海底布设的多元阵，即可实现对阵内任意位置释放的航行体进行三维轨迹测量，水平方向可获取亚米级精度，垂直方向上可获取米级精度。

3.2 基线变化的影响

在16阵元菱形阵的基础上，考虑将原基线长度300 m增加到500 m，其他参数设置不变，以检验基阵长度变化对基阵测量效果的影响。在此条件下重新仿真计算得到的标准差分布如图4所示。

比较图3和图4可以看出，在阵元数量不变的条件下，基线拉长所带来的影响是在每个测量点的有效接收距离内参与解算的阵元数量减少了。这种变化直接在标准差分布中得以反映。以90%的置信概率计算，X方向和Z方向阵内标准差的置信区间分别为0.15～0.21 m和0.16～0.22 m，均值分别为0.17 m和0.18 m,精度整体下降了约0.04～0.05 m；Y方向阵内标准差的置信区间为0.86～1.34 m，均值为1.12 m，精度下降了约0.42 m。可见，基线长度从300 m增加到500 m，使得测量阵覆盖范围由900 m×900 m扩大到1 500 m×1 500 m，但与此同时X、Y、Z三个方向的定位精度都有不同程度的下降，这在阵元附近的盲区更加明显。

3.3 浮体阵元的影响

完全由海底阵元构成的测量基阵在几何构型上为多组四棱锥形。若考虑在上述测量阵型的基础上，加入运载平台拖带的一个浮体式阵元，阵元在运载平台后方，拖带缆长100 m，垂直航向的随机摆动满足标准差为20 m的正态分布，随海面波浪的起伏满足标准差为1 m的正态分布，此时的阵元构型由共面式分布变为立体式分布。在其他计算参数与3.1节中采用相同的设置的条件下，在仿真算法中加入该浮体阵元，通过仿真计算得到的标准差分布如图5所示。

比较图3和图5可以看出，增加浮体阵元后使标准差的分布样式发生了明显的变化。在相对于计算点X轴负向布放的浮体阵元使X方向和Y方向的高精度测量区域向X轴正向扩展，而对于Z方向的标准差影响不大。以90%的置信概率计算，X方向和Z方向阵内标准差的置信区间分别为0.11～0.14 m和0.12～0.15 m，均值分别为0.12 m和0.13 m,与不加浮体阵元相比精度整体提高了约0.01 m；Y方向阵内标准差的置信区间为0.57～0.90 m，均值为0.66 m，与不加浮体阵元相比精度提高了约0.04 m。从高精度区域的覆盖范围来看，加浮体阵元后使阵内X方向定位标准差优于0.15 m的区域从84.9%增加到94.8%，Z方向从85.0%增加到86.9%，使Y方向定位标准差优于0.7 m的区域从48.4%增加到66.9%。可见，在多组四棱锥形几何模型的基础上，增加一个非共面的补充阵元使大面积测试区域的标准差分布发生了明显变化，这也充分说明了多阵元测阵条件下阵元数量和构型变化对精度分布的复杂影响。

4 结论

[1]孙大军, 郑翠娥. 水声导航、定位技术发展趋势探讨[J]. 海洋技术学报, 2015, 34(3): 64-68.

[2]李守军, 包更生, 吴水根. 水声定位技术的发展现状与展望[J]. 海洋技术, 2005, 24(1): 130-135.

[3]Paull L, Saeedi S, Seto M, et al. AUV Navigation and Localization: A Review[J]. IEEE Journal of Oceanic Engineering, 2014, 39(1): 131-149.

[4]Lee P M, JUN B H. Pseudo long base line navigation algorithm for underwater vehicles with inertial sensors and two acoustic range measurements[J]. Ocean Engineering, 2007, 34: 416-425.

[5]娄汉泉, 李铁. 海上靶场测控系统技术特点及应用[J]. 飞行器测控学报, 2010, 29(5): 6-10.

[6]顾晓辉, 王晓鸣. 用双直角三角形阵对声目标定位的研究[J]. 声学技术, 2003, 22(1): 44-48.

[7]孙书学, 顾晓辉, 孙晓霞. 用正四棱锥形阵对声目标定位研究[J]. 应用声学, 2006, 25(2): 102-108.

[8]祝龙石, 庄志洪, 张清泰. 利用圆阵实现声目标的全空域被动定位[J]. 声学学报, 1999, 24(2): 204-209.

[9]贾云得, 冷树林, 刘万春，等. 四元被动声敏感阵列定位模型分析和仿真[J]. 兵工学报, 2001, 22(2): 206-209.

[10]程翔, 张河. 高低四元阵定位算法及其精度分析[J]. 探测与控制学报, 2006, 28(4): 12-14.

[11]金磊磊, 马艳. 任意四元阵的定位盲区讨论及误差影响[J]. 探测与控制学报, 2015, 37(2): 90-94.

[12]Tremois M, Le Cadre J P. Target Motion Analysis with Multiple Arrays: Performance Analysis[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32: 1030-1045.

[13]于平, 吴波. 长基线水声定位基阵阵形优化设计[J]. 舰船电子工程, 2015, 35(5): 125-129.

[14]刘利生, 吴斌, 吴正容，等. 外弹道测量精度分析与评定[M]. 北京: 国防工业出版社, 2010: 123-188.

Underwater Vertical Vehicle Measuring Accuracy Simulation Based on Seabed Multielement Array

ZHANG Xu1,2, HAN Xu1,2, XIN Jian1

(1.Unit 91550 of PLA, Dalian 116023, China; 2.Postdoctoral Scientific Research Station in 92493 unit of PLA, Dalian 116023, China)

underwater acoustic positioning; multi element array; accuracy simulation algorithm; underwater vertical vehicle measuring

2016-12-23

张旭(1982—)，男，黑龙江萝北人，博士，研究方向：水下测量技术。E-mail:yanxp2012@aliyun.com。

TJ760.6

A

1008-1194(2017)03-0086-06