海面电磁缩比测量的替代模型
赵 晔,张丹萌, 曹 屹
(1.延安大学物理与电子信息学院,陕西 延安 716000;2.安徽大学电气工程与自动化学院,安徽 合肥 710071;3.西安机电信息技术研究所,陕西 西安 710065)
海面电磁缩比测量的替代模型
赵 晔1,张丹萌2, 曹 屹3
(1.延安大学物理与电子信息学院,陕西 延安 716000;2.安徽大学电气工程与自动化学院,安徽 合肥 710071;3.西安机电信息技术研究所,陕西 西安 710065)
针对介电常数缩比条件要求的测试海水温度和盐度的问题,提出了海面电磁缩比测量的替代模型。该模型采用淡水替代海水进行海面缩比测量,可以避免实验室内采用海水测量时理论温度和盐度的不可能性和海水对造波设备的腐蚀。数值仿真表明,中等入射角下,采用淡水替代海水进行海面缩比测量在反射系数中所引入的误差不到1 dB。此外,缩比模型和原型海面之间的散射系数、散射场模值的空间分布、杂波序列及多普勒谱的比较也表明,海面电磁缩比测量的替代模型具有一定的可行性。
海面;海水介电常数;缩比模型;散射系数
0 引言
电磁缩比测量技术已经得到了广泛的应用和发展[1],Stratton在1941年提出了最经典的电磁相似律[2],Sinclair在1948年总结并给出了电磁系统的缩比理论[3],这种电磁缩比测量技术曾经成功地应用于天线测量[4],以及金属目标的电磁散射测量[5]。缩比测量方法以电磁相似理论和严格的相似性关系为基础建立缩比测量实验场对缩比目标在特定波段进行相关测量,其在技术和经济方面具有很强的优势。国内外很多研究机构建立了电磁缩比测量的实验室,如美国陆军高级仿真中心、美国马萨诸塞州立大学亚毫米波技术实验室(STL)、美国雷锡恩(Raytheon)公司导弹系统分部、英国国家无线电缩比模型实验室[6]等。国内如北京环境特性研究所、国防科技大学和西安机电信息技术研究所等。此外,国内上海无线电设备研究所在海水缩比模型测量方面也取得不少成果。
缩比模型已经广泛地应用于工程测量中,可以为实验分析或设计提供必要的信息。尽管在制作缩比模型本身和提高测量的精度中存在许多问题,缩比测量模型的确能够为目标雷达散射截面的预估提供一个重要的方法。缩比模型测量试验的理论依据是相似理论[7-8],根据电磁相似理论,被测模型与原型必须在几何外观、尺寸大小及材料的介电特性等方面满足一定的相似条件。由于介质材料具有频率色散特性,其介电常数会随着频率的变化而发生改变,在缩比模型系统的工作频率下,所需的模型材料在自然界中一般不容易找到,因此需要利用现有的常用材料进行混合制备。介质材料的制备需要以混合介质理论为依据,并反复进行试验测量,最终得到与目标材料偏差较小的材料。
海杂波实测是研究海杂波电磁散射特性的主要手段[9]。由于海面及其周围的环境难以测定和定量描述,因此,测量得到的海面散射回波数据稳定性不高,为了提高海杂波测量的精度,国内外很多研究机构开始利用造波技术在实验室内对海浪进行模拟和相关测试[10-12]。在实验室内模拟海浪并对其进行测量研究,需要解决被测缩比海面模型与实际海面在几何外观上相似的问题,此外,海水的介电常数是关于海水温度、盐度和入射频率的复杂函数,所以,如何保证海水介电常数在不同入射频率下保持一致是一个非常棘手的问题。理论上,可以根据海水的介电常数模型推导出海水介电常数所满足的缩比条件,但是,介电常数缩比条件要求的测试海水温度和盐度是不切实际的。本文针对此问题,提出了海面电磁缩比测量的替代模型。
1 海水介电常数缩比条件分析
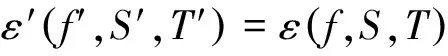
根据单Debye模型[13],将海水的介电常数写成如下形式:
(1)
式中,ω=2πf为电磁波频率,τ为张弛时间,ε0=8.854×10-12为真空介电常数,γi为离子电导率,εs为静态介电常数。静态介电常数、张弛时间和离子电导率是和海水温度T和盐度S相关的量。
假设缩比模型和原型的海水介电常数满足相似条件,与海水介电常数有关的各物理量满足以下比例关系[14]:
ε′=ε,ω′=pω
(2)
式中,p为缩比因子,Xε,Xτ和Xγ是比例系数;带撇的量和不带撇的量分别表示与缩比模型相和原型相关的量。
根据式(1),缩比模型的介电常数可表示为:
(3)
很明显,如果缩比模型与原型的介电常数满足相似条件,则可以得到比例系数为:
Xε=1,pXτ=1,Xγ/p=1
(4)
即有
(5)
根据上面的推导,模型海水盐度S′和温度T′的求解方法为:首先根据实际海水的温度及盐度得到原型海水的相关参量:张弛时间、静态介电常数和电导率;然后根据式(5),计算模型海水的张弛时间、静态介电常数和电导率;最后联立求解下面的非线性方程组
(6)


表1 不同缩比因子时模型海水的温度和盐度
考虑到理论上得到的模型海水的温度和盐度,在实际实验室中是无法达到的,并且为了减小对造波设备的腐蚀,造波池内通常用淡水替代海水进行海面模拟于测量。
2 淡水替代海水的可行性分析
下面定量分析利用淡水替代海水时,从而造成介电常数违背相似性条件所引入的误差,这种误差首先体现在反射系数中,具体可以表示为:
(7)
式中,Rwater,Rsea表示淡水和海水的反射系数。
图1分析了不同缩比因子下淡水(S=0,T=20 ℃)替代海水(S=35 ppt,T=20 ℃)时所引入的误差,其中原型系统的入射频率为2GHz,入射角变化范围为1°~80°。从图1中可以看出,同一频率下,水平极化时入射角越小,所引入的误差越大,垂直极化时入射角越大,所引入的误差越大。此外,还可以看出,入射角为20°~60°范围内,介电常数在反射系数中所引入的误差不到1dB。
表2具体给出了入射角为50°时,不同缩比因子时用淡水替代海水所引入的误差(原型为海水,频率为2GHz,入射角为50°)。从表2中可以看出,中等入射角的情况下,在满足可允许误差时,可以用淡水替代海水进行电磁缩比测量。
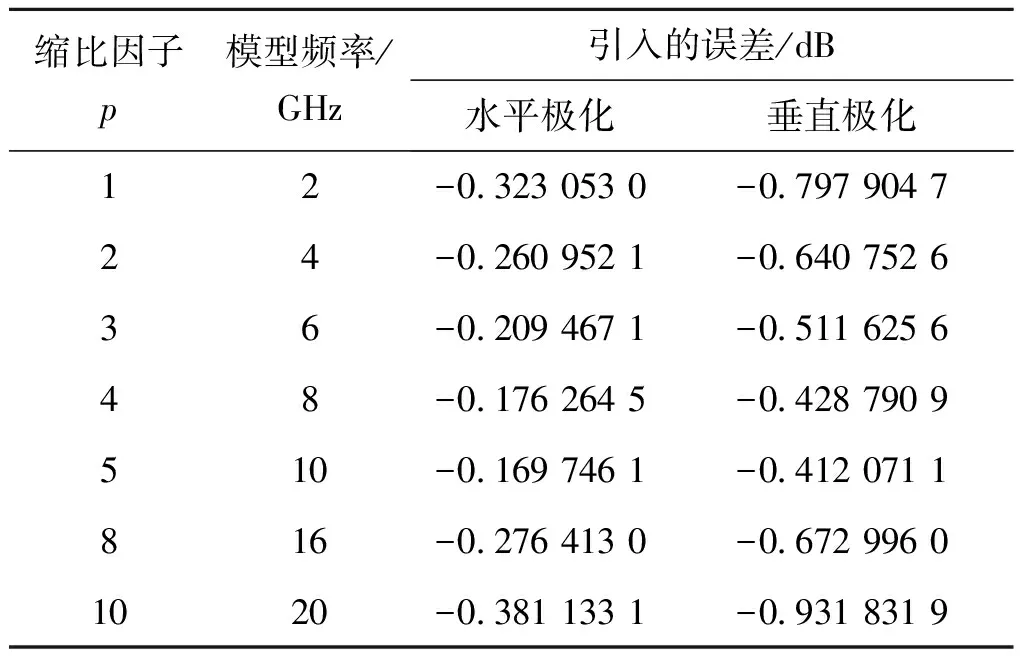
表2 入射角为50°时淡水替代海水所引入的误差
3 粗糙海面几何缩比关系
缩比模型与原型不仅要满足物理相似性,更重要的是几何上也要满足相似性,根据线性双叠加模型,海面高度可表示为[15]:
(8)
式中,M,N分别为频率和方向角的采样点数;ωmn、amn、φmn和ξmn分别表示组成波的圆频率、振幅、方向角和初始相位,km和kn是波数kmn沿x和y轴方向的分量。
若果原型海面和模型海面在几何上相似,则必须满足
(9)
式中,p为缩比因子。
根据假逆推的方法和各物理量的定义,可以得到
km′=kmp,kn′=knp
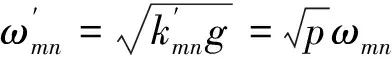
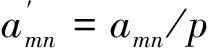
(10)
至此,式(9)和式(10)给出了模型和原型海面高度相关物理量之间的理论关系,即粗糙海面几何缩比条件,如表3所示。

表3 粗糙海面几何缩比条件
(11)
类似的,也可以得到二维JONSWAP海谱的几何缩比条件,如表4所示[14,17]。

表4 二维JONSWAP海谱几何缩比条件
为了验证粗糙海面的几何缩比条件,根据表3和表4所列的海面几何缩比条件,图2给出了不同缩比因子时原型海面和缩比模型海面的高度示意图。其中,原型粗糙海面的大小为Lx=Ly=256 m,Δx=Δy=1.0 m,海谱取JONSWAP谱,风速为U10=10 m/s,风向φw=0°。在实验室内模拟一个缩比海面,水深通常是有限的,因此在色散关系中考虑水深是比较切合实际的,角频率ω与波数k满足的色散关系如下:
(12)
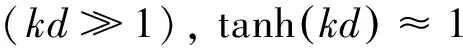

4 数值仿真
理论上,如果原型和缩比模型两个电磁系统是相似的,则其散射系数是一致的。根据海面面元散射模型[18],图3给出了原型海面和缩比模型海面的单双站散射系数。其中,原型系统的入射频率为2GHz,离散数目为M=N=256,离散间隔为Δx=Δy=1.0m,风速U10=10m/s,风向φw=0°,原型海水的盐度和温度为S=35ppt,T=20 ℃;缩比模型为淡水,即S=0,T=20 ℃,且模型的水深为d=2m。对于双站散射,入射方向为θi=40°,φi=0°,散射方向为φs=0°。
从图3可以看出,缩比模型海面和原型海面的后向散射系数在小角度时吻合的比较好,随着入射角的增大,它们之间的误差越大,这是由于淡水替代海水所引入的误差越大(从图1中淡水替代海水在反射系数中体现出来的误差可以明显地观察到)。对于双站情况,在镜向和前向,缩比模型海面和原型海面的散射系数吻合的比较好,此外,HH极化时,缩比模型海面的散射系数与原型海面的散射系数的差异比VV极化时的要小。
图4对比了HH极化时原型海面和缩比模型海面的散射场模值的空间分布。其中,入射角为θi=50°,其他参数同上。从图4中可以看出,缩比模型海面的散射场模值的空间分布与原型海面的基本一致。
上面分析了电磁缩比条件对于静态海面的适用性,为了分析海面的动态特性,图5给出了HH极化下缩比模型海面和原型海面的后向杂波序列,其中,入射角为θi=50°,时间步dt=0.01 s,时间采样点数为1 024。图6给出了缩比模型海面和原型海面的平均多普勒谱。其中,入射角为θi=50°,时间步dt=0.01 s,时间采样点数为128。多普勒谱是对50个粗糙海面进行平均,其他参数也同上。
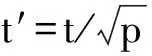
5 结论
本文提出了海面电磁散射测量的替代模型。该模型采用淡水替代海水进行海面缩比测量,可以避免实验室内采用海水测量时缩比条件要求的理论温度和盐度的不可实现性和海水对造波设备的腐蚀。数值仿真表明,中等入射角下,采用淡水替代海水进行海面缩比测量在反射系数中所引入的误差不到1 dB。此外,缩比模型和原型海面之间的单双站散射系数、散射场模值的空间分布、杂波序列及多普勒谱的比较也表明,在实验室内用淡水替代海水进行海面缩比测量具有一定的可行性。
[1]Blacksmith P J, Hiatt R E , Mack R B. Introduction toradar cross-section measurements [J]. Proc. IEEE, 1965, 53(8): 901-920.
[2]Stratton J A. Electromagnetic theory [M]. McGraw-Hill Book Co. N.Y., 1941.
[3]Sinclair G. Theory ofmodels of electromagnetic systems [J]. Proc. IRE, 1948, 36(11): 1364-1370.
[4]Sinclair G. Measurement of aircraft-antenna patterns using models[J]. Proc. IRE, 1947, 35(12): 1451-1462.
[5]Bachman C G. Some recent developments in RCS measurement techniques [J]. Proc. IEEE, 1965, 53(8): 926-927.
[6]Daniel A Saylor, D Brett Beasley. Current status of IR scene projection at the U S Army Aviation and Missile Command[C]//Proceedings of SPIE. US:SPIE, 2001: 147-157.
[7]杨俊杰. 相似理论与结构模型试验[M]. 武汉: 武汉理工大学出版社, 2005: 21-27.
[8]周美立. 相似工程学[M]. 北京: 机械工业出版社, 1998: 164-165.
[9]Trizna D B. A model for Brewster angle damping and multipath effects on the microwave radar sea echo at low grazing angles [J]. IEEE Transactions on Geoscience and Remote Sensing,1997, 35(9): 1232-1244.
[10]Martin G, Nicole B. Laboratory measurements of artificial rain impinging on a wind-roughened water surface [J]. IEEE International Geoscience and Remote Sensing Symposium Proceedings, 1998(5): 2559-2561.
[11]Jerry R Smith, Steven J Russell, Barry E Brown, et al.Electromagnetic forward-scattering measurements over a known, controlled sea surface at grazing [J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(6): 1197-1207.
[12]岳慧, 王晓冰, 薛正国. 粗糙海面的电磁散射缩比模拟测量的若干基本问题[J]. 制导与引信, 2010, 31(4): 30-34.
[13]Klein L A, Swift C T. An improved model for the dielectric constant of sea water at microwave frequencies [J]. IEEE Trans. Antennas Propagat., 1977, AP-25(1): 104-111.
[14]Zhao Y, Zhang M, Chen H. The EM scattering of electrically large dielectric rough sea surface at 240 GHz using a scale model [J]. IEEE Transactions on Antennas and Propagation, 2012, 60(12): 5890-5899.
[15]Dalrymple R A, Rogers B D. Numerical modeling of water with the SPH method [J]. Coastal Engineering, 2006, 53(2): 141-147.
[16]Claus B, Werner A, Klaus H. Monte-Carlo simulation studies of the nonlinear imaging of a two dimensional surface wave field by a synthetic aperture radar[J]. Int. J. Remote Sensing, 1990, 11(10): 1695-1727.
[17]张民, 郭立新, 聂丁, 等. 海面目标雷达散射特性与电磁成像[M]. 北京:科学出版社, 2015.
[18]Zhang M, Chen H, Yin H C. Facet-based investigation on EM scattering from electrically large sea surface with two-scale profiles: theoretical model [J]. IEEE Trans. Geosci. Remote Sens., 2011, 49(7): 1967-1975.
Alternative Model of EM Scale Measurement of Sea Surface
ZHAO Ye1, ZHANG Danmeng2, CAO Yi3
(1.School of Physics and Electronic Information, Yanan University, Yan’an 716000, China; 2.College of Electrical Engineering and Automation, Anhui University, Hefei 230601, China; 3.Xi’an Institute of Electromechanical Information Technology, Xi’an 710065, China)
the sea surface scale measurement need to measure the dielectric constant temperature and salinity of seawater. An alternative model of electromagnetic (EM) scale measurement for sea surface was presented. The proposed model used freshwater instead of seawater to do the scaling measurement, which could avoid the impossibility of the theoretical temperature and salinity in the laboratory and the corrosion of seawater to the wave generators. Numerical simulations showed that the resulted error in the reflection coefficient at moderate incident angle was no more than 1 dB when using the freshwater in the scaling measurement. Moreover, the comparisons of the scattering coefficient, spatial distribution of scattering field, clutter time series and Doppler spectrum between the scale model and prototype also showed that the alternative model of EM scale measurement for sea surface was feasible in some degree.
sea surface; dielectric constant of sea water; scale model; scattering coefficient
2017-01-21
延安大学博士科研启动项目资助(YDBK2016-16)
赵晔(1987—),女,陕西子长人,博士,研究方向:复杂目标与环境的电磁散射建模与电磁成像。E-mail:zhaoye07074135@163.com。
TN011
A
1008-1194(2017)03-0024-06

