基于分块对角矩阵的二维压缩感知数据采集和重构方法

程 涛

(1.深圳大学光电子器件与系统重点实验室，广东 深圳 518060； 2.广西科技大学汽车与交通学院，广西 柳州 545006； 3.深圳生物医学光学微纳检测与成像重点实验室，广东 深圳 518060)

基于分块对角矩阵的二维压缩感知数据采集和重构方法

程 涛1,2,3

(1.深圳大学光电子器件与系统重点实验室，广东 深圳 518060； 2.广西科技大学汽车与交通学院，广西 柳州 545006； 3.深圳生物医学光学微纳检测与成像重点实验室，广东 深圳 518060)

针对遥感中线阵推扫数据采集模式和现有方法重构能力的不足，提出基于分块对角矩阵和TV (Total Variation)算法的二维压缩感知模型和方法。该方法能够使压缩感知的约束函数和目标函数同时包含完整的图像二维信息，是真正完全意义上的二维压缩感知。在不改变传统数据采集模式的基础上，通过分块对角矩阵的后处理，实现二维压缩感知。实验结果表明，该方法使图像的重构效果获得极大改善，SNR提高约8 dB。但是该方法不适用于OMP(Orthogonal Matching Pursuit)和BP(Basis Pursuit)算法。该方法促进了定向遥感的发展，如与其他模型和方法结合，能进一步提高重构效果。

二维压缩感知；定向遥感；线阵推扫；分块对角矩阵；全变分

0 引言

根据奈奎斯特采样定理， 采样频率是信号最高频率2倍以上时，才能确保由采样完全重构原始信号。压缩感知能以远低于奈奎斯特采样定理要求的频率采样，在采集信号的同时实现对信号的压缩，并能高质量地恢复原始信号[1-2]。因此，压缩感知一出现就在图像处理、视频分析、雷达遥感、信息通信和医学成像等领域成为研究热点[3-4]。但是当前研究多是将压缩感知作为一种数据后处理技术。真正能将压缩感知应用于数据采集领域也只有CT(Computed Tomography，即电子计算机断层扫描)和MRI(Magnetic Resonance Imaging，磁共振成像)等医学成像和超分辨显微成像等几个能够实现凝视状态的领域[5-7]。

遥感数据的获取一般分为星上和地面两个阶段。在卫星上需要采集、压缩和传输数据，在地面需要接收、储存、解压和使用数据。遥感技术的发展使覆盖全球海量遥感数据的获取成为现实。如能实现采集压缩一体化的信号数据采集处理格局，就可采集、传输、存储、处理和管理很少的数据，从而摆脱传统技术的窘境，节约巨大的人力物力资源。压缩感知技术的出现为改变传统的遥感数据获取模式提供了可能。文献[8-9]基于线阵推扫模式提出定向遥感和定向变化检测。一般，采集2～3倍的测量数据就可完全重构变化区域。但是当前的各种压缩感知重构算法和模型无法在线阵推扫模式下充分利用已有的先验信息，因此重构效果并不好。本文针对当前遥感中基于线阵推扫模式的数据采集方法不能充分利用信号先验信息的不足，提出了基于分块对角矩阵和TV算法的二维压缩感知模型和方法。

1 压缩感知理论

压缩感知理论表明，如果信号是稀疏或可压缩的，就能以远低于奈奎斯特(Nyquist)采样定理的采样率采集信号，并能以高概率精确或近似重建信号，压缩感知模型如式(1)所示，求解式(1)就可以重构出信号x[10-11]。

min‖x‖0s.t.y=Φx

(1)

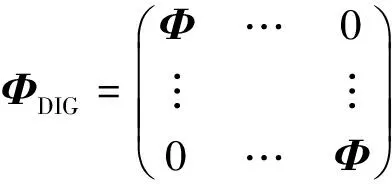
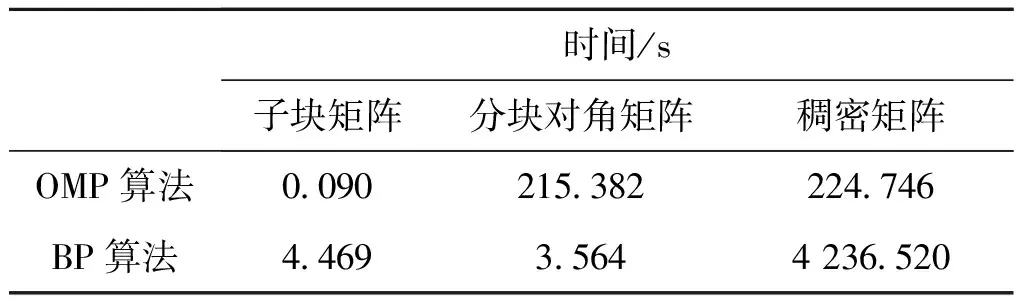
式中，y是测量数据，y∈RM；Φ是测量矩阵，Φ∈RM×N，M

测量矩阵Φ的性质是关系信号重构效果的关键。当前判断测量矩阵Φ性能优劣的主要判据为是否满足RIP(Restricted Isometry Property，约束等距性质)，如式(2)所示[10-11]。随机矩阵的RIP性质一般都较好。

(1-σK)‖x‖2≤‖Φx‖2≤(1+σK)‖x‖2

(2)

式中，σK∈[0,1)。

如果测量矩阵满足RIP和Johnson- Lindenstrauss定理，那么可导出RCP(Restricted Conformal Property，约束保角性质)，如式(3)所示[12]：

(3)

RIP主要反映了测量数据和信号之间的能量继承关系，RCP反映了测量数据和信号之间的方向继承关系。在二维情况下，这种继承关系表现的非常明显，并可作为判断能量和方向的先验信息[8-9,13]。

2 基于线阵推扫模式的二维压缩感知

当前基于压缩感知的遥感研究多是基于一维信号。即使研究图像这种二维信号也多是转化为一维信号后再作压缩感知研究。在压缩感知的各种重构算法中，只有最小全变分法(Total Variation，TV)在目标函数中利用了图像像素间的灰度梯度信息，但在约束函数中依然把二维信号一维化。从重构效果看，只有在梯度大的地方优于离散余弦变换(Discrete Cosine Transform, DCT)。灰度梯度就是遥感影像的结构之一，是很好的先验信息，如充分利用可有助于改善提高信号的重构精度和效率。但把二维图像一维化破坏了这种结构先验信息[8,14]。

遥感卫星等的影获取多是采用线阵推扫模式，设扫描条带的长度为L。如果以矩阵X(X∈RN×L)表示扫描条带，则卫星或飞机的扫描线每次只能取得X某列的数据。以二维形式表示其压缩感知模型，则如式(4)所示：

min‖xj‖0s.t.Y=ΦX,j∈[1,L]

(4)

式中，Y∈RM×L，xj是X的列向量。由式(4)可见，二维化后的测量矩阵Φ的规模为M×N；如果将遥感影像转化为一维信号，测量矩阵Φ的规模为ML×NL，前者仅为后者的1/L2。测量矩阵规模的缩小将会大大提高数据解算的速度和效率。式(4)也可等价表示成式(5)，两种表示方法并无本质区别，因此式(4)并不是完全意义上的二维压缩感知模型。但是式(4)的约束函数能更好地反映信号和测量数据的二维信息[8]。

min‖xj‖0s.t.yj=Φxj

(5)

文献[13]基于式(5)采用OMP算法逐列重构，然后通过RCP，利用二维图像的列间相关性，对重构结果修正，取得了更好的重构效果。对于可压缩信号，TV是效果最好的重构算法。文献[9]对满足稀疏要求的列采用OMP算法重构，然后利用RCP先验信息确定出可压缩列，并对之采用TV重构，取得了很好的重构效果。这些方法在压缩感知模型的目标函数中并没有引入列间的相关性信息，而是通过后处理的形式判断重构结果的优劣，并对重构不好的区域修正。因此本质上都不是真正的二维压缩感知。

min‖X‖TVs.t.Y=ΦX

(6)

如能将式(4)转化为式(6)的形式就能实现真正的二维压缩感知。因为式(6)的目标函数既包含了图像纵向(列向)的灰度梯度信息，也包含了图像横向的灰度梯度信息。约束函数也完整保留了图像和测量数据的二维结构信息。

但是式(6)并不能直接应用于现有压缩感知的TV模型。因此，如将式(6)中的图像，测量数据都一维化，那么式(6)就等价转化为式(7)。式(6)和式(7)的目标函数尽管写法不一样，但本质上是完全等价的，都包含了图像横向和纵向的全部梯度信息；约束函数在数学上也是完全等价的，并没有导致信息的丢失和减少。

min‖x‖TVs.t.y=ΦDIGx

(7)

3 实验结果分析和验证

所有的实验采用Matlab在普通台式机上完成，CPU主频3.1 GHz，4核，内存1 GB。Matlab的操作界面如图2所示。用灰度图表示的子块矩阵Φ、分块对角矩阵ΦDIG和稠密矩阵ΦDEN如图3所示。子块矩阵Φ的矩阵规模为M×N；分块对角矩阵ΦDIG的矩阵规模为ML×NL，其中包含L个子块矩阵Φ；稠密矩阵ΦDEN的矩阵规模为ML×NL，其大小是子块矩阵Φ的L2倍。子块矩阵Φ和稠密矩阵ΦDEN都是服从N(0，1/M)分布的高斯测量矩阵，两者的区别只在于矩阵大小规模的不同。

基于子块矩阵Φ的重构算法流程，就是通过Φxj逐列采集测量数据yj；然后，基于式(5)，通过TV算法逐列重构xj；最后，将逐列重构得到的所有xj，排列组合成二维图像X。

基于分块对角矩阵ΦDIG的重构算法流程，就是通过如图1所示的算法流程图重构得到二维图像X。

基于稠密矩阵ΦDEN的重构算法流程，就是通过稠密矩阵ΦDEN直接采集二维图像X的一维化数据x，ΦDENx；然后，基于min‖x‖0s.t.y=ΦDENx，通过TV算法重构得到x；最后将x二维化成二维图像X。

图4和表1是基于子块矩阵Φ、分块对角矩阵ΦDIG和稠密矩阵ΦDEN对Boats、Cameraman、Lena和遥感影像Mulargia lake以及墨西哥森林5幅图像采用TV算法的重构结果。Mulargia lake是意大利撒丁岛Mulargia湖的两个时相遥感影像的差值图，由Landsat-5卫星在波段4分别拍摄于1995年09月和1996年07月。该图像反映了Mulargia湖水位上升而造成的陆地淹没情况。为满足定向遥感的稀疏条件，对两个时相的原始遥感影像做简单处理，使其差值图中未变化区域的灰度值都为0。墨西哥森林是拍摄于某时刻的遥感图像，背景与目标灰度非常相近，几乎无法区分目标和背景。图4中，除Mulargia Lake外的其他4幅图都是可压缩的。Mulargia Lake图中的黑色区域的像素灰度都为0。除此之外的其他区域也是可压缩的。表1中，包含横向灰度梯度信息的目标函数值用TV表示，横向灰度梯度信息用TVx表示，TV和TVx的值×104后才是其真实值。

子块矩阵基于式(5)逐列重构，分块对角矩阵基于式(7)重构。稠密矩阵也基于式(7)重构，不过这时式(7)中的约束函数的分块对角矩阵用稠密矩阵替换。子块矩阵和稠密矩阵都是高斯矩阵。

图4中自左向右依次是基于子块矩阵、分块对角矩阵和稠密矩阵的重构结果，最右侧是原始图像。对比左侧的两列图像可以发现，基于TV算法的分块对角矩阵的重构效果远远好于子块矩阵逐列重构的效果。由表1可见，前4幅图的SNR提高约8 dB，计算时间最大约增加22倍(通过Matlab中的tic和toc命令统计计算时间)。而对于背景与目标灰度非常相近的墨西哥森林，SNR仅提高约2.5 dB，计算时间约增加14倍。包含横向灰度梯度信息的最终目标函数数值(TV)和横向灰度梯度值(TVx)都小于子块矩阵，更接近于稠密矩阵。

SNR计算公式如式(8)所示：

(8)

式中，x是真实信号，x∈RN；‖·‖2表示向量的模；xR表示x的重构结果。

对比左侧的两幅Lena图可以发现，Lena图中左侧立柱的重构效果，分块对角矩阵劣于子块矩阵。这说明，逐列重构的子块矩阵更适用于灰度梯度纵向变化平缓的图像局部区域。对比左侧的两幅Cameraman图可以发现，在头部附近的纵向区域，逐列重构的子块矩阵的重构效果也劣于分块对角矩，这是因为该区域的纵向灰度梯度变化大。分块对角矩阵更适用于灰度梯度横向变化平缓的图像局部区域；例如，Boats图的横向灰度梯度变化较小，纵向灰度梯度变化大，所以子块矩阵逐列重构得到的左侧Boats图的所有区域都很模糊。

表1 3类矩阵的SNR和计算时间

如果将逐列重构的子块矩阵和分块对角矩阵相结合，在纵向灰度梯度变化平缓的区域采用逐列重构的子块矩阵，在其他区域使用分块对角矩阵就能取得更好的重构效果。

由图4和表1可见，稠密矩阵的重构效果和SNR尽管都好于分块对角矩阵，但是稠密矩阵这种矩阵形式并不能应用于基于线阵推扫的遥感数据采集模式中。由表1可见，分块对角矩阵和稠密矩阵的计算速度几乎相当，远远慢于子块矩阵。这是因为子块矩阵的矩阵规模远远小于分块对角矩阵和稠密矩阵。

由于在TV算法中， 3类矩阵的目标函数包含信息量的不同，导致无法准确测试3类矩阵的性能和效果，因此，基于OMP和BP算法测试3类矩阵的性能。基于不同稀疏度的高斯信号，各实验64次，计算精确重构概率。图5和表2是基于子块矩阵、分块对角矩阵和稠密矩阵对同一套测试数据分别采用OMP和BP算法的重构结果。由图5中OMP和BP可见，稠密矩阵在稀疏度较小时重构效果好于子块矩阵；当稀疏度较大时反之；分块对角矩阵的重构效果最差。

由表2可见，OMP算法，子块矩阵的计算速度最快。分块对角矩阵和稠密矩阵的计算速度相近，都远远慢于子块矩阵。BP算法，稠密矩阵的计算速度最慢。子块矩阵和分块对角矩阵的计算速度相近，都远远快于稠密矩阵。

时间/s子块矩阵分块对角矩阵稠密矩阵OMP算法0 090215 382224 746BP算法4 4693 5644236 520

在TV算法中，分块对角矩阵和稠密矩阵的目标函数不但包含原始图像的纵向灰度梯度信息，而且还包含横向的灰度梯度信息；但是子块矩阵只包含原始图像的纵向灰度梯度信息。OMP和BP算法表明，分块对角矩阵性能劣于子块矩阵和稠密矩阵。但是在TV算法中，包含横向灰度梯度信息的目标函数弥补，并远远超过了分块对角矩阵性能的不足。

文献[9]说明TV算法只适用于可压缩信号，对于稀疏信号，使用其他算法可取的更好的重构效果。因此，在定向遥感的实际使用中，对稀疏区域使用其他重构算法重构，对于可压缩区域中纵向灰度梯度变化平缓的使用逐列重构的子块矩阵；对于可压缩区域中纵向灰度梯度变化不平缓区域的使用分块对角矩阵重构。

4 结论

本文提出了基于分块对角矩阵和TV算法的二维压缩感知模型和方法。该方法能够使压缩感知的约束函数和目标函数同时包含完整的图像二维信息，是真正完全意义上的二维压缩感知。实验结果表明，由于目标函数中包含了图像的二维梯度信息，该方法使图像的重构效果获得极大改善，SNR提高约8 dB，但是该方法不适用于OMP和BP算法。这是因为它们的目标函数中并不包含图像的二维梯度信息，本质上依然是一维压缩感知。利用更多图像像素相关信息的目标函数能改善重构效果。该方法促进了定向遥感的发展，拟结合其他模型和方法，进一步提高重构效果。

[1]CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. Information Theory, IEEE Transactions on, 2006, 52(2): 489-509.

[2]CANDES E J, TAO T. Decoding by linear programming [J]. Information Theory, IEEE Transactions on, 2005, 51(12): 4203-4215.

[3]焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望 [J]. 电子学报, 2011, 39(7): 1651-1662.

[4]林杰, 石光明, 董伟生. 基于信息自由度采样的信号重构方法研究进展 [J]. 电子学报, 2012, 40(8): 1640-1649.

[5]ZHU L, ZHANG W, ELNATAN D, et al. Faster STORM using compressed sensing [J]. Nature methods, 2012, 9(7): 721-723.

[6]DONOHO D L. Compressed sensing [J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[8]程涛, 朱国宾, 刘玉安. 基于二维压缩感知的定向遥感和变化检测研究 [J]. 红外与毫米波学报, 2013, 32(5): 491-496.

[9]CHENG T. Directional Remote Sensing [J]. Geod list, 2015, 52(4): 251-262.

[10]DONOHO D L. Compressed sensing [J]. Information Theory, IEEE Transactions on, 2006, 52(4): 1289-1306.

[11]CANDES E J. Compressive sampling [C]//Proceedings of the International Congress of Mathematicians. Madrid, Spain: European Mathematical Society, 2006: 1-20.

[12]CHENG T. Restricted Conformal Property of Compressive Sensing [C]//2014 11th International Conference on Wavelet Active Media Technology and Information Processing. Chengdu: UESTC Press, 2014: 152-161.

[13]程涛, 朱国宾, 李小龙. 基于信号方向信息的二维压缩感知影像重构研究 [J]. 半导体光电, 2014, 35(4): 32-37.

[14]程涛. 基于压缩感知的遥感变化检测研究 [D]. 武汉: 武汉大学, 2013.

Two-dimensional Compressive Sensing Data Acquisition and Reconstruction Based on Block Diagonal Matrix

CHENG Tao1,2,3

(1.Key Laboratory of Optoelectronic Devices and Systems, Shenzhen University, Shenzhen 518060, China; 2.Automotive & Transportation Engineering Institute，Guangxi University of Science and Technology, Liuzhou 545006, China; 3.Shenzhen Key Laboratory of Micro-Nano Measuring and Imaging in Biomedical Optics, Shenzhen University, Shenzhen, 518060, China)

For the data acquisition modes of linear array push-broom in remote sensing and deficiencies of existing methods for data reconstruction, the two-dimensional compressive sensing models and methods based on a block diagonal matrix and TV (Total Variation) algorithm were proposed in this paper. This method enabled the constraint and objective functions of compressive sensing to contain the completed two-dimensional image information. And it was totally real two-dimensional compressive sensing. On the basis of the traditional data acquisition mode, the two dimensional compressive sensing was realized by the post processing of the block diagonal matrix. Experimental results showed that the image reconstruction effect was improved greatly, and the SNR increased by about 8dB. However, this method was not suitable for OMP (Orthogonal Matching Pursuit) and BP (Basis Pursuit).

two-dimensional compressive sensing; directional remote sensing; linear array push-broom; block diagonal matrix; TV(total variation)

2017-01-10

国家自然科学基金项目资助(41461082,81660296); 中国博士后科学基金项目资助(2016M592525);广西自然科学基金项目资助(2014GXNSFAA118285);广西高校科学技术研究项目资助(YB2014212);广西科技大学博士基金项目资助(校科博13Z12)

程涛(1976—)，男，广西柳州人，博士，副教授，研究方向：压缩感知和遥感研究。E-mail:ctnp@163.com。

TP391

A

1008-1194(2017)03-0060-06