一种分层信息提取的多块主元分析故障监测方法

翟 超,熊伟丽

(江南大学 轻工过程先进控制教育部重点实验室,江苏 无锡 214122)

随着传感和检测技术飞速发展,工业生产的信息化程度不断提高,产生了大量的生产过程数据,因而多元统计过程监控(MSPM)方法得到了广泛应用。其中主元分析(Principal component analysis,PCA)、偏最小二乘(Plus least square,PLS)和独立元分析(Independent component analysis,ICA)等是比较经典的多元统计监控方法[1-3]。针对工业过程呈现的不同特征,研究者们对3种经典方法进行了一系列改进[4-9]。其中,Nguyen等[6]提出了使用核技巧计算非线性主元的核主元分析法(Key PCA,KPCA),无需考虑非线性优化问题,具有更加优越的性能。针对PCA不能解决非高斯过程监测的问题,Ge等[7]提出了一种基于独立元分析-主元分析(ICA-PCA)的故障监测方法,通过提取过程的高斯和非高斯信息用于故障检测和诊断。Zhou等[8]提出一种全潜投影偏最小二乘方法,对PLS的主元及残差空间进行了二次分解,质量相关故障和无关故障的监测性能在一定程度上同时得到了提升。然而这些方法都是建立一个全局模型,没有考虑到生产过程中的局部信息,容易忽略局部产生的故障。

在现代工业中,以大规模和多个操作单元为特征的生产过程越来越多。而当这样的生产过程发生故障时,可能只有部分变量受到影响,这时若只建立全局模型,那么局部信息可能会被淹没,因此,多块或分布式过程监控成为一种有效的解决方案。国内外学者已经提出多种多块监控方法来获得复杂过程变量之间的关系,并能够反映过程的局部特性[10-15]。Macgregor等[12]提出了多块投影方法,为每个子块以及整个过程建立监控图表。Westerhuis等[13]从算法角度比较了传统PCA和PLS方法,先根据已有知识对变量进行分块,再用其分别对子块建模,最后将结果融合。这些分块方法要求熟悉工业过程并具备一定的先验知识,当先验知识相对匮乏时,模型建立变得十分困难。因此基于数据的变量分块方法成为了研究热点。一种基于故障的变量选择和基于贝叶斯推断的分布式方法由Jiang等[14]提出,首先使用优化算法为每个故障识别最佳变量子集,其次对每个子块进行PCA监测模型的建立,最后通过贝叶斯推断来融合所有子集的监测结果。Huang等[15]考虑过程的高斯特性,对过程分块,分别用DPCA和DICA 方法对相应子块进行监控。

上述多块监测方法在分析各过程变量之间关系的基础上,通过构建一些规则将变量分块,取得了优于单一模型的监测效果,但是仅使用了过程数据的观测值,并没有挖掘隐含在数据中的其他有效信息。顾炳斌等[16]提出了一种新的分块思想,同时提取过程数据观测值、累计误差和变化率信息,将原始数据集扩充为3个子块分别监测,最终将子块的监测结果融合,利用了数据中隐含的信息使得监测效果有所提升。

为了在考虑过程局部信息的同时,挖掘并利用数据集中的其他特征信息,提出一种分层信息提取的多块PCA故障监测方法。首先通过计算变量之间的互信息值对过程变量进行分块,提取局部信息;其次对分块后的变量块进一步提取累计误差和二阶差分等信息,将变量块扩充为多个信息子块,使得子块同时包含过程的局部信息和数据集的特征信息;再对每个信息子块采用PCA方法进行建模并监控,最后将所有子块的监测结果进行贝叶斯融合输出。在TE过程的仿真实验中,验证了所提方法优于传统监测方法,提升了监测性能。

1 PCA故障监测原理

PCA作为一种降维方法,在保留工业过程主要信息的同时,将高维的过程数据投影至正交的低维子空间,目前在故障监控领域得到了广泛应用[1]。假设过程变量数据矩阵为X∈Rn×m,对其标准化预处理后进行主元分析可得

X=TPT+E

(1)

式中:T∈Rn×k为得分矩阵,P∈Rm×k为载荷矩阵,E∈Rn×m为残差矩阵。

利用PCA进行过程监测时,分别在主元空间和残差空间中构造T2和SPE统计量,根据其是否超限来判断过程是否发生故障。假设一个新的测试样本为x∈Rm×1,在PCA监测模型中其T2和SPE统计量分别为

(2)

SPE=xT(I-PPT)x≤SPElim

(3)

2 基于分层信息提取的分块方法

传统的多块建模方法依靠对过程变量进行选择来对过程分块,从而获得生产过程的局部信息。本文考虑到信息的多样性,在变量分块后,进一步对每个变量块提取累计误差和二阶差分等信息,挖掘原始数据集中的隐含信息,将每个变量块进一步扩充为同时包含局部信息和特征信息的信息子块,再对所有子块进行分块监测。分层信息提取的多块建模方法与传统多块建模方法对比如图1所示。

2.1 局部信息提取

本文通过计算变量之间的互信息值对过程变量进行分块,以提取过程的局部信息。互信息是信息论中的概念,用于判断一个随机变量与另一个随机变量之间重叠信息量的大小,也能用于衡量两个变量之间的相关程度。两个变量之间互信息值的大小决定其相关性的强弱[17-19]。互信息的计算公式为

(4)

式中:p(x,y)为两个变量x和y的联合概率密度,p(x)和p(y)为两个变量的边缘概率密度。

考虑到概率密度函数的获取难度较大,所以一般情况下互信息可由式(5)计算。

I(x,y)=H(x)+H(y)-H(x,y)

(5)

式中:H(x)和H(y)分别为变量x和y的边缘熵,H(x,y)为两个变量的联合熵,其计算公式为

(6)

(7)

(8)

假设原始数据集为X∈Rn×m,m为变量个数。通过计算各变量之间互信息值大小,对m个过程变量进行分块,提取过程局部信息,将原始数据集分为b个子块,即X=[X1,X2,…,Xb]∈Rn×m。

2.2 特征信息提取

2.2.1 累计误差信息

累计误差信息是通过计算一定时间段内累计的观测值信息与预设标准值的差所得到的信息。故障发生时,若过程变量表现出微小的变化以及缓慢的偏移,过程的累计误差信息可以在一定程度上放大这种变化或偏移,使得这类故障更容易被监测到,从而提升监测效果[16]。

假设标准化后的过程变量数据集经过变量选择分块后的某一变量块为Xb∈Rn×b,其均值为0。将标准值设定为变量的均值,那么将样本值相加即可得到累计误差信息。将前T个时刻的累计误差信息作为新的特征信息,构造新的特征信息子块Xbl∈R(n-T)×b。第t个时刻的累计误差为

(9)

式中:xl(t)表示t时刻的累计误差信息,x(t)为该变量块中t时刻的样本。由于原始数据中前T个样本用来构造新的特征,因此新的特征数据集会损失T个样本。

2.2.2 二阶差分信息

二阶差分是指在数据进行一次差分的基础上,对差分后的数据再进行差分,可以进一步反映过程的动态特征。当某个或某些故障导致相关变量产生振荡而不单单是幅值变化时,观测值信息和累计误差信息均无法很好地对故障进行监测。而对数据进行二阶差分后,能够有效地观测到此类故障,通过提取该信息用于建模,能够更好地对此类故障进行监测。

假设标准化后的过程变量数据集经过变量选择分块后的某一变量块为Xb∈Rn×b,通过对每个时刻变量求取二阶差分构造新的特征信息子块Xbd∈R(n-2)×b,t时刻的二阶差分信息为

xd(t)=(x(t)-x(t-1))-(x(t-1)-x(t-2))

(10)

式中:xd(t)为t时刻的二阶差分信息,x(t)为该变量块中t时刻的样本。

通过对变量子块提取累计误差及二阶差分信息,得到信息子块Xbl和Xbd,结合原始数据观测值信息Xb,将每个变量块扩充为3个信息子块,每个信息子块包含了过程的局部信息和数据集的特征信息。

3 分层信息提取的多块PCA故障在线监测

3.1 故障监测的主要步骤

首先,计算各个变量之间的互信息值,通过互信息值对变量进行分块,以提取过程局部信息。

其次,对利用互信息值划分的各个子块,提取其累计误差信息和二阶差分信息,与原始数据观测值信息共同将每个变量子块扩充为3个特征信息子块。

进一步,采用PCA方法对所得的信息子块进行故障监测,得到各个信息块的统计量与控制限。

最后,为了得到一个直观的监测指标,基于贝叶斯推断,对所有子块的监测结果进行融合,并将结果作为最终的统计监测指标。

对于一个测试样本xtest,在贝叶斯方法中,其在第i个子块中T2统计量故障的条件概率为

(11)

PT2(xtest,i)=PT2(xtest,i|N)PT2(N)+

PT2(xtest,i|F)PT2(F)

(12)

条件概率PT2(xtest,i|N)和PT2(xtest,i|F)定义分别为

(13)

(14)

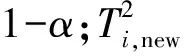
(15)

同理,经过BIC融合后的SPE统计量可由式(16)计算。

(16)

3.2 故障监测算法流程

分层信息提取的多块PCA(Hierarchical information extraction PCA,HIEPCA)故障监测方法的流程如图2所示,以下对算法具体实施过程进行详细描述。

(1)对正常数据集X0进行标准化处理,获得数据集X。

(2)计算数据集中变量之间的互信息值,并根据互信息值的大小对变量进行分块,生成b个变量子块。

(3)对分类过后的每个变量子块分别提取累计误差信息和二阶差分信息,与原始数据信息共同组成新的信息子块,最终生成3×b个信息子块。

(4)对生成的所有信息子块中建立PCA模型,并计算子块的故障控制限。

(5)对于新的测试样本,经过标准化处理后按照步骤2和3中的方法得到新的测试样本。

(6)对每个信息子块进行监测,得到各信息子块的监测结果。

(7)对各子块的监测结果采用贝叶斯方法,得到BIC统计量,作为最终的监测结果。

4 仿真实验

4.1 TE过程介绍

TE仿真过程由伊斯曼化学公司创建,旨在提供一个基于工业过程的真实测试平台用以评估过程控制和监控性能。该过程包括5个主体部分:反应器、冷凝器、压缩机、分离器和汽提塔[21]。整个过程共包含53个变量,其中有22个测量变量,12个操作变量,以及19个成分变量,TE过程的详细描述可参考文献[22],本文选取测量变量和操作变量(除去搅拌速度外)用于建模和监测。TE过程设定的不同故障共有21中,包括16种已知故障和5种未知故障。分别采集正常工况下和各种故障工况下的960个样本作为训练和故障测试集,故障样本中的故障均从第161个点开始产生。

4.2 仿真结果分析

图3展示了33个变量之间的互信息值,不同颜色对应其大小(范围为0～1)。大多数变量之间的互信息值不超过0.2,因此,本文将0.2作为互信息阈值。若两个变量之间互信息值超过阈值,当故障发生时,其受到的影响相似,将其分入一个子块将更容易检测到故障。例如变量12和29的互信息值达到0.996 6,变量15和30的互信息值为0.996 3,则将变量12和29分为一块,同理将变量15和30分为一块。将与其他所有变量之间互信息值均小于阈值0.2的变量分入一个子块中进行监测,共将33个过程变量分为8个子块。具体的变量分块结果如表1所示。

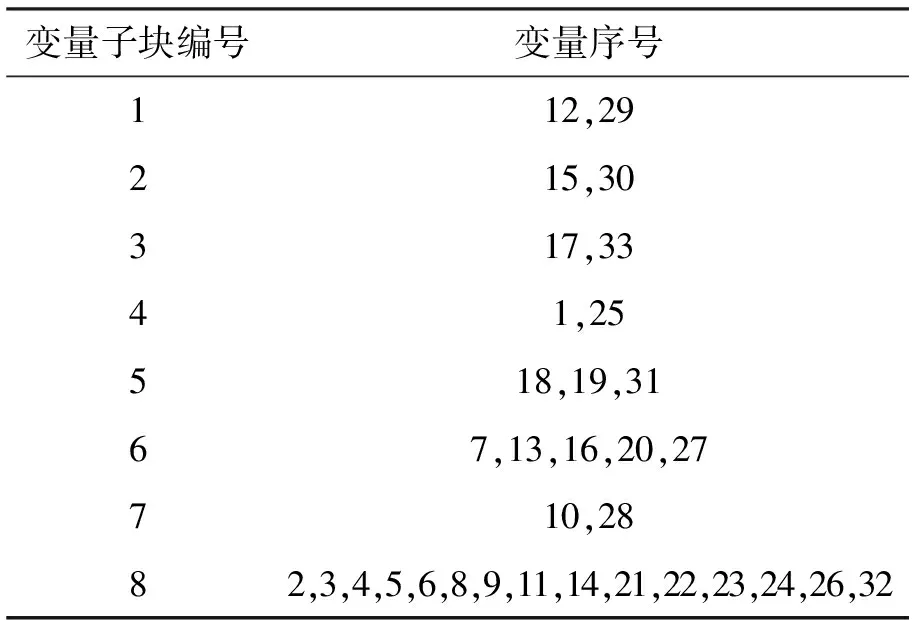
表1 变量分块结果

对于经过第一层信息提取后的变量子块,以第一个变量子块X1∈R960×2为例(包含变量12、29),进行特征信息提取。首先计算前T个时刻的累计误差信息,仿真中取T=5,构造累计误差特征信息子块X1l∈R955×2;然后根据二阶差分信息计算方法可得特征信息子块X1d∈R958×2;观测值信息即为变量子块数据X1∈R960×2。由于累计误差信息宽度T取值为5,在进行监测时将损失前5个样本,因此最后由第一个变量子块进行第二层信息提取后扩展成的观测值、累计误差以及二阶差分信息子块分别为X1∈R955×2,X1l∈R955×2,X1d∈R955×2。同理,对剩下所有变量子块进行特征信息提取,8个变量子块扩展为24个特征信息子块。

对每个特征信息子块建立PCA监测模型,得到子块的T2和SPE故障控制限后,本文采用贝叶斯方法将所有子块的结果融合为一个BIC监测指标。对于测试样本xtest,以计算BICT2统计量为例,首先由PCA模型计算出其在每个子块中的故障统计量,然后由式(11)和(12)计算出其在每个子块中出现故障的条件概率(α取0.99),之后根据式(15)得最终的BICT2统计量,同理可得BICSPE统计量。在BIC监测指标下,两种统计量控制限均为1-α即0.01。当样本的监测统计量高于控制限则判断为故障样本。

表2分别给出了针对TE过程的不同故障,3种分块方法,即基于互信息变量分块(Mutual information PCA,MIPCA),多块信息提取(Multi-block information PCA,MBIPCA)以及本文方法HIEPCA下最优子块的监测结果(各故障最低漏报率及对应的故障编号在表2中加粗表示)。

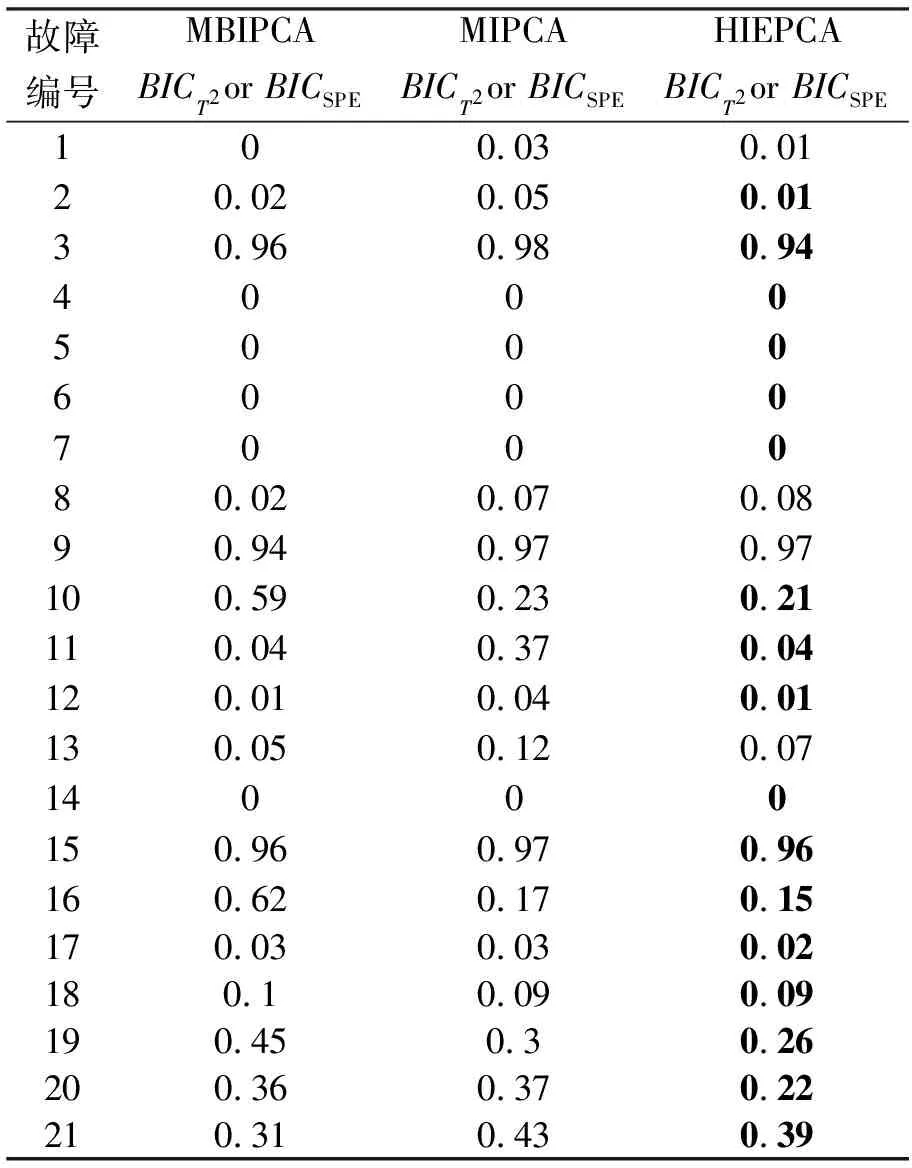
表2 各方法下最优子块漏报率

从表2可以看出,大部分故障情况下本文方法的最优子块的监测结果优于前两种方法的最优子块的监测结果,说明经过局部信息和特征信息提取的两层分块后,子块中包含更多对故障敏感的有效信息,能够获得更好的监测效果。对于故障10和19,最优子块分别为子块14和子块18,即分别对应由变量子块5(含变量18,19,31)所扩展的累计信息误差信息子块和变量子块6(含变量7,13,16,20,27)扩展的二阶差分信息子块,图4和5分别为变量18和27特征信息。

由图4(b)可知,对变量18进行累计误差信息提取后,与原始数据即观测值信息相比,故障样本的数据幅值显著增大,因此更容易检测到此故障。由图5(c)可知,对变量27进行二阶差分信息提取后,正常样本与故障样本差异变得非常明显,更有利于该故障的检测。同时,表3给出了3种方法融合所有子块后最终的监测结果。不难看出,由于进行了分层分块,本文方法在大部分故障情况下的监测结果优于前两种方法。

表3 各方法下TE过程故障漏报率

为进一步说明本文方法的性能,选取故障10和故障20的监测结果做详细分析。故障10为TE过程中进料C温度的随机变化,图6展示了在3种方法下最优子块的监测结果和融合子块后的最终监测结果(图6(a)、(b)、(c)为最优子块监测结果,图6(d)、(e)、(f)为最终监测结果)。在MBIPCA方法中,故障10最优子块的SPE漏报率为65.33%。在MIPCA方法中,最优子块的SPE漏报率为23.28%。在本文方法中,最优子块的漏报率为21.78%,监测效果优于前两种方法的最优子块。融合所有子块监测结果,最终故障10的漏报率仅为15.27%,说明在分层提取信息进行监测能够达到优于单一分块方法的监测效果。

故障20是一种未知故障,其监测结果由图7所示,该故障在MBIPCA方法和MIPCA方法中的最优子块对应的SPE统计量漏报率分别为35.29%和36.8%,监测效果相差不大。在本文方法中,最优子块的SPE统计量漏报率仅为22.53%,为3种方法中最低,融合所有子块的监测结果,最终故障20的漏报率仅为12.39%,大大提升了监测效果。在3种方法的最终监测结果即图(d)、(e)和(f)中也可以看到,MBIPCA和MIPCA方法下的BICSPE统计量与故障控制限有明显相交,而HIEPCA方法中的BICSPE统计量基本都在故障控制限之上,尤其是在第300到第750故障样本点之间,漏报率非常低,监测效果较前两种方法有显著提升。

5 结论

本文提出了一种分层信息提取的多块PCA故障监测方法,在考虑到过程局部信息的同时,挖掘了数据的隐含信息。通过计算过程变量之间的互信息值实现对过程变量分块,基于观测值信息进一步对每个变量块提取累计误差信息和二阶差分信息,实现了局部和特征信息的分层提取,并采用贝叶斯方法对每个子块的监测结果进行融合。TE过程的仿真实验体现了本文方法的有效性和性能,相比于传统的多块监测方法能够获得更好的监测效果。