耐用品垄断市场中的租赁与销售契约

尹训东 许敏波

一、引言

本文首先回顾了消费者类型固定时的耐用品模型中最优的销售契约和租赁契约，然后扩展到消费者类型是随机时的情形。由于可能存在重新谈判，因此本文的分析重点是构建防止重新谈判(renegotiationproof)的契约。防止重新谈判有时间一致性的要求，这种要求排除掉了无效率的后续契约，限制了签订契约双方的合同选择。广义上讲，完全承诺下的最优契约不是防止重新谈判的。

首先，考虑一个销售契约。假设卖家并不知道买家对商品的估值。在静态情形中，卖家可能会把价格设置得足够高以至完全无法卖出，即使他的生产成本已经低于买家的最低估值。然而，一旦买家做出购买的决定会发生什么呢？如果她不买，卖家现在就会知道她的估值很低。此时揭示出来的信息会造成一个以更低价格交易的新机会。事后看这种机会虽然是一种帕累托改进，但是事前看它最终损害了卖家，因为高估值的买家会预期到初始不交易能够让卖家压低价格。重订合同因此也就限制了以事后资源配置的无效率换取垄断高价格的能力。换一种方式讲，这是一个不同于事前全局优化的序贯优化。

事实上，当交易发生时，只要未知信息(uninformed)的一方对已知信息(informed)的一方态度变得更“柔和”(softer)，有效率的重新谈判将会出现。也就是说，只要双方被长期契约保护，他们就不会拒绝达成序贯的、共赢的合同，重新谈判就会出现。

然后，我们考虑一个租赁契约。此时，承诺问题关系到单边合同收益:当双方仅签了短期合同，合同签署后投机行为就会出现，因为随着合同的执行信息能被揭示出来。这是棘轮效应(ratchet effect)的情形(Laffont和Tirole，1988[1])，此时只要未知信息的一方了解到已知信息一方的估值更高，那么未知信息的个体在下一期会要求提供给已知信息个体更加苛刻的合同。然而，未知信息个体的单边收益从事前来看最终会是有害的，因为这可以被已知信息个体预期到。

有两篇论文在耐用品垄断的经济学文献中占有重要地位。第一篇，Coase(1972)[2]讨论了垄断者面临着时间不一致的问题，当他对未来价格做出的承诺不可信时，他不可能行使任何市场力量。第二篇，Bulow(1982)[3]证明了面临时间不一致的企业可以通过租赁代替销售来提高利润。租赁可以减缓时间不一致问题的严重性，而且可能让该企业像非耐用品市场的垄断者那样行使市场力量。然而这一结论依赖于买家匿名的假定:企业面对的是匿名买家的连续集。

我们从一个买者类型在时间上保持不变的例子开始。这里采用的博弈论概念是完美贝叶斯均衡(Perfect Bayesian Equilibrium，PBE)。我们用一个两期的模型，结论表明如果买家是持续匿名的，租赁优于销售。但是如果买家是非匿名的，租赁和销售有同样的结果。

之后，我们分析了允许消费者估值随时间变化的耐用品模型。估值不变的假设在动态模型中是常见的，但是在耐用品的分析中，这是一个很强的假设。估值依赖于世界未来的状态，购买决定也几乎完全是在这些不完全信息的状态下做出的。因此，也就有理由假设耐用品提供的服务流存在一些不确定性。

在本文中，我们考虑消费者存在两种类型的随机估值。其中一种假设买家的保留估值使用Markov转移矩阵更新变化。另一种假设低类型的消费者每一期从一个已知的分布中抽取估值，而高类型的消费者的估值假定是常数，此处高类型假设的简化可以避免复杂的计算细节。

当我们假设消费者的价值(估值)是随时间变化并假设买家的保留估值使用Markov转移矩阵更新变化时，基于买家匿名的假定，科斯假设就不成立了，租赁优于销售的标准结果也就会发生逆转。

从直觉上考虑为什么标准的结果不成立是很简单的。首先，在均衡上高价值的买家总是先于低价值的买家购买。当价值(估值)不变时，一旦一组买家接受了提议，企业就会知道它的剩余需求曲线被截断了，接下来在下一期它将总是会提供一个较低的价格。而当消费者的价值随时间发生变化时，剩余需求曲线中可能会有一些高价值的消费者，他们在前期的价值并没有高到让他们有理由更早购买。这可能会诱使企业在下一期提供一个相对较高的价格来吸取这些新的高类型买家。这些效应往往支撑了一个非单调递减的价格路径。

此外，当价值是随机的时候，销售可能比租赁更有效。比如，假定买家下一期的价值以相等的概率取3或1。如果一个合同在这种不确定性被揭示之前签署，垄断者会完全抽取期望价值(取值为2)。如果一个合同是在买家(而不是卖家)价值实现之后签署的，最优的价格(取值为3)导致期望利润仅有3/2。只要租赁价格是有差别的，在价值实现前签署合同就总能获得潜在的有效收益。

当我们假设低类型的消费者从一个已知的分布中抽取每一期的估值而高类型的消费者估值固定不变。假定随时间变化的估值的买家是非匿名的，我们证明了在一定的事前信念范围内，相对于销售，卖家严格偏好于租赁。取决于卖家关于买家是高类型的事前信念(概率)，卖家将在第一期提供三种合同中的一种，这三种合同分别是:无歧视合同，该合同规定了两期都要消费；一期的有歧视的合同，它提供了一个额外的选项即第一期可以不消费；两期的有歧视合同，它提供了在两期中的一期可以不消费的选项。这正是Hart和Tirole(1988)[4]所分析的情形。而主要的不同点在于两期的有歧视的合同，不像Hart和Tirole文章中两期有歧视的合同，这个合同不会是销售合同，也就是说，它没有规定在第二期以百分之百的概率消费，相反，它包含了一个退出的选项。这样的合同可以用长期的租赁契约来执行。

在不变估值的条件下，没有承诺力的销售合同和长期合同之间是没有差异的。既然估值是不变的，这些合同也就不用解决个人理性在事前和事后之间存在的矛盾。相比较而言，在随时间变化的估值模型中，会有这种矛盾，准确地说是因为低类型的估值在未来可能是高的也可能是低的。在一期的有歧视的合同下，第二期价格是低类型的期望估值。因此，在第二期估值是一个更低值的低类型消费者，他的个人理性约束在二期就不会被满足。所以对于这种二期价格而言，有必要采用长期的契约。更进一步，长期契约允许对买家的估值模式进行更紧密的跟踪。一个两期有歧视的合同可以让买家在他的估值高时消费，低时选择退出。

因此，我们证明了对于一个非匿名的买家，当他的估值是私人信息且随时间变化时，如果长期契约被允许，即使不排除重新谈判，那么租赁契约也可能严格优于销售契约。

Baron和Besanko(1984)[5]分析了私人信息随时间变化的长期合同。承诺和无重新谈判的假设主导着这些分析，这些分析因此也就依赖于显示原理(扩展到多期的设定)。他们分析了在不对称信息(存在逆向选择、道德风险或隐藏信息)下和对称但不可被验证信息下的合同的重新谈判。逆向选择在Hart和Tirole(1988)[4]与Laffont和Tirole(1990)[6]筛选模型中被考虑在内。Maskin和Tirole(1992)[7]考虑了信号模型中的重新谈判。Dewatripont(1989)[8]与Hart和Tirole(1988)[4]考虑了带隐藏信息的合同重新谈判的问题。

本文接下来的内容组织如下。第二节描述了偏好和契约博弈并讨论了当消费者类型固定不变时的科斯动态过程(Coasian Dynamics)。第三节讨论当消费者类型是随时间变化时的最优重新谈判的租赁和销售契约的特征。第四节总结全文。

二、固定类型的模型

我们考虑如下模型:单个商品需要交易，买卖双方都是风险中性，交易在两期进行，买家存在两种类型。具体而言，假设一个买家每期的商品消费估值为vi，满足0＜vL＜vH且Pr(vH)＝β是一个初始的共同知识。而卖家对商品的估值为0。卖家的目标是最大化净期望收益贴现值，而买家的目标是最大化消费估值减去给卖家的支付后的净价值的贴现。双方有共同的贴现因子δ≤1。最后，我们把xit记为类型i的买家在t期消费商品的概率。

定义净价值贴现值如下:Ti是类型i的买家对卖家支付的净价值的贴现值。

(一)完全承诺契约

当卖家自己承诺在未来不会重新谈判时，我们把最优契约的性质表述为如下命题:

证明:在固定类型和完全承诺条件下，显示原理依然有效。两期完全承诺的最优长期契约是最优静态契约的两次重复。最优的静态合同正如命题1所述。证毕。

也就是说，如果低估价的买家的概率足够高，最好是卖给两种类型的买家一个共同的价格vL。如果这个概率足够低，最好是排除掉低类型的买家。

(二)没有承诺力时的销售契约

(1)完全分离的情况:P1＝vH＋δ vL，P2＝vL，卖家收益是π＝β vH＋δ vL；

证明:我们使用逆向归纳求解。在第二期，通过序贯理性，当β(P1)＞β′，P2＝vH；当为其他情况时，P2＝vL。如果P2＝vL，第一期的卖家可以索要的最高价格是P1＝vH＋δvL。这些价格构成了这个博弈中的完美贝叶斯均衡(PBE)，卖家得到的收益为π＝β vH＋δ vL。证毕。

在第二期，卖家也可以在P2＝vH和P2＝vL之间随机化。但是这种情况被半分离的情况占优，因为第一期收益是较低的而第二期的收益等于半分离的情况。

我们可以看到卖家没有承诺力时的收益要低于完全承诺的收益，这是一个非常一般性的结论。

上面的哪种契约是最优的依赖于β的取值，当β→1时，第一期确定卖出要比随机性的选择卖出差一些，因为第一期通过随机化，卖家可以以一个高概率在高价格上卖出。对于β→β′，确定卖出优于随机化的情况，因为随机化意味着在第一期以一个小概率卖出。因此在附近有一个截断值β，当高于它时，随机卖出是一个更好的选择，低于它时确定卖出给H类型是更好的选择。

不做承诺意味着当卖家认为买家的估值很低时，就会降低价格。在第一期确定卖出商品给高估值的买家意味着卖家不得不在第一期收取一个较低的价格，因为买家知道第二期将会是一个低价格。一直保持高价格意味着要接受卖不出去的可能性。当卖家不再期望于第二期从低估值的买家那里得到更高的收益时，一直保持高价格的策略会是有利可图的，因为他遇到这种低估值的买家是一个低概率事件。

(三)没有承诺力时的租赁契约

之前的分析假设的是一个销售契约，现在我们考虑另一种策略——即期租赁契约。也就是说，买家在第一期支付R1且只在第一期消费，卖家在第二期要求一个新的租金R2。

当买家是匿名的，对于垄断者来说租赁优于销售，因为一个租赁方案绕过了承诺的问题:垄断厂商在每期面对的是相同的需求曲线，因为无法追踪有谁已经购买了。

相反地，如果假设卖家面对的是一个非匿名的买家，情况就会发生很大的变化。当卖家认为他正面对一个高类型的买家时，他并不能承诺在第二期不提高租赁价格。高类型的买家同样也会考虑到这种棘轮效应。

(1)完全分离均衡:R1＝(1－δ)vH＋δvL，对于那些在第一期租赁的人，R2＝vH；对于那些不在第一期租赁的人，R2＝vL。卖家的收益是π＝β vH＋δ vL。

证明:解决这一问题的程序和命题2中使用的逆向归纳法是一样的。证毕。

因此，对于两期的情况，我们得到了和销售契约同样的结果。

(四)可以重新谈判的长期契约

我们已经比较了完全承诺的解和不作承诺的解，还有不作承诺即期契约的解。还有另一种长期契约的情况需要考虑:如果卖家可以在第二期期初重新提供一个新的合约来代替原来的合约，并且该新合约对于买家来说更有利。这种帕累托改进的重新谈判合约会带来一个问题，即第二期的帕累托最优可能会损害第一期的帕累托最优。

在可重新谈判的长期契约下，一种可以执行的销售契约的方法如下:

在“完全分离”的情况中，买家在第一期选择接受一个有两个选项的长期合同:她可以在两个时期以vH＋δ vL的价格消费或者仅在第二期以第一期的价格δ vL消费。

在“半分离”的情况中，买家在第一期面临一个总共有三个选项的长期合同:在第一期，她必须选择消费还是不消费商品；如果她选择在第一期消费，那么她在第二期也会接着消费，然后总共支付vH(1＋δ)(在第一期的钱)；如果她不在第一期消费，接下来她在第二期有另一个选择:选择消费并总共支付δ vH或者不消费不支付。

以上例子可以用来说明防止重新谈判原理(renegotiation-proof principle):我们可以用一个防止重新谈判的合同来执行“完全分离”和“半分离”的两种情况。我们可以更广泛地使用这种合同，因为未来预期到的谈判总可以包含在初始的合同中。

虽然对于销售的情况，即期契约和可以重新谈判的长期契约是没有差别的，但是这对于租赁契约的情况并不适用。长期契约确实摆脱了棘轮效应，而之前的长期契约也可以很容易被重新解释为一个防止重新谈判的租赁契约:

在“完全分离”的情况中，买家在第一期选择接受一个有两个选项的合同:她可以以第一期的租赁价格vH和第二期的价格vL在两期都消费，或者她仅仅在第二期以租赁价格vL消费。

在“半分离”的情况中，买家选择接受一个总共有三个选项的合同:在第一期，她不得不选择消费还是不消费商品；如果她选择在第一期消费，那么她在第二期也会接着消费，然后在每一期支付一个租赁价格vH；如果她不在第一期消费，接下来她在第二期有另一个选择:选择消费并支付一个租赁价格vH或者不消费不支付。

因此我们有两个结果:第一，在长期契约和重新谈判下，销售和租赁的结果是一致的，而且也和即期销售契约的结果是一致的。第二，最优的可重新谈判的长期契约可以用防止重新谈判的契约计算。

在超过两个时期的情况下，上面的结果就不正确的了。更一般地，Hart和Tirole(1988)[4]证明了完全承诺的情况下(卖家在初始对整个长期契约有承诺力)，一般会导致对不同类型买家的价格歧视，但是卖家的歧视(discrimination)能力在有限承诺(可重新谈判的长期契约)下会大大削弱，而如果时间范围足够长，这种歧视在没有承诺力(卖家可以仅在每一个时点对一个短期契约做出承诺)的情况下基本会消失。他们还证明了可重新谈判的长期契约的结果等价于没有长期合同的耐用品模型的结果，也就是说，它本质上符合科斯的描述。一种含义是卖家的利润在没有承诺力的租赁模型中是低于销售模型的利润的。

三、估值随时间变化的模型

(一)和马尔科夫式的消费者订合同

我们继续假设消费者存在两种类型。考虑一个市场包含一个企业和一群消费者。首先，我们假设买家是匿名的。每一个买家在每一期有一个估值，它可能高(估值为1)同样也可能低(估值为b)，这里0＜b＜1。卖家不能观察到买家的估值，但是知道在任何给定时间高价值消费者的比例(即需求曲线)。此外，商品是耐用品且以零成本生产。

为了集中考虑个人需求不确定所带来的效应，假设总需求是稳定的。既然转移概率是相等的，这也就意味着在任一给定的时间，所有高类型的消费者所占的比例总是1/2。更进一步，我们只考虑b∈(0，1/2)的情形，这就使得最优情况下不会对所有的买者都出售产品。最后，假定没有二级市场，所有的个体是风险中性且有共同的折旧因子δ。

1.有完全承诺力。

为了和以前的文献保持一致，我们在不同的企业承诺力假设下，计算每种机制下的最优价格。第一种假设是企业可能会以某些方式对未来的价格做出可信承诺。第二种假设企业对价格的承诺是不可能的，此时要求均衡价格是子博弈完美的。我们将这两种假设称为承诺和不作承诺两种不同的情形。我们首先分析了有完全承诺力的租赁和销售策略，然后考虑了不作承诺的情形。

两期的租赁模型:在租赁模型中企业的策略是不同时间上的Rt，每期的租金对应使用商品的那一时期。买家在得知那一期他们的价值后会接受或拒绝企业的租金。

命题4:无论有没有承诺力(消费者是匿名的)，每期的最优租赁价格都是1，企业期望的利润等于(1/2)(1＋δ)。

证明:因为买家不能追踪消费者的估值，租赁价格在选择历史上将会是彼此独立的。所以根据模型的设定卖家在每期以价格Rt＝1租赁是最优的。证毕。

两期销售模型:在销售模型中卖家的策略是价格，这里t时刻的价格仅提供给还没有购买的消费者。买家基于价格历史、当期及将来的期望价值和期望市场价格来接受或拒绝当期价格。当接受该价格并购买，该买家离开市场。如果买家在每一期都拒绝以当期价格购买，那么她不会获得效用。

定义v1和vb分别为高价值和低价值消费者第二期的期望效用，所以有v1≡(1－a)＋ab≥(1－a)b＋a≡vb。首先，我们给出当有承诺力时的最优价格:

命题5:在有承诺时，最优的销售价格是如下两种情况中的一种:

(1)完全分离的均衡价格:P1＝1＋δ v1，P2＝1。高价值的消费者在每一期都会购买，期望的利润是(1/2)(1＋δ(v1＋a))。

(2)混同(pooling)的均衡价格:P1＝b＋δ vb，P2≥vb。所有的消费者在第一期购买，期望的利润等于b＋bvb。

通过比较两个命题中的利润，接下来的推论也就显而易见了。

推论6:在有承诺力的情况下，销售策略总是优于租赁的策略。

当买者价值不变且企业可以承诺时，我们知道销售和租赁是等价的。然而当价值是随机变化的，等价的结论就不再成立。直觉上的解释如下:在第一期，所有高价值的消费者将为第二期使用的商品支付δ v1。如果该企业一直等到这种不确定性被揭示出来(当企业租赁时这种情况将会发生)，比例为1－a的继续保持高价值的消费者将会以δ的现价支付，对于a＞0总利润为δ(1－a)＜δ v1。在消费者的价值实现之前索价是更有利可图的，因为这消除了第二期中信息租金的来源。这被认为是一种效率效应。

2.没有承诺力的销售。

当企业在第二期期初可以改变价格时，上面计算的第二期价格不是最优的。为了研究该问题，现在寻找一个完美贝叶斯均衡(PBE)。首先，我们有如下的结果:

命题7:没有承诺力的情况下，当两种状态转移的概率很高(a≥b)时，销售优于租赁。

证明:当a≥b时，命题5在没有承诺力的情况下依然成立。这是一个PBE。为了更好地看出这一点，首先考虑完全分离的情况，如果仅有高价值的消费者在第一期购买，第二期的最优价格只能是P2＝1因为新的高价值的消费者比例在第二期等于a而该值要大于b。现在考虑混合(pooling)的情况，当所有消费者在第一期购买时，为了构建一个均衡，我们只需让第二期最优的价格大于vb。所以命题5也是一个PBE，因此销售优于租赁。证毕。

命题8:没有承诺力的情况下，给定在两种状态转移的概率比较低(a＜b)，在两期的销售模型中的完美贝叶斯均衡是:

(1)分离均衡:p1＝1＋δb，p2＝b。在第一期高价值的消费者购买，在第二期所有其他的消费者都购买，期望的利润等于1/2＋δb。

(2)半分离均衡:p1＝1＋δ v1，p2＝1。高价值的消费者以概率γ1＝(1－2b)/(1－a－b)接受第一期的价格，在第二期所有的高价值消费者购买，期望的利润等于(1/2)(γ1＋δ(1＋γ1ab))。

(3)混合(pooling)均衡:p1＝b＋δb，p≥vb。所有的消费者在第一期购买，期望的利润等于b＋δb。

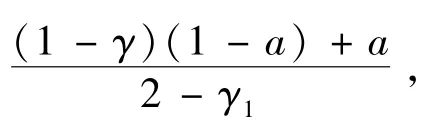
首先，我们考虑完全分离均衡。高类型将会在第一期接受合同，因此在第二期价格将会是p2＝b。所以第一期的最高价格将是p1＝1＋δb。利润是1/2＋δb。

然后，我们考虑第一期的混合(pooling)均衡，因此第一期的价格将会是p1＝b＋δ vb。为了构造均衡，我们必须让p2≥vb。这种情况下的利润是b＋δ vb。

3.没有承诺力时的租赁且买家是非匿名的。

当买家是非匿名的，最优的租赁合同是什么？这又会存在棘轮效应。因为在第一期如果买家在R1＞b时接受合同，这表明他们是高类型的，这样他们在第二期的租金R2＝1。因此高类型的消费者不愿意透漏出他的信息。我们有如下命题:

命题9:在没有承诺力的情况下，假设买家是非匿名的，给定状态间转移的概率是低的(a＜b)，两期租赁模型中的完美贝叶斯均衡是:

(1)R1＝b，R2＝1，卖家的收益是π＝b＋δ/2。

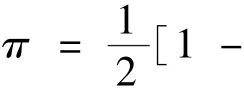
同时，R1＝b和R2＝1也构成均衡。在这种情况下，卖家在第一期混同了两种类型的买者，而在第二期将他们分离开。

卖家选择以上哪种均衡再一次取决于参数的取值。

没有承诺力且消费者为非匿名时，对比卖家在命题7和命题8中销售合同和租赁合同的利润，我们总结为卖家的销售合同也会优于租赁合同。而当消费者的类型是不变时，销售合同和租赁合同是等价的。棘轮效应大大限制了卖家的利润。

推论10:卖家没有承诺能力且消费者是非匿名时，销售策略也总是优于租赁策略。

4.可重新谈判的最优长期合同。

在没有任何承诺力的情况下，销售和租赁合同都是防止重新谈判的。因此，这些合同可以相应地用防止重新谈判的长期合同来执行。但是销售和租赁合同都不是最优的。可以证明，最优机制可以通过租赁合同并且附加一些期权来执行。这些在第一期卖给消费者的期权，会允许消费者第二期以一个事先规定的价格选择购买商品。

(二)独立随机消费者的重新谈判契约

正如在引言中提到过的，我们在这里考虑另一种类型的随机过程(不是马尔科夫过程)。我们考虑这样一种情况:低类型消费者每期的价值是从一个已知的分布中抽取的，而高类型消费者的价值是不变的常数。对高类型这种简化的假设可以避免繁琐的细节。

现在让我们考虑另一种情形，即一个耐用品的垄断者，买家非匿名并且商品所带来的价值随时间变化。该价值是买家的私人信息。

卖家的生产成本为零。买家每期消费0单位或1单位商品。买家有两种类型:高类型H或低类型L。该博弈持续两期。L类型买家每期的价值是从｛vL，vH｝中随机抽取的，其中有0＜vL＜vH。H类型的价值假定不变，就是vH。在每一期低类型L的价值或者以概率q等于vH或者以概率1－q等于vL。假设q＜vL/vH以保证卖家会选择甄别两种类型的消费者。μ1表示卖家认为买家类型是H的事前信念(prior belief)，μ2表示相应的第二期的事后信念(posterior belief)。在任意给定的时期内，一个低类型买家有高(低)价值称为短期的(transient)高(低)类型LH(LL)。买家在博弈期初知道她自己的类型。一个低类型的买家知道她当期的价值，但是不知道下一期的价值。q值和μ1值都是共同知识。回报取决于买家的消费模式和买家支付的价格。买家和卖家假定为风险中性的，他们有共同的贴现因子。买家的回报等于她经过贴现后的期望效用减去期望支付。卖家的回报等于她收到期望支付的贴现值。

1.完全承诺下的情形。

该博弈的时序是:在签订合同前买家知道第一期她自己的价值但是不知道第二期的价值。在卖家有承诺力的情况下，什么是最优的销售和租赁合同？我们知道合同是在第二期类型的不确定性实现之前签订的，因此低类型买者在第二期得不到租金。所以在任何最优的合同中，第二期的价格不会是vL。定义＝qvH＋(1－q)vL。直观上，如果μ1足够大，在第二期卖家将会要价vH，我们将会得到完全分离均衡。因为当卖家要价vH时，我们至少可以获得μ1vH＋(1－μ1)q vH。如果她要价q vH＋(1－q)vL，她最多可以获得qvH＋(1－q)vL。在第一期，卖家必须要价vH或vL。如果μ1足够低，从直觉上这会是一个完全混合(pooling)均衡。当卖家要价vH，期望收益是μ1vH＋(1－μ1)qvH。当卖家要价vL，她可以获得vL。所以在第一期，当且仅当μ1足够低卖家要价vL。在这两种情况之间，我们可能会有部分分离均衡。因此我们有下面的命题。

命题11:在有完全承诺力的情况下，最优的销售契约是:

证明:尽管μ1的表达式有点复杂，但μ1的临界值可以通过比较三种情况的利润被很容易地计算出来。

重点是理解为什么我们的结果一定落入以上这三类。从之前的讨论中，卖家在第二期的要价不会是vL。所以在第二期要价一定是vH或δ[qvH＋(1－q)vL]。因此，在第一期，卖家仅仅有三个选择可以考虑:P1＝vL＋δ[qvH＋(1－q)vL]，P1＝vH＋δ[qvH＋(1－q)vL]和P1＝vH(1＋δ)。μ1的临界值可以通过比较三种情况的利润被很容易地计算出来。证毕。

2.卖家没有承诺力下的销售契约。

再接下来，将会考虑最优的没有承诺力下的销售契约。

命题12:没有承诺力的情况下，两期销售模型中的完美贝叶斯均衡有如下三种:

(1)完全混合(pooling)均衡:在μ1的一些取值范围内，两种类型的买家都在第一期购买，价格是P1＝vL＋δ[qvH＋(1－q)vL]，P2≥vH。

(3)完全分离均衡:在μ1的其他一些取值范围内，P1＝vH＋δ vL，P2＝vL，高类型和短期高类型的消费者在第一期消费。所有其他类型的消费者在第二期购买。

证明:我们继续使用逆向归纳法。因为这是一个销售合同，第二期有两个选择:P2＝vH，P2＝vL。

如果P1＝vL＋δ[qvH＋(1－q)vL]，这就成了混同均衡的情况。所有的消费者在第一期消费，利润是vL＋δ[q vH＋(1－q)vL]。

如果我们让P2＝vL，则P1＝vH＋δ vL。在这种情况下高类型和低类型高价值的在第一期消费。其他类型的消费者在第二期消费。卖家的利润是[μ1＋(1－μ1)q](vH＋δ vL)＋δ(1－μ1)(1－q)vL。

情形(1)中的利润很简单，是P1＝vL＋δ[qvH＋(1－q)vL]。对比每种情况的利润我们可以得到μ1的范围，而该范围决定了(1)、(2)或(3)中哪一种是最优的。μ1的表达式有点复杂，我们没有给出确切的形式，但是可以通过比较每种情况下的利润直接计算出来。证毕。

3.没有承诺力下的租赁契约。

命题13:在没有承诺力的情况下，假设买家是非匿名的，在两期的租赁模型中完美贝叶斯均衡有如下三种:

(2)完全分离均衡:R1＝vH－δ(vH－vL)，对于那些在第一期租赁的，R2＝vH；对于那些不在第一期租赁的，R2＝vL。在第一期仅仅高类型的消费。在第二期，所有类型的都消费。

(3)混合均衡:R1＝vL，R2＝vL，卖家的收益是vL。

证明类似命题12。

4.可重新谈判的长期最优契约。

下面说明当消费者的价值是随时间变化时销售并不是最优的。Hart和Tirole(1988)[4]证明了当价值不随时间变化时(q＝0)，则(1)存在唯一一个防止重新谈判的合同，(2)这个合同是一个销售合同。我们接下来将会看到在价值是私人信息并且随时间变化的模型中，科斯动态是存在的。但是长期最优合同不是一个销售合同。

在我们的模型中，防止重新谈判合同一般不会是销售合同。在两期中差别定价的销售合同所带来的利润并不是最高的，可以带来更高利润的合同可以使所有买家同样好并且该合同是防止重新谈判的。

定义1:合同的长度:合同差别定价的期数被定义为合同长度。

现在，我们引入两个引理。

引理1描述了在什么条件下长度为1的销售合同是防止重新谈判的。引理2说明长度为2的销售合同不可能是防止重新谈判的。我们将使用这两个引理来推导最优的防止重新谈判的合同。

销售合同可以被另一种合同取代，该合同在一期消费后给消费者提供退出选项。在此新合同下，消费一次不代表买家永远消费。这让卖家可以更早甄别出短期高类型和短期低类型的买家。短期高类型的更早消费对于其他类型的激励保持不变。事实上，这种对短期高类型的更早消费使高类型买家在第一期进行消费的概率提高，两者都使得卖家的利润提高。

证明:从时期2开始的长度为1的销售合同意味着分离是最优的。卖家如果从时期2的期初采取分离的策略，那么他将会获得μ2vH＋(1－μ2)qvH。如果他采取混合(pooling)策略，他将会获得vL。所以如果μ2vH＋(1－μ2)q vH≥vL，也就是说，分离是防止重新谈判的。证毕。

证明:基本的想法是在一期消费后我们可以提供一个退出选项，这会使得卖家变好，同时不影响买家的激励相容约束和防止重新谈判的约束。

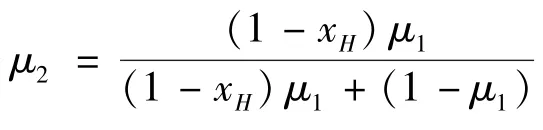
为了使得灵活的合同在第二期防止重新谈判，就只需要检验在第一期消费后H类型的事后概率不超过(引理1)。

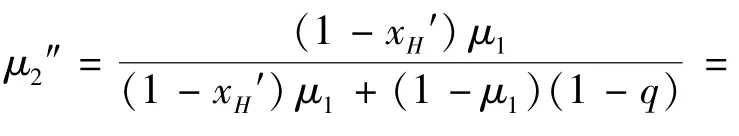
现在，我们在两期模型中刻画最优的防止重新谈判的合同。在均衡时只需考虑三种类型的合同。如果初始的事前信念表明买家是低类型的，卖家将会提供一个无差别的合同。在一个无差别的合同下，所有类型的买者在两期消费的概率都是1。

一期价格歧视(差别)的合同提供了在第一期不消费的选项。在均衡中短期低类型的买者在第一期不消费，他们将只在第二期消费。高类型和短期高类型的在两个时期都消费。在事前信念取一个中间范围时，将会使用该合同。

两期价格差别的合同包括在两期不消费和以1的概率消费的选择。如果卖家遇到高类型的事前概率很高，那么她就会使用这样的合同。在均衡中，短期低类型的且在第二期继续为低价值的买者在两期都会消费。如果她的价值在第二期转变为高的，她将只会在第二期消费。一个短期高类型的在第一期以1的概率消费，只要价值继续为高的，那么她也会在第二期消费。第一期为高类型的在消费和不消费之间随机选择，在最后一期她以1的概率选择消费。

命题14:两期模型中，长期最优的防止重新谈判的合同是:无差别的合同、一期差别合同和两期差别合同。

证明:总的来说，会有六种情况需要考虑。但我们使用引理2可以很容易地比较六种不同的情况的收益并将这些情况减少为以上三种情况的最优合同，也就是无差别的合同，一期差别合同和两期差别合同。可以证明取决于事前信念μ1，每种类型的合同都可能是最优的。

(1)在无差别合同的情况中，所有类型在两个时期都消费。卖家期望利润等于vL＋δ[qvH＋(1－q)vL]。均衡中的最优价格是P1＝vL＋δ[qvH＋(1－q)vL]，P2＞δ[qvH＋(1－q)vL]。

最优契约和相应的事前信念的范围都是随q连续变化的。当q＝0时，这些契约和临界值与Hart和Tirole(1988)[4]得到的结果相同，因为没有了短期高类型，退出的选项也就失去作用。当时，如果事前信念足够大时，最优的合同就与销售合同不一样了。证毕。

情形(1)和情形(2)可以用长期销售契约来执行，情形(3)可以用长期租赁契约来执行。

四、结论

本文考虑了当买家的估值(或价值)是私人信息，并且该价值是随时间固定不变或者随时间发生变化时，卖家和买家之间的最优契约问题。我们在三种假设下分析了这些契约，这三种假设分别是:有完全承诺力(卖家对整个长期契约有承诺力)；跨期没有承诺力(卖家只能在每一期对短期契约有承诺力)；有限承诺力(卖家可以和买家签一个长期契约，但并不承诺不会重新谈判该长期契约)。

当买家的估值不变时，我们证明了在完全承诺力下会导致对不同类型买家实行价格歧视(或有差别的定价)。但是在有限承诺力和完全没有承诺力的情况下，卖家实行价格歧视的能力减小了。在完全承诺力下最优的是分离均衡时，在有限承诺和没有承诺力下最优的合同可能是半分离和混合(pooling)均衡。租赁是否优于销售取决于买家是否匿名的假设。如果买家是匿名的，则租赁优于销售。因为租赁契约解决了时间不一致的问题。然而如果买家是非匿名的，则在两期模型中租赁等价于销售。但是如果超过两期，销售会优于租赁，可重新谈判的长期最优契约等价于销售契约。

当买家的估值是随时间变化时，我们先假设这种变化服从马尔科夫过程。在该情形中，如果有完全承诺力，那么由于效率效应，销售会优于租赁，而当买家的估值不变时，销售和租赁是等价的。在消费者知道他们的价值之前签订合同是更加有利可图的，因为这会消除掉第二期的信息租金。如果没有承诺力并且消费者是匿名的，我们证明了当在两种状态间的转移概率很高时，销售会优于租赁。如果状态间的转移概率是低的，租赁会优于销售。这恰恰是Coase(1972)[2]和Stokey(1981)[10]的观点。如果没有承诺力并且消费者是非匿名的，由于棘轮效应的作用，销售策略总是优于租赁策略。当买家的估值是随机的，销售和租赁都可能不是最优的。我们可以证明，在一般情况下，最优机制可能通过租赁加上一些购买期权来实现。

当我们放弃马尔科夫的假设而假设低类型估值在两个时期是独立的，在没有承诺力的情况下，租赁和销售无法简单地比较优劣。可重新谈判的长期最优契约可以通过将销售和长期租赁结合使用来实现。在估值不变的情况下，没有承诺下的销售和长期契约之间是没有差别的。既然估值保持不变，那么就不存在事前和事后个人理性之间的冲突问题。与此对照的是，因为低类型的估值在未来可能是高的也可能是低的，所以在估值随时间变化的模型中存在这样的冲突。

本文中我们考虑的是两期的情况，将来可以把分析拓展到多于两期的情况。另外，本文的整个分析基于消费者的需求是0或者1的假设，同时我们还假设仅有两个类型的买家。这两个假设的限制性都很强，但即使基于这样的假设的情况，分析也是非常复杂的。在将来的工作中，也可以放松这些假设。

[1]Laffont J J，Tirole J.The Dynamics of Incentive Contracts[J].Econometrica，1988，56(5):1153－1175.

[2]Coase R.Durability and Monopoly[J].Journal of Law and Economics，1972，15(1):143－149.

[3]Bulow J I.Durable-Goods Monopolists[J].Journal of Political Economy，1982，90(2):314－332.

[4]Hart O D，Tirole J.Contract Renegotiation and Coasian Dynamics[J].Review of Economic Studies，1988，55(4):509－540.

[5]Baron D P，Besanko D.Regulation and Information in a Continuing Relationship[J].Information Economics and Policy，1984，1(3):267－302.

[6]Laffont J J，Tirole J.Adverse Selection and Renegotiation in Procurement[J].Review of Economic Studies，1990，57:597－625.

[7]Maskin E，Tirole J.The Principal-Agent Relationship with an Informed Principal，II:Common Values[J].Econometrica，1992，60:1－42.

[8]Dewatripont M.Renegotiation and Information Revelation over Time:The Case of Optimal Labor Contracts[J].Quarterly Journal of Economics，1989，104(3):589－619.

[9]Biehl A R.“Durable-Goods Monopoly with Stochastic Values.”[J]The RAND Journal of Economics，2001，32(3)，pp.565－577.

[10]Stokey N L.Rational Expectations and Durable Goods Pricing[J].The Bell Journal of Economics，1981，12:112－128.