摆线针轮传动中摆线轮齿廓修形技术研究*

赵大兴，明廷伯，余金舫，高 博

(湖北工业大学 机械工程学院，武汉 430068)



摆线针轮传动中摆线轮齿廓修形技术研究*

赵大兴，明廷伯，余金舫，高 博

(湖北工业大学 机械工程学院，武汉 430068)

为确定不同传动要求的摆线针轮传动机构中摆线轮齿廓修形方式及最佳的优化算法，首先对摆线针轮传动中摆线轮齿廓应用最多的“正等距+负移距”和“负等距+正移距”两种组合修形方式进行了分析计算，得到了两种组合修形方式引起的回差大小及修形后摆线轮啮合受力的优劣，确定了不同传动要求的摆线针轮传动机构优先适用的修形方式；对摆线轮齿廓优化算法进行了对比研究，针对“正等距+负移距”组合修形方式确定了优先选用的优化算法；对采用“负等距+正移距”组合修形方式，提出了一种改进的优化算法，将该算法与现有的优化算法进行对比分析，根据实际的装配精度确定了应优先选择的优化算法。

摆线针轮；修形；优化；对比

0 引言

摆线针轮行星传动因具有传动比大，承载能力高，结构紧凑，传动效率高等优点，被广泛应用于各类传动机构中，如摆线液压马达，单级减速双轴型卧式BW型摆线针轮减速器，FA型摆线针轮减速器及机器人用高精度RV(Rotate Vector)减速器都运用到摆线针轮传动。标准的摆线针轮传动，摆线轮与针轮之间属于无侧隙啮合传动，而实际上由于制造误差和装配误差的存在，同时为了装拆方便和保证一定侧隙便于润滑，必须对摆线轮齿廓进行合理的修形[1]。因为不同类型的摆线针轮减速机工作要求不尽相同，如BW型减速器对轮齿受力要求比回差高，而RV减速器对回差要求相对于摆线轮齿受力要高。因此确定不同类型的摆线针轮减速器中摆线轮齿廓的修形方式以及最优的修形量也就显得尤为重要。

目前，对于摆线轮齿廓修形工艺和修形量的优化研究的比较深入。在修形工艺方面，李力行[2]介绍了摆线轮三种最基本的修形方式：移距修形，等距修形和转角修形。对修形后的摆线轮与针轮啮合作用力进行分析与计算。何卫东[3]等人针对摆线轮修形对回差的影响进行了研究，确定了组合修形方式产生的回差。关天民[4]对不同组合修形方式产生的回转角进行了计算分析，对不同组合修形方式适用不同传动要求进行了说明。以上学者虽研究了组合修形后的摆线轮产生的回差及受力特性，但是对不同组合修形方式的优劣没有进行相关的计算来进行对比说明。在修形量的优化方面，关天民[5]对采用“正等距+负移距”组合修形方式获得最佳修形齿廓进行了探讨，推导出了摆线轮最佳修形量的计算公式；焦文瑞[6]通过逼近转角修形齿廓法向变动量曲线，利用MATLAB优化工具箱搜寻出了“正等距+负移距”的最佳修形量；针对采用“负等距+正移距”组合修形方式的修形量确定，关天民[7]给出了满足回转角为0的最佳等距和移距修形量的计算公式。以上学者提出的优化算法由于采用的优化目标不同，优化得到的结果也不尽相同，优化算法之间缺少对比研究。

本文针对上述存在的问题，对分别采用“正等距+负移距”和“负等距+正移距”两种组合修形方式产生的回差和摆线轮受力进行了计算，分析了上述两种组合修形方式的优劣及优先适用的传动要求；对当前不同的优化算法进行了对比研究，确定了不同组合修形方式下相对最优算法。

1 理论基础

1.1 摆线轮修形方式

摆线轮修形方式有以下三种[8]：

(1)等距修形：修磨摆线轮时，将磨轮半径由rrp增加或减少Δrrp，磨出的摆线轮齿廓是标准齿廓的法向等距曲线，规定磨轮半径增加为正，减小为负。

(2)移距修形：修磨摆线轮时，磨轮相对于工作台中心移动一个距离Δrp，使标准的针齿中心圆半径rp发生改变，规定针齿中心圆半径增加为负，减少为正。

(3)转角修形：修磨摆线轮时，磨轮相对于标准位置，沿摆线轮齿厚方向有一个转角Δθ。

由于转角修形不能在齿根和齿顶处产生间隙，所以转角修形一般不单独采用，但是经过转角修形后的摆线轮齿廓与标准的摆线轮齿廓是共轭的，所以经过转角修形后的摆线轮齿廓与标准针轮传动可以保持传动比的稳定及良好的齿面受力。等距与移距的组合修形方式修磨出的摆线轮在主要工作区可以近似与标准齿廓共轭，而在齿根和齿顶处有一定的啮合间隙，所以等距+移距组合修形在摆线轮修形中应用最广，且实际运用最多的是“正等距+负移距”和“负等距+正等距”组合修形方式。

1.2 修形摆线轮齿廓参数方程

由摆线轮齿廓成形及修形方式原理，可以得到包括三种齿廓修形的摆线轮齿廓参数方程如式(1)所示[9]：

(1)

式中：

θ：转臂相对于针轮的转角

rp：针轮分布圆半径

rrp：针轮半径

zp：针轮齿数

zc：摆线轮齿数

A：偏心距

K1=zpA/(rp-Δrp)

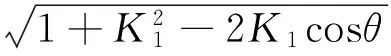
1.3 组合修形引起的回差

经过组合修形后的摆线轮在齿廓的公法线方向与针轮存在着间隙，此时的摆线轮在与标准的针轮传动时会产生回差，回差的大小可按式(2)计算[3]：

Δφ=2(φy+φd)

(2)

其中：

φd=Δrrp/(A·zc)

1.4 修形摆线轮传动受力计算

修形后的摆线轮与针轮传动时，不再属于无侧隙传动，此时只有一对齿最先接触，其余的针轮与摆线轮之间存在一定的间隙Δφi，传递转矩时，摆线轮余针轮齿接触会产生相应的变形δi，只有变形量δi大于该位置初始间隙Δφi的各齿参与啮合。记参与啮合的针齿号为m～n；设最先接触的针齿(受力也最大)所受力为Fb，所受的变形为δmax，传递的转矩为Tc，其余各个位置的摆线针轮副传动力臂为Li，受力为Fbi，其中Fbi与Fb的关系如式(3)所示[11]：

(3)

由力矩平衡可得Fb与δmax两者的关系如式(4)所示：

(4)

忽略影响较小的针齿销弯曲变形，则总的变形量即为接触变形，也即δmax=wmax，而总的变形量与Fb的关系如式(5)所示：

(5)

式中：μ为泊松比，为最先接触点处的摆线轮齿廓曲率半径，c为计算ρ系数；

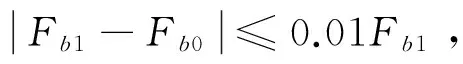
由上述求解过程，在MATLAB中编写了求解最大接触力Fb的的流程图如图1所示。将求得的最大接触力带入到公式(3)中可以得到各个摆线针轮啮合副之间的受力。

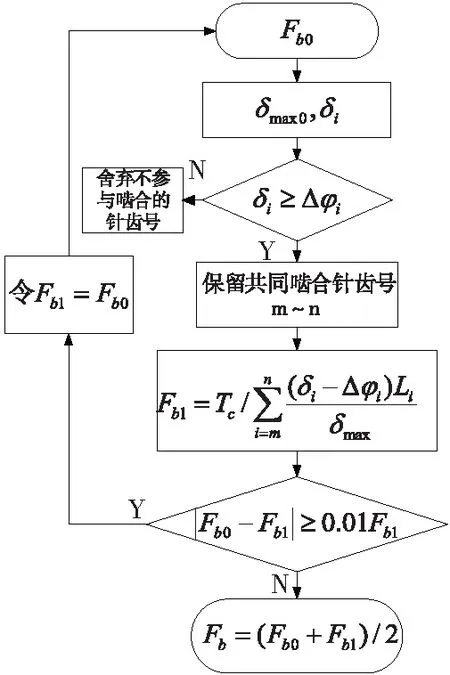
图1 修形摆线轮最大接触力求解图

2 摆线轮修形方式选择

对于一般的摆线针轮传动机构，如摆线液压马达，BW摆线针轮减速器要求齿面受力要好，而对于回差的要求不高；对于高精度减速器如RV减速器，对回差的要求很高[8]，对RV减速器间隙回差根据减速器大小不同不能超过1′～1.5′，加载后包括弹性变形在内的总回差不能超过6′。因此，摆线轮修形方式应根据摆线针轮减速器的传动要求来选择。

以RV320减速器为样机，讨论分别采用“正等距+负移距”和“负等距+正移距”修形方式，摆线轮与针轮的回差及传动受力大小，其中RV320减速器的基本参数见表1。

取齿顶和齿根处径向间隙为Δ=0.03mm，即Δrrp+Δrp=0.03mm，初选文献[7]所提供的确定最佳修形量的方法，可以分别求出当选择“正等距+负移距”和“负等距+正移距”组合修形时的最佳修形量及回差。计算结果见表2。

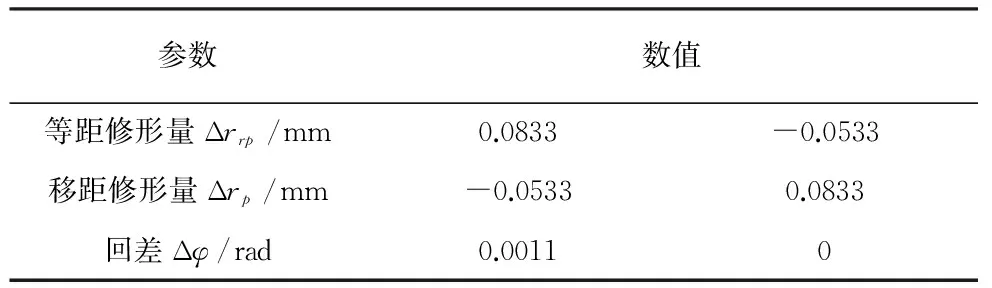
表2 最佳修形量及回差

由表2可知，采用“正等距+负移距”的组合修形方式引起的回差要比“负等距+正移距”大，后者可以满足最小回差为0的条件。将修形量等参数带入到MATLAB编好的包含三种修形方式的摆线轮齿廓参数方程和摆线轮受力的迭代程序中，可以得到修形后摆线轮的齿廓曲线图以及摆线轮与针轮在受载时共同啮合的齿数及各齿所受的力，结果分别如图2和图3所示。

图2 不同组合修形齿廓对比图

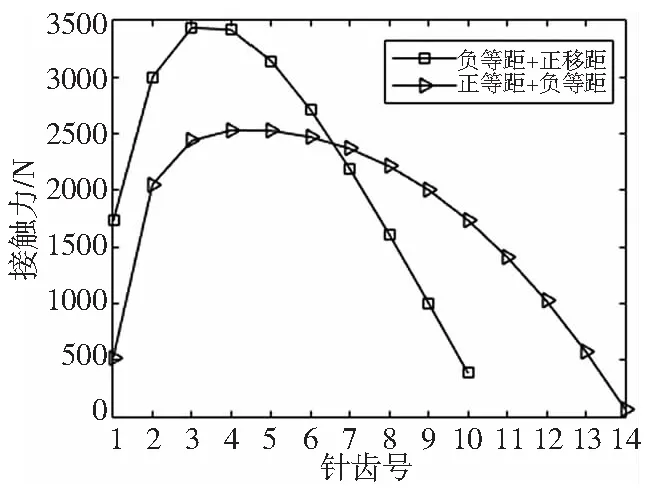
图3 修形摆线轮传动受力图

由图2可知采用“负等距+正移距”组合修形方式的摆线轮齿廓更接近标准齿廓，也印证了其产生的回差较“正等距+负移距”组合修形方式小；而采用“正等距+负移距”组合修形方式的摆线轮齿廓与经转角修形后摆线轮齿廓之间法向距离相对于“负等距+正移距”组合修形方式更均匀，因此，修形后的摆线轮在与针轮啮合时传动应更平稳，受力更好。

由图3可知，当采用“正等距+负移距”组合修形时，在受载时，摆线针轮之间有14个轮齿共同参与啮合，摆线轮齿所受最大的力约为2500N，且轮齿受力变化平滑，各齿受力均衡；而采用“负等距+正移距”组合修形时，在受载时，摆线针轮之间只有10个轮齿参与啮合，摆线轮齿所受的最大力约为3500N，且其余各齿所受力变化较大，各齿受力不均衡。

综上可知，在径向间隙都相同的前提下，经过“正等距+负移距”组合修形方式后的摆线轮在与标准的针轮啮合时，同时啮合的齿数较多，且轮齿受力相对均衡，但引起的回差也较大；而经过“负等距+正移距”组合修形的摆线轮在与标准的针轮啮合时，摆线针轮传动的回差可以控制到很小，但是在与针轮传动时共同啮合的齿数较少，且轮齿受力相对来说较差。因此，对摆线液压马达和一般的BW型摆线针轮减速器应优先选择“正等距+负移距”组合修形方式；对高精度的RV减速器，而应优先选择“负等距+正移距”的组合修形方式。

3 摆线轮齿廓优化

针对采用“正等距+负移距”组合修形方式的摆线轮齿廓的优化，文献[5]和文献[6]选择不同的优化目标得到了对应的最佳修形量，为了叙述方便，将文献[5]中的算法称为算法1，将文献[6]中的优化算法称为算法2；而针对采用“负等距+正移距”组合修形方式的摆线轮，文献[7]给出了满足回差角为0的最佳等距和移距修形量，在本文，提出了另一种基于齿廓法向变动量最小的改进优化算法，同样为了叙述方便，将本文所提出的改进算法称为算法3，文献[7]中的算法称为算法4。

3.1 正等距+负移距修形齿廓优化算法对比

算法1选择的优化目标为：在保证合理的径向间隙的前提下，等距和移距组合修形加工后所产生的摆线轮齿廓和针齿啮合时所产生的的初始间隙最小。依据此优化目标求得的“正等距+负移距”最佳齿廓修形量分别为：

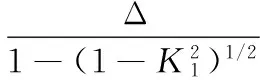
(6)

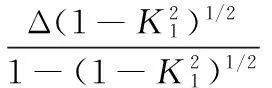
(7)

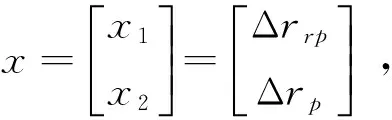
(8)

约束条件为：x1≥0,x2≤0,x1+x2≥0。

考虑到“正等距+负移距”组合修形适用回差要求不高的传动中，且为了计算方便，选定转角修形量Δθ=0.0005rad，n+1=500，在MATLAB中编写算法2的优化算法程序，得到最优的等距和移距修形量，由等距和移距修形量可以得到此时的径向间隙，将此径向间隙带入到算法1的公式中，得到算法1对应的等距和移距修形量。计算结果如表3所示。

表3 算法1和2优化修形量

将得到的最优修形量和给定的转角修形量带入齿廓参数方程中，同样可以在MATLAB中绘制出此时的摆线轮齿廓的曲线图如图4所示，同理可以得到此时各个齿所受的接触力如图5所示。

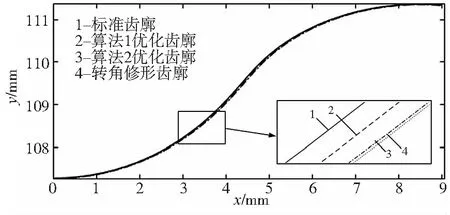
图4 算法1和2优化后的摆线轮齿廓对比图

图5 算法1和2优化后的摆线轮传动受力图

从图4可知，在保证相同的径向间隙的前提下，算法2优化后的齿廓相比于算法1更逼近转角修形后的共轭齿廓；由图5可知，算法2优化后的摆线轮与针轮啮合时，共同啮合的齿数为17对，而经过算法1优化后的摆线轮与针轮啮合传动时共同啮合的齿数为15对；算法1优化后的摆线轮所受的最大力约为2400N，算法2优化后的摆线轮所受最大力约为2000N，且各齿的受力变化较算法1平滑。综上，算法2优化后的摆线轮在传动时受力较算法1好，所以当采用“正等距+负移距”组合修形方式时，应优先选择算法2。

3.2 负等距+正移距修形齿廓优化算法对比

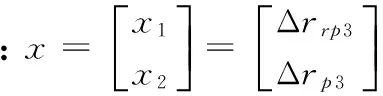
(9)

约束条件为：x1≤0，x2≥0，x1+x2≥0，x1+x2-Δ=0。

算法4给出了满足回差角为0的最佳等距及移距修形量如式(10)和式(11)所示：

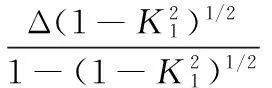
(10)

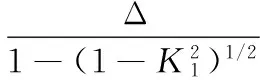
(11)

同样以RV320减速机为例，为了满足小回差要求，选取n+1=500，径向间隙Δ1=0.005mm，Δθ=-0.0001rad，利用MATLAB优化工具箱可以求得算法3和算法4优化的等距及移距修形量如表4所示。

表4 算法3和4优化修形量

由此时的优化修形量可以分别得到二种优化算法的齿廓曲线图如图6所示。

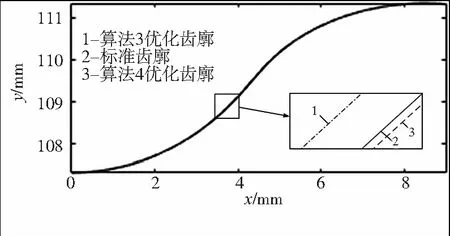
图6 算法3和4优化后的摆线轮齿廓对比图

由图6可知，在保证齿根齿顶处径向间隙相同的情况下，经过算法3优化后的摆线轮齿廓超出标准齿廓且在主要工作段与之存在一定的法线间隙；经过算法4优化后的摆线轮齿廓没有超出标准齿廓，在主要工作段同样与之存在一定的法线间隙。所以在实际装配过程中，当其他零件配合产生的侧隙超过需要的间隙时，算法3优化后的齿廓可以减少这一间隙，减少传动回差；同理，当其他零件配合产生的侧隙较小时，此时摆线轮齿廓优化算法应优先选用算法4。当采用“负等距+正移距”的组合修形时，根据实际装配情况，合理的选择上述两种算法。

4 结论

本文针对摆线针轮传动中摆线轮应用最多的“正等距+负移距”和“负等距+正移距”组合修形方式进行了分析计算，且对两种组合修形方式下的摆线轮齿廓优化算法进行了对比分析，得到了如下的结论：

(1)在相同径向间隙的前提下，“正等距+负移距”组合修形方式较“负等距+正移距”修形方式可以获得更好的轮齿受力，而后者可以获得比前者更小的回差。所以对回差要求不高的一般摆线针轮传动机构应优先选择“正等距+负移距”组合修形方式，对回差要求较高的高精度RV减速器应优先选择“负等距+正移距”组合修形方式。

(2)对于“正等距+负移距”组合修形方式的最佳修形量的确定，用基于逼近转角修形齿廓的优化算法获取的修形量，比用在确定合理间隙的条件下，啮合侧隙最小得到的优化修形量，所得到的轮齿受力更好。当采用“正等距+负等距”组合修形方式时，应优先选择算法2。

(3)对于“负等距+正移距”组合修形，用算法4和本文提供的算法3求解的等距和移距修形量所引起的回差都能够满足回差要求；在实际装配过程中，若由其他零件装配产生的侧隙过大，此时应优先选择算法3。当零件装配产生的侧隙满足要求时，此时应优先选用算法4。

[1] 关天民, 张东生. 摆线针轮行星传动中反弓齿廓研究及其优化设计[J]. 机械工程学报, 2005, 41(1):151-156.

[2] 李力行. 摆线针轮行星传动的齿形修正及受力分析[J]. 大连交通大学学报, 1984, 22(4):32-43.

[3] 何卫东, 李欣. 机器人用高精度RV传动中摆线轮修形对回差影响的研究[J]. 机械传动, 1999(1):24-25.

[4] 关天民. FA型摆线针轮行星传动齿形优化方法与相关理论的研究[D]. 大连:大连交通大学, 2005.

[5] 关天民. 摆线针轮行星传动中摆线轮最佳修形量的确定方法[J]. 中国机械工程, 2002, 13(10):811-814.

[6] 焦文瑞, 孔庆华, 宋德朝,等. 摆线轮齿廓修形的优化设计[J]. 机械传动, 2009, 33(1):41-43.

[7] 关天民. 摆线针轮行星传动中修形所产生的回转误差计算与分析[J]. 组合机床与自动化加工技术, 2001(10):15-18.

[8] 徐灏. 机械设计手册[M]. 北京:机械工业出版社, 2000.

[9] 焦文瑞, 孔庆华, 宋德朝,等. 摆线针轮修形齿廓数学模型的建立与仿真[J]. 机械设计, 2008, 25(11):12-14.

[10] 赵铮. 工业机器人减速器RV320的修形参数优化与工艺性研究[D]. 天津:天津大学, 2013.

[11] 关天民, 张东生, 雷蕾. FA新型摆线针轮行星传动受力分析方法与齿面接触状态有限元分析[J]. 机械设计, 2005, 22(3):31-34.

[12] 赵博. RV减速器摆线轮修形技术与数控成形磨齿机设计[D]. 洛阳:河南科技大学, 2015.

[13] Wang J, Gu J, Yan Y. Study on the Relationship Between the Stiffness of RV Reducer and the Profile Modification Method of Cycloid-pin Wheel[A]. Intelligent Robotics and Applications[C]. Springer International Publishing, 2016.

[14] 张跃明, 耿纪玲, 纪姝婷,等. RV减速器中摆线轮齿形优化修形与参数化设计[J]. 组合机床与自动化加工技术, 2016(3):25-28.

[15] 陈振宇. RV减速器的误差建模与摆线齿廓修形[D]. 天津：天津大学, 2014.

(编辑 李秀敏)

Study on Profile Modification of Cycloidal Gear in Cycloid-pin Gear Transmission

ZHAO Da-xing,MING Ting-bo,YU Jin-fang,GAO Bo

(School of Mechanical Engineering ，Hubei University of Technology，Wuhan 430068，China)

In order to determine the cycloid gear profile modification method and the optimal algorithm of the cycloid-pin gear transmission mechanism of different transmission requirements,the properties of two main combined profile modification methods,“positive isometric + negative shift ”and “negative isometric+ positive shift”,are analyzed and calculated firstly.After the analysis and calculation the backlash and the meshing force of cycloidal gear are obtained.Based on the obtained result,the most suitable modification method of cycloid-pin gear reducer with different transmission requirements is recommended. Then,comparative study on the optimization algorithms of cycloidal profile is operated, and the suitable optimization algorithms of “positive isometric + negative shift ”combined profile modification are determined.Besides,the paper proposes a improved optimization algorithms which applies to “negative isometric + positive shift”combined profile modification and the algorithm are compared with the other algorithm,and the optimal algorithm is determined according to the actual assembly accuracy.

cycloid-pin gear；profile modification；optimization；comparison

1001-2265(2017)06-0045-05

10.13462/j.cnki.mmtamt.2017.06.012

2017-01-06；

2017-02-10

湖北省技术创新专项(2016AAA068)

赵大兴(1962—)，男，武汉人，湖北工业大学教授，博士，研究方向为机械设计、机器视觉检测与质量评价，(E-mail)1982764233@qq.com。

TH132;TG65

A