新型摆线针轮行星减速器的接触变形分析

蒋易强侯 力游云霞张静宇



新型摆线针轮行星减速器的接触变形分析

蒋易强1,2侯 力2游云霞2张静宇2

（1.乐山职业技术学院，四川 乐山，614000；2.四川大学制造科学与工程学院，四川 成都，610065）

摆线针轮行星减速器不仅广泛应用于通用传动领域，而且在机电一体化系统中具有极为广泛的应用潜力。摆线针轮行星减速器的制造精度要求高，轮齿啮合时容易产生干涉、点蚀、胶合以及折断现象，影响减速器的振动、寿命和可靠性。一种带橡胶圈的新型摆线针轮行星减速器被提出，通过有限元方法对比传统、新型减速器的接触变形，新型减速器的关键零件具有更大的变形量。因此，新型减速器能够通过弹性变形实现缓冲和容差作用，进而增强多齿啮合效应，提高承载能力和可靠性。

新型摆线针轮减速器；有限元分析；变形分析

摆线针轮行星减速器具有传动比大、体积小、可靠性高、重量轻、效率高、寿命长等特点。摆线针轮行星减速器不仅广泛应用于通用传动领域，而且在机械人传动、宇航设备、精密机械、超小型传动、测量仪器、微机械和高新技术设备等机电一体化系统中具有极为广泛的应用潜力。但是，摆线针轮行星减速器制造精度要求高，过小的齿轮间隙不利于润滑油膜的形成。在大转矩、瞬时尖峰冲击载荷、强交变载荷、高低温交变等特殊条件下，摆线轮与针齿、柱销套与柱销孔等重要工作表面会发生点蚀、胶合以及折断现象，成为减摆线针轮行星减速器主要的损坏形式，降低齿轮寿命和可靠性。

I·Gu等［1］提出一个利用摆线针轮行星传动达到小回差的构想，并对此构想的轮齿齿廓生成方法进行了研究，对轮齿接触变形和弯曲变形进行了计算分析。S·K·Malhotra等［2］对摆线针轮行星传动进行受力分析，研究不同的结构参数、传动效率对运动构件的接触应力的影响。美国的J·G·Blanche教授［3］对摆线轮使用有限元理论分析了公差配合在摆线轮啮合过程中的影响，建立了有限元模型。Y·K·Taldenko等［4］构建了摆线针轮行星传动的模型，列出齿廓方程和受力方程，研究啮合处的载荷分布、应力分布规律，通过改变设计参数，优化摆线针轮行星传动。Kuen-Bao Sheu、Chen-Fu Chang等［5］对摆线针轮行星传动进行静力学研究，基于D'Alembert理论建立静力学模型，研究效率、阻尼对减速器的影响，为研究几何参数对减速器的静力学影响奠定理论基础。S·Li等［6-8］针对摆线针轮行星传动的轮齿啮合特性和载荷分布情况，运用运动弹性接触理论进行分析，得到最大的载荷分布在轮齿的齿廓接触面上的结论。

邢利娜、陈小安［9］基于针轮对摆线轮啮合作用力的计算公式，采用数学分析软件计算不同修形参数的摆线轮与针轮啮合的相互作用力，得到摆线轮与针轮啮合作用力的变化规律，又对修形和标准摆线针轮行星减速器模型分别进行动力学仿真分析，通过运动曲线验证了模型的正确性，求解出考虑摩擦因素的动态啮合作用力，为工程上进行受力分析、计算提供依据。关天民等［10-11］利用反求设计的研究方法对FA三片摆线针轮行星减速器进行分析，并通过有限元分析方法研究了传动机构的轮齿啮合受力和接触变形，建立了轮齿啮合模型，对摆线针轮轮齿齿廓修形进行了深入的研究。夏显明等［12］建立了摆线针轮行星减速器的三维实体模型，然后把三维实体模型导入到有限元分析软件并进行分析，为进一步优化摆线针轮行星减速器提供方法指导。

以上学者都是针对传统摆线针轮行星减速器进行研究。下面以提高传统摆线针轮行星减速器的寿命、可靠性，减小振动为主要研究目标，利用橡胶材料的弹性变形所具有的缓冲和容差作用，发明一种带橡胶圈的新型摆线针轮行星减速器，并对关键零部件进行接触变形分析。

1 新型摆线针轮行星减速器原理及结构

新型摆线针轮行星减速器主要包括偏心驱动输入机构、减振组件、摆线针轮啮合机构、输出传动机构等四大部分组成，其结构如图1所示。

图1 新型摆线针轮行星减速器结构

偏心驱动输入机构主要由输入轴端盖、偏心套、转臂轴承（I）、转臂轴承（II）、输入轴、输入轴轴承（I）、输入轴轴承（II）组成。减振机构主要由柔性橡胶圈（I）和（II）、转臂轴承套（I）和（II）、转臂轴承套（I）和（II）组成。摆线针轮啮合机构主要由减速器基座、减速器主箱体、针齿销、针齿套、摆线轮（I）和（II）组成。输出传动机构由输出轴、输出轴端盖、柱销、柱销套、输出轴轴承（I）和（II）组成。

新型摆线针轮行星减速器的减振组件是其关键传动件，其详细结构如图2所示。环形橡胶圈18装在转臂轴承套22与摆线轮8之间。为了防止橡胶圈18从转臂轴承套与摆线轮之间滑出，摆线轮中心孔内表面、转臂轴承套外表面、环形橡胶圈的内外表面都具有较大的粗糙度。粘上强力胶的橡胶圈被压装在转臂轴承套与摆线轮之间。

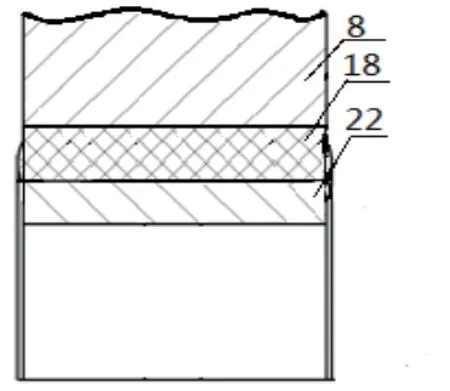
图2 新型减速器减振组件结构

新型摆线针轮行星减速器的特征：在转臂轴承套与摆线轮之间压装减振橡胶圈，试图通过橡胶圈因弹性变形产生的缓冲和容差作用，增强摆线轮多齿弹性啮合效应，提高重载能力的可靠性，过滤由动力源、减速器等因机械能形态改变、啮合冲击、制造误差、装配误差等引起的机械振动波实现，使减速器传递中的高频误差分量得以均化、衰减，并向低频段转移，提高传动精度。特别是新型摆线针轮行星减速器在高低温循环交变或者受到尖峰动态激励等特殊条件下工作时，橡胶圈通过温度、压力引起的橡胶变形使齿轮具有自适应和实时调整的功能。

2 新型摆线针轮行星减速器建模与条件确定

新型摆线针轮行星减速器工况条件，输入轴的转速nH=1440r/min，输入功率P=4kW，传动比i=29，效率η=0.92，每天工作8小时，工作平稳。

材料属性定义是采用有限元法进行静力学分析的前提条件。模型中的针齿销、针齿套、摆线轮、柱销、柱销套的材料均为GCr15，均可将其视为线弹性材料，杨氏弹性模量2.06E+11（Pa），泊松比为0.30，密度为7850（kg/m3）；橡胶圈采用减振橡胶，杨氏弹性模量9.6964E+6（Pa），泊松比为0.47，密度为930（kg/m3）。

摆线针轮行星传动减速器三维模型的网格划分主要采用自由网格划分方法。此方法可以根据模型结构复杂性自行确定网格的疏密，可以减少人为对网格划分的干扰。对于受力复杂、结构简单的零件，如柱销、针齿、转臂轴承套、橡胶圈等进行细化局部网格，提高分析精度。传统摆线针轮行星减速器的网格划分模型包括561372节点数，171257单元数。新型摆线针轮行星减速器的网格划分模型包括562142节点数，171876单元数。

传统、新型摆线针轮行星减速器中各零件之间的运动关系相同，因此施加的边界条件相同。根据摆线针轮减速器的运动原理，对输入轴施加顺时针的旋转副，两个摆线轮及输出轴施加绕各自旋转中心的逆时针的旋转副。根据摆线针轮减速器的受力情况，设置减速器承受自身的重力B、输入轴的顺时针转矩C=26286N-mm、输出轴的逆时针转矩D=707760N-mm、减速器的底面固定约束A。摆线轮与橡胶圈、转臂轴承设为绑定约束；摆线轮与针齿套、柱销套设为无摩擦约束；所有轴承的滚珠与内外圈设为无摩擦接触。摆线针轮行星减速器的受力与约束模型如图3所示；输出轴及柱销旋转副如图4所示。

图3 减速器的受力与约束模型

图4 输出轴及柱销旋转副

3 有限元分析结果及讨论

传统和新型减速器的输入轴的变形量如图5、图6所示。传统减速器的最大变形量为0.0254mm；新型摆线针轮行星减速器的输入轴的最大变形量为0.2561mm；两者差异巨大。

图5 传统减速器的输入轴变形

图6 新型减速器的输入轴变形

传统摆线针轮行星减速器的摆线轮的最大变形量为0.081736mm；新型摆线针轮行星减速器的摆线轮的最大变形量为0.16742mm；两者有较大的差异。

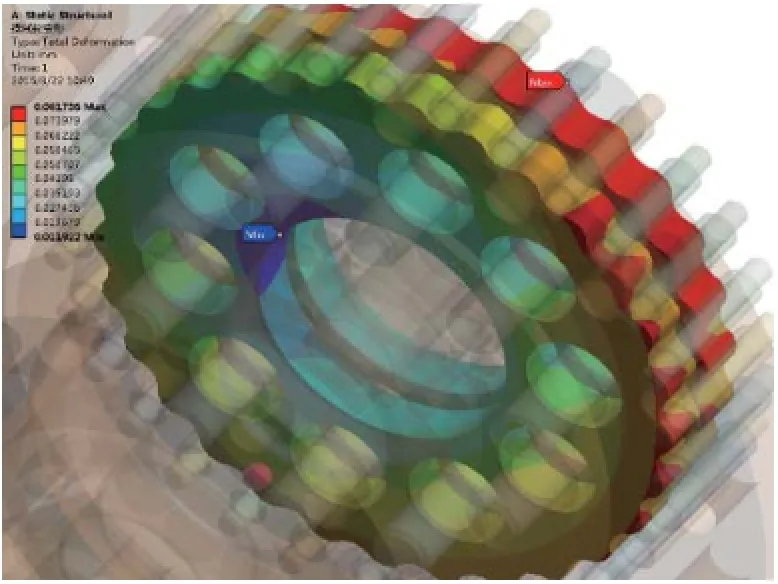
图7 传统减速器的摆线轮变形

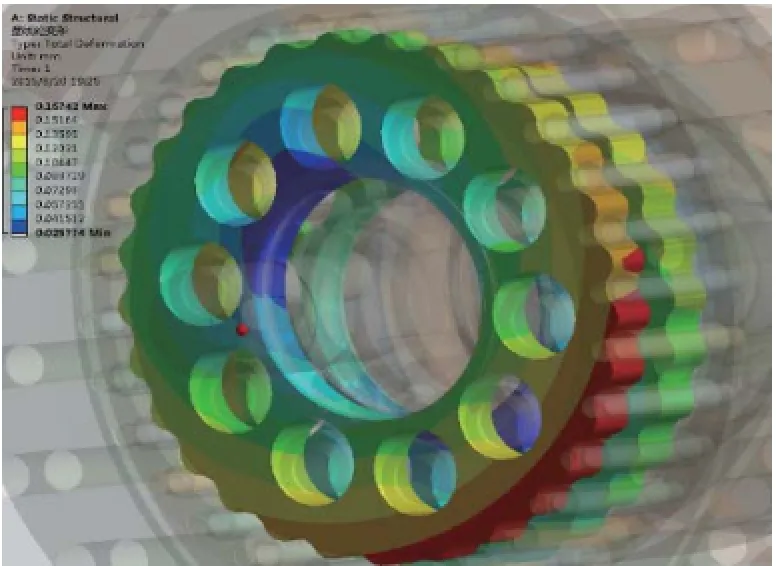
图8 新型减速器的摆线轮变形

传统摆线针轮行星减速器的柱销套的最大变形量为0.076848mm；新型摆线针轮行星减速器的柱销套的最大变形量为0.1214mm；两者有较大的差异。

图9 传统减速器的柱销套变形

图10 新型减速器的柱销套变形

传统摆线针轮行星减速器的输出轴的最大变形量为0.086193mm；新型摆线针轮行星减速器的输出轴的最大变形量为0.1329mm；两者有较大的差异。

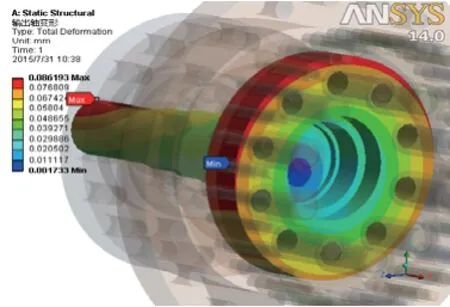
图11 传统减速器的输出轴变形

图12 新型减速器的输出轴变形

转臂轴承套的最大变形0.67544mm，橡胶圈的最大变形0.37313mm。

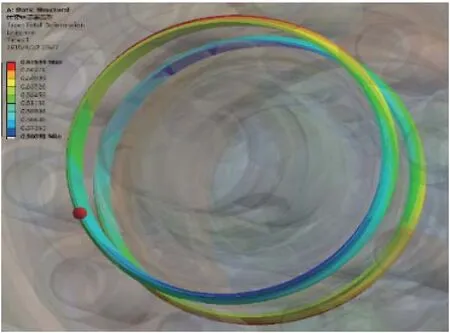
图13 转臂轴承套变形

图14 橡胶圈变形

由此可见，传统摆线针轮行星减速器最大变形量出现在输出轴上，而新型摆线针轮行星减速器最大变形量出现在转臂轴承套和橡胶圈上，变形最大位置发生改变。新型减速器的动力传输零件（输入轴、摆线轮、柱销套、输出轴、转臂轴承套、橡胶圈）变形量比传统减速器的动力输出零件变形量几乎增加一倍。由此可见，新型摆线针轮行星减速器能够通过零件的弹性变形，起到缓冲和容差作用。

4 结论

传统、新型摆线针轮行星减速器的整体以及各零部件的应力对比变化不大，并且满足设计要求。新型减速器的动力传输零件（输入轴、摆线轮、柱销套、输出轴、转臂轴承套、橡胶圈）变形量比传统减速器的动力输出零件变形量几乎增加一倍。由此可见，在大转矩、瞬时尖峰冲击载荷、强交变载荷、高低温交变等外部特殊条件下，以及在齿轮啮合刚度的时变性、齿侧弹性间隙、齿轮啮合误差以及运行过程中零部件的损耗等内部因素影响下，新型摆线针轮行星减速器能够通过零件的弹性变形，起到缓冲和容差作用。

［1］I·Gu. Design of antibacklash pingearing［J］.KSME International Journal，1977，11（6）：611-619.

［2］S·K·Malhotra，M.A.Parameswaran. Analysis of a cycloid speed reducer［J］. Mechanism and Machine Theory，1983，18（6）：491-499.

［3］J·G·Blanche，D·C·H·Yang.Cycloid drives with machining tolerances［J］.Journal of Mechanism，Transmissions，and Automation in Design，1989，111（3）：337-344.

［4］Y·K·Taldenko.Mathematical model of planetary roller-tooth reduction gears［J］. Chemical and Petroleum Engineering，1994，30（3-4）：145-153.

［5］Kuen-Bao Sheu，Chen-Fu Chang. Kinetostatic Analysis of Cycloid Drives［J］. Journal of the Chinese Society of Mechanical Engineers，2003，24（6）：571-581.

［6］S·Li.Contact problem and numeric method of a planetary drive with small teeth number difference［J］.Mechanism and Machine Theory，2008，43：1065-1086.

［7］S·Li.Gear contact model and loaded tooth contact analysis of a threedimensional，thin-rimmed gear［J］.Journal of Mechanical Design，2002，124（3）：511-517.

［8］S·Li.Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors，assembly errors and tooth modifications［J］.Mechanism and Machine Theory，2007，42（1）：88-114.

［9］邢利娜，陈小安.摆线针轮传动啮合力分析及动力学仿真［J］.现代制造工程，2011 （3）：130-133，73.

［10］关天民，雷蕾，孙英时等.FA新型摆线针轮行星传动装置的反求设计［J］.中国机械工程，2003，13（1）：68-71.

［11］关天民，张东生，雷蕾.FA新型摆线针轮行星传动受力分析方法与齿面接触状态有限元分析［J］.机械设计，2005，22（3）：31-34.

［12］夏显明，余建国，刘志强.减速器摆线轮的有限元分析研究［J］.制造业信息化，2005，28（3）：65-66.

A Deformation Analysis of New-type Cycloid Speed Reducer

JIANG Yi-qiang1，2，HOU Li2，YOU yun-xia2，ZHANG jing-yu2
（1. Leshan Vocational & Technical College， Leshan，Sichuan 614000；2. School of Manufacturing Science and Engineering， Sichuan University， Chengdu， Sichuan 610065）

Cycloid speed reducers have been widely used in various fields of common transmission. Besides， cycloid drives have also had great potentials for the application in the fields of mechatronics system. The precision of manufacturing cycloid speed reducers is highly required and therefore when the gear teeth are engaged， phenomena such as interference， pitting， agglutination and fracture are subject to change more likely to appear， which affects the vibrations of the reducer， as well as its life span and reliability. This paper proposes a new type of cycloid speed reducers and compares the contact deformation of both the traditional and new-type speed reducers by adopting the finite element method. The critical parts of the new-type reducer have higher deflections. Therefore， the new cycloid speed reducers are able to function better in the buffer and tolerance by elastic deformation， strengthen the multi-teeth meshing effects and improve its bearing capacity and reliability.

a new type of cycloid speed reducers； finite element method； analysis of deformation

蒋易强（1976—），男，四川安岳人，博士，副教授，研究方向为计算机仿真研究。

TH132.4

A

1674-3083（2016）03-0001-05

2016-02-27