MEA优化BP神经网络的电主轴热误差分析研究*

谢 杰，黄筱调,，方成刚,，张 虎，周宝仓

(1. 南京工业大学 a.机械与动力工程学院；b.江苏省工业装备数字制造及控制技术重点实验室，南京 210009；2. 重庆大学 机械传动国家重点实验室，重庆 400044)



MEA优化BP神经网络的电主轴热误差分析研究*

谢 杰1a，黄筱调1a,1b，方成刚1a,1b，张 虎1b，周宝仓2

(1. 南京工业大学 a.机械与动力工程学院；b.江苏省工业装备数字制造及控制技术重点实验室，南京 210009；2. 重庆大学 机械传动国家重点实验室，重庆 400044)

针对磨齿机在磨削加工时，电主轴存在热致误差等问题，提出一种基于思维进化算法(MEA)优化BP神经网络建立磨齿机电主轴热误差预测模型的方法。通过测量磨齿机电主轴在加工过程中的温升与位移情况，利用思维进化算法优化BP神经网络算法在MATLAB软件中建立预测模型，并与未经过算法优化的BP神经网络建立的模型进行了对比。在电主轴X向热误差预测实验中，未经过算法优化的BP模型最低补偿率为84.85%，而经过思维进化算法优化BP模型最低补偿率为95.29%。结果表明：经过思维进化算法优化BP神经网络建立的热误差模型，在拟合和预测精度上要优于未经过算法优化的BP神经网络热误差模型。

热误差；电主轴；思维进化算法；BP神经网络

0 引言

热误差是精密机床最主要的误差源之一。经研究表明，由机床热变形引起的热误差占机床总误差的40%～70%[1]。而电主轴是机床的关键部件，其热误差直接影响机床的加工精度。为了减少电主轴热误差对机床加工精度的影响，国内外专家学者已经提出了很多改善的方法。大致分为以下三类：热误差避免法、热误差控制法和热误差补偿法。热误差避免法和热误差控制法都需要改进电主轴的材料或结构，这使得制造电主轴的成本上升。而热误差补偿方法是通过分析测试、建立热误差补偿模型，并将其输入到数控系统，实际加工时机床根据已建立的热误差补偿模型预测热误差，进行实时补偿[2]。这种方法无需更改主轴的结构，而且比较经济，被国内外学者广泛研究。因此，如何高效的建立电主轴热误差和温度之间的模型，将直接影响机床的加工精度。

近年来，国内外学者研究了很多建立热误差模型的方法。李旸等[2]利用有限元分析法对主轴温度场和热变形进行了预测，根据测试结果建立了主轴热误差模型，并对热误差进行补偿，有效地保证加工精度。代贵松等[3]利用ANSYS软件对电主轴进行热特性进行仿真分析，得到电主轴的稳态温度场与稳态变形场。由于精密数控机床的热误差受到众多复杂变量相互耦合的影响，故在理论模型计算过程中很难获得机床或机床部件中关键的热态分析边界条件[4]。为了克服理论模型计算过程中的不足，建立较高精度的热误差模型，人们研究了许多人工智能算法来建立热误差模型。雷春丽等[5]提出采用多元自回归方法建立电主轴热误差模型，并通过试验验证该模型的有效性，但是多元回归模型的设计比较耗时和繁琐。Jun Yang等[6]提出基于最小二乘向量机建立热误差模型，结果表明使用这种方法预测的热误差模型精度很高。尽管这种方法在一定程度上可以很好的预测热误差，但热变形通常随着加工过程和环境的变化而变化，将会有其他的误差引入，降低了模型的预测精度。姜辉等[7]提出一种基于贝叶斯推断的最小二乘支持向量机建模方法，结果表明，该模型在机床变工况条件下仍具有较高鲁棒性与泛化能力，可以很好地弥补现有建模方法的局限性。AliM Abdulshahe等[8]提出自适应神经模糊推理系统(ANFIS)建模技术，它将人工神经网络的学习规律与模糊逻辑理论良好的结合。Yang Li等[9]基于多变量输入，分别利用多元回归方法和反向传播网络建模，比较了两种模型的建模精度。苏宇锋等[10]采用BP神经网络建立电主轴热误差补偿模型，结果表明BP神经网络模型能够补偿大部分热变形。但是单一的反向传播(BP)神经网络模型可以很容易陷入局部极小，其多峰值的收敛性是非常差的，所以它是难以获得全局最优解。Yanqun Huang等[11]采用遗传算法优化的BP神经网络的初始权重和阈值，对高速主轴进行热误差建模，结果表明其预测的模型精度大大提高，但是遗传算法存在早熟和收敛速度慢等问题。

为了避免遗传算法优化的BP神经网络中存在的早熟和收敛速度慢等问题，本文提出了一种新的优化BP神经网络的算法，即采用思维进化算法(MEA)优化BP神经网络建立电主轴热误差模型。思维进化算法中的趋同和异化操作可避免遗传算法中的交叉与变异算子出现双重性的问题，提高了模型的稳定性和鲁棒性。因此，采用思维进化算法优化BP神经网络的初始权值和阈值，不仅可以有效的解决全局最小搜索问题，而且可以解决进化算法中的早熟和收敛速度慢的问题[12]。

1 MEA优化BP神经网络模型描述

使用思维进化算法优化BP神经网络过程包括三个方面：确定BP神经网络的结构，思维进化算法的优化和神经网络预测。思维进化算法优化BP神经网络的基本思想是首先通过思维进化算法迭代，寻找并输出最优个体，按照编码规则进行解码，产生BP神经网络的初始权值和阈值。然后将优化得到的初始权值和阈值赋值给网络，再进行网络的训练，最后可实现仿真预测。

思维进化算法优化BP神经网络的流程图如图1所示。

图1 设计步骤流程图

1.1 BP神经网络构建

采用BP神经网络预测热误差模型，其中输入和输出单元数目取决于具体的实验要求。实验中，在高速电主轴四个不同的温度敏感点处设置四个温度传感器并测量三个方向的热误差(X，Y和Z)作为输出，但实际上，由于砂轮与工件沿机床坐标系Z方向的热误差仅影响齿面在齿轮圆周上的位置，而对齿面本身不会产生任何误差[13]，故忽略电主轴Z向的热误差，仅测量X和Y两个方向的热误差作为主要有效值；因此，输出简化为X和Y两向的热误差。从而，建立一个三级BP网络神经结构(图2)，其中输入层的单元数设为“4”，隐藏层单元数为“20”和输出层单元数为“2”。分别采用正切S型传递函数tansig和线性传递函数purelin作为隐藏层和输出层的函数。使用trainlm函数来训练网络，迭代次数设置为50，学习速度为0.1，误差平方和为0.001(表1)。

图2 电主轴BP神经网络热误差模型

表1 BP神经网络参数

1.2 思维进化算法的参数设定

利用思维进化算法对BP神经网络的初始权值和阈值进行优化。首先，根据BP神经网络的拓扑结构，将解空间映射到编码空间，每个编码对应问题的一个解。这里选择BP神经网络的拓扑结构为4-20-2，即输入层有4个节点，隐含层有20个节点，输出层有2个节点，共有4×20+20×2=120个权值，20+2=22个阈值，所以思维进化算法个体编码长度为142。然后，选取训练集的均方误差的倒数作为各个个体与种群的得分函数，利用思维进化算法，经过不断的迭代，输出最优个体，并以此作为初始权值和阈值，训练BP神经网络。思维进化算法的参数如表2。

表2 思维进化算法参数

2 电主轴热误差模型的建立

2.1 电主轴热误差实验

对某公司的大型磨齿机SKMC-3000/20上的电主轴进行热误差测量实验。这个电主轴系统由内置电机和主轴构成，它是独立于整个数控机床结构外的一个零件。其中包括内置电机、主轴、轴承、冷却系统和伺服控制系统等。由于内置电机直接驱动主轴旋转，这就会导致电机与轴承以及主轴与轴承之间产生摩擦热。

采用热电阻(Pt100)传感器和LTS-25-02型激光位移传感器分别记录测量点的温升、位移情况。传感器布置如图3所示。其中，热电阻传感器的测量精度为0.01℃，激光位移传感器的测量精度为0.01μm，电主轴工作转速为1800r/min。

为了尽可能多的获得磨齿机电主轴的温度变化和热误差数据，提高模型的预测精度，每分钟采集一次电主轴温度和位移数据，总共采集了300组数据，耗时300min，得到了如图4所示的电主轴随时间T的温升变化曲线，图5的电主轴随时间T的热误差变化曲线。

图3 电主轴热误差测量实验

图4 电主轴温升图

图5 电主轴热误差变化曲线图

图4电主轴温度变化曲线图中，电主轴转轴头部的温度略低于电主轴根部的温度，这是由于电主轴转轴头部靠近冷却系统，当电主轴工作时，冷却液带走一部分热量，故靠近电主轴转轴头部的温度低于电主轴根部的位置。电主轴在工作240min后，其表面温度达到热平衡状态。

图5电主轴的热误差变化曲线中，可以发现电主轴热误差随着温度的升高而增加，电主轴在工作270min后，其热变形达到最大，且滞后于温度上升一段时间。X向的最大热误差为31.3962μm，而Y向的最大热误差为21.9986μm。由此可见，电主轴热致误差值并不是很大，这就对热误差预测模型的预测精度和鲁棒性有很高的要求。

2.2 热误差模型的建立和模型预测的结果

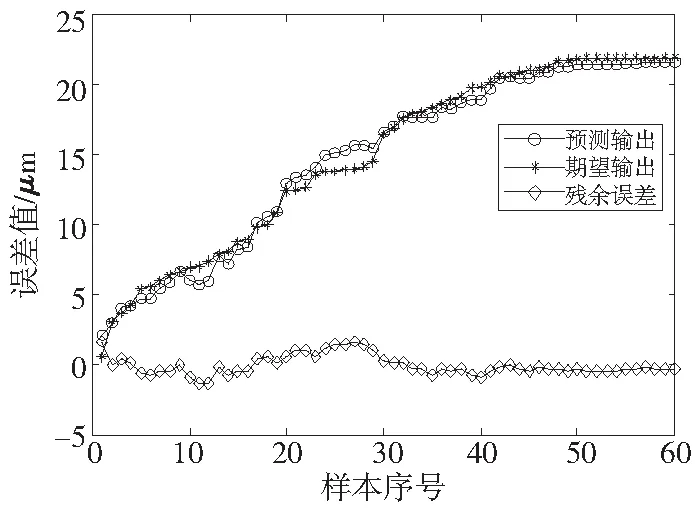
将电主轴热误差实验中所测量的300组温度与热误差数据导入到MATLAB软件中，其中随机选取240组数据作为原始数据，以此训练思维进化算法与BP神经网络模型，建立电主轴热误差模型。利用剩余60组数据进行模型验证。图6为用思维进化算法优化BP神经网络预测模型的热误差拟合图像。图7为用未经过算法优化的BP神经网络预测模型的热误差拟合图像。

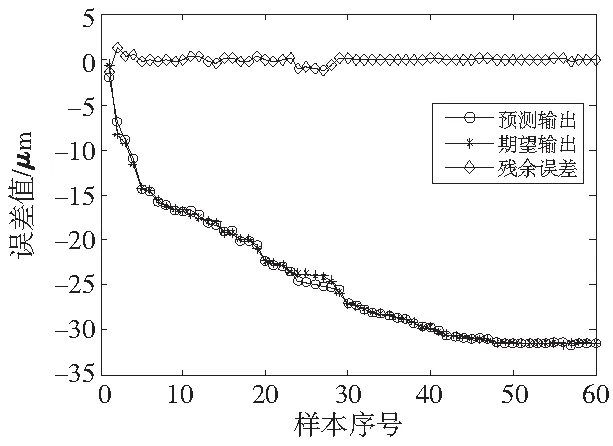
(a)X向预测模型

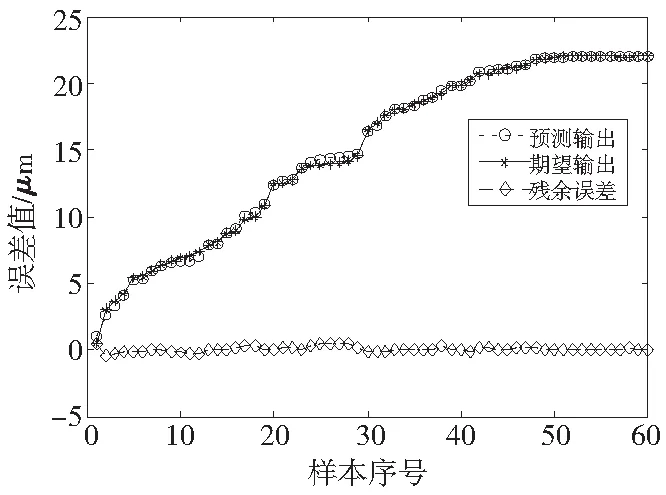
(b) Y向预测模型图6 经MEA优化的BP神经网络预测模型

经MATLAB软件拟合，可以得到经思维进化算法优化的BP神经网络建立X向热误差模型的均方差为Eopti-x=0.1648，而未经过算法优化的BP神经网络建立的X向热误差模型的均方差为Eorigi-x=1.5690。

经思维进化算法优化BP神经网络建立Y向热误差模型的均方差为Eopti-y=0.0396，而未经过算法优化的BP神经网络建立Y向热误差模型的均方差为Eorigi-y=0.5048。

综上所述，经过思维进化算法优化BP神经网络所建立的热误差预测模型的均方差比未经过算法优化的BP神经网络小(Eopti-x

(a)X向预测模型

(b) Y向预测模型图7 未经算法优化的BP神经网络预测模型

3 结果

试验结果如表3所示，列出了磨齿机电主轴热误差预测模型的主要精度指标。

由表3可知，思维进化算法优化BP神经网络建立的X向热误差模型的最大残差为1.4787μm，最低补偿率为95.29%；而未经过算法优化的BP神经网络建立的X向热误差模型的最大残差为4.7580μm，最低补偿率为84.85%。思维进化算法优化BP神经网络建立的Y向热误差模型的最大残差为0.5055μm，最低补偿率为97.70%；而未经过算法优化的BP神经网络建立的Y向热误差模型的最大残差为2.2543μm，最低补偿率为89.75%。

表3 预测模型的主要精度指标

结果表明，通过思维进化算法优化BP神经网络建立热误差模型的预测精度是高于未经过算法优化的BP神经网络所建立的热误差模型。基于思维进化算法优化后的BP神经网络的稳定性和泛化能力大大提高。因此，模型预测更精确。故采用思维进化算法优化BP神经网络建立热误差模型可以更准确的预测电主轴的热误差，提高磨齿机的加工精度。

4 总结

为了减小电主轴的热误差在磨齿机加工过程中对齿轮加工精度的影响，以某公司制造的大型数控成形磨齿机SKMC-3000/20上的电主轴为研究对象，采用思维进化算法优化BP神经网络的初始权值和阈值，在MATLAB软件中训练BP神经网络，建立电主轴热误差预测模型，并与未经过算法优化的BP神经网络建立的模型相比较，结果表明，采用思维进化算法(MEA)优化BP神经网络建立的模型在预测精度上有了较高的改善，泛化能力和鲁棒性明显提高。

[1] Bryan J. International status of thermal error research[J].CIRP Annals-Manufacturing Technology , 1990,39(2):645-656.

[2] Li Yang , Zhao Wanhua .Axial Thermal Error Compensation Method for the Spindle of a Precision Horizontal Machining Center[C]. 2012 IEEE International Conference on Mechatronics & Automation, Chengdu, 2012:2319-2323.

[3] 代贵松,袁峰,张余升,等.电主轴热特性分析与基于自然指数的热误差建模[J].机床与液压,2014,42(17):9-13.

[4] 王海同,李铁民,王立平,等.机床热误差建模研究综述[J].机械工程学报,2015,51(9):119-128.

[5] 雷春丽,芮执元.基于多元自回归模型的电主轴热误差建模与预测[J].机械科学与技术,2012,31(9):1526-1529.

[6] Jun Yang , Shi Hu , Feng Bin,et al. Thermal error modeling and compensation for a high-speed motorized spindle[J]. International Journal of Advanced Manufacturing Technology, 2015,77(5-8): 1005-1017.

[7] 姜辉,杨建国,姚晓栋,等.数控机床主轴热漂移误差基于贝叶斯推断的最小二乘支持向量机建模[J].机械工程学报,2013,49(15):115-121.

[8] AliM Abdulshahed, Andrew P Longstaff, Simon Fletcher. The application of ANFIS prediction models for thermal error compensation on CNC machine tools[J].Applied Soft Computing, 2015, 27(C) : 158-168.

[9] Li Yang, Zhao Wanhu, Wu Wenwu,et al. Thermal error modeling of the spindle based on multiple variables for the precision machine tool[J]. International Journal of Advanced Manufacturing Technology,2014, 72 (9-12):1415-1427.

[10] 苏宇锋,袁文信,刘德平,等.基于BP神经网络的电主轴热误差补偿模型[J].组合机床与自动化加工技术,2013(1):36-38.

[11] Huang Yanqun, Zhang Jie, Li Xu, et al. Thermal error modeling by integrating GA and BP algorithms for the high-speed spindle[J]. International Journal of Advanced Manufacturing Technology, 2014,71( 9-12): 1669-1675.

[12] 王小川,史峰,郁磊,等.MATLAB神经网络43个案例分析[M].北京：北京航空航天大学出版社，2013.

[13] 张虎.数控成形磨削齿面误差理论与修正方法研究[D]. 南京: 南京工业大学, 2014.

(编辑 李秀敏)

Thermal Error Analysis Based on MEA Optimized BP Neural Network for Motorized Spindle

XIE Jie1a, HUANG Xiao-diao1a,1b, FANG Cheng-gang1a,1b, ZHANG Hu1b, ZHOU Bao-cang2

(1 a.School of Mechanical and Power Engineering; b. Jiangsu Key Laboratory of Digital Manufacturing for Industrial Equipment and Control Technology, Nanjing Tech University, Nanjing 21009, China; 2.State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China)

To improve the problem of heat induced error of motorized spindle in grinding machine, a method based on mind evolution algorithm (MEA) to optimize BP neural network to establish the thermal error compensation model of grinding machine motorized spindle was proposed. By measuring temperature and displacement of the grinding machine motorized spindle in the process of machining, the MEA was used to optimize the BP neural network algorithm to build a predictive model in MATLAB software, and the model was compared with the BP neural network which has not been optimized. In theXdirection of motorized spindle thermal error prediction experiment, the minimum compensation rate of the BP model without the algorithm optimization was 84.85%, and the minimum compensation rate of the optimized BP model was 95.29%. The results show that the thermal error model of BP neural network which optimized by the mind evolution algorithm is superior to the BP neural network thermal error model without algorithm optimization in the fitting and forecasting accuracy.

thermal error; motorized spindle; mind evolutionary algorithm ; BP network model

1001-2265(2017)06-0001-04

10.13462/j.cnki.mmtamt.2017.06.001

2016-09-07

国家自然科学基金项目(51635003)

谢杰(1992—)，男，江苏泰州人，南京工业大学硕士研究生，研究方向为数控技术，(E-mail)tzxiejie1992@163.com。

TH161;TG659

A