柔性铰链可倾瓦轴承不平衡响应的主动控制*

常 江，马金奎，路长厚，陈淑江

(山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061)



柔性铰链可倾瓦轴承不平衡响应的主动控制*

常 江，马金奎，路长厚，陈淑江

(山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，济南 250061)

在轴承转子系统中，为提高转子的旋转精度，对系统进行了主动控制。基于柔性铰链可倾瓦轴承建立了轴承转子系统轴心轨迹和轴瓦摆动的计算模型，在考虑系统惯性和非线性油膜力的基础上，计算了转子在不平衡响应下的非线性轴心轨迹和轴瓦的摆动规律，并提出了一种振动的主动控制方法。仿真计算结果表明，转子的不平衡载荷是转子产生周期性振动的重要因素。通过在轴瓦的瓦背施加力，控制轴瓦的摆动规律，可以抵消转子不平衡载荷引起的振动。通过主动控制，转子振动明显减弱，极大得提高了转子的旋转精度。

柔性铰链可倾瓦轴承；不平衡响应；轴瓦摆动；轴心轨迹

0 前言

滑动轴承具有多种结构形式，可倾瓦轴承是滑动轴承的一种，由于其轴瓦可以绕支点进行摆动，因此具有优良的动力特性以及稳定性，被广泛应用于高速旋转机械，但也同时存在着结构复杂、制造成本高等不足之处[1]。国内外众多学者对可倾瓦轴承的结构形式做了许多改进。刘思涌等[2]通过在轴瓦支点与轴承体之间设置弹性垫片，增加了支点的弹性和阻尼，对油膜涡动具有很好的抑制作用。黑棣等[3]设计了固定瓦-可倾瓦轴承，将不稳定的非承载瓦改变为固定瓦结构，运转时转子振动比同参数下普通可倾瓦轴承振动要小。

柔性铰链是对普通可倾瓦轴承结构上的一种创新型设计，将轴瓦的支点改成柔性铰链支承，既简化了轴承结构，又继承了普通可倾瓦轴承的优良性能[4-5]。Kyuho[6]等运用高斯迭代计算了不同转速下转子的轴心轨迹，通过改变轴承参数降低了转子在运行时的振幅，但没有从主动控制角度进行讨论。Pengju Li[7]等讨论了柔性铰链可倾瓦轴承在高速重载工况下系统温度的变化情况。David A.W等[8]通过轴承试验台测出了柔性铰链可倾瓦轴承转子系统失稳转速的大小。

随着现代工业科技的高速发展，对旋转机械也提出了更高的要求。旋转机械在朝着高精度、高转速、高负荷目标发展的过程中，非线性因素对旋转机械振动的影响也越来越突出，转子由于制造误差产生了不平衡载荷会使系统运转中产生强烈的振动。Pixiang Lan[9]等计算了不同工况条件下可倾瓦轴承的非线性轴心轨迹，比较了不同几何参数对系统稳定性的影响。文献[10]计算了普通圆柱轴承转子系统在不平衡载荷作用下非线性轴心轨迹的周期特性，并通过在轴上施加力控制预定轨迹。文献[11]研究了可倾瓦轴承的主动控制模型，通过在轴瓦上开静压腔，采用PI及PID主动润滑控制系统，成功降低了转子振动。Lihua Y等[12]在可倾瓦轴承支点弹性的基础上通过主动控制支点径向位置实现了转子振动的减弱。

本文基于柔性铰链可倾瓦轴承建立了轴承转子系统轴心轨迹及轴瓦摆动的计算模型，运用欧拉方法[13]和四阶五级Runge-Kutta-Felhberg算法[14]得出了转子在不平衡载荷作用下的轴心轨迹及轴瓦摆动规律。提出了一种新的主动控制的方法，即通过在轴瓦瓦背施加力抵消不平衡载荷的影响，达到主动控制转子振动、提高转子旋转精度的目的。

1 轴承模型

四瓦柔性铰链可倾瓦轴承模型如图1所示，图中Ob为轴承中心，Oj为转子中心，θ为角坐标，δi为第i块轴瓦的摆角，规定逆时针方向摆角为正，相反为负。σ为轴瓦张角。βi为第i块轴瓦支点的位置角。ω0为转子旋转的角速度，规定角速度为逆时针方向。xOby为轴承坐标系，在此坐标系下的x和y表示转子中心Oj的横纵坐标。Op为轴瓦支点。ζiOpηi为第i块轴瓦的轴瓦坐标系。

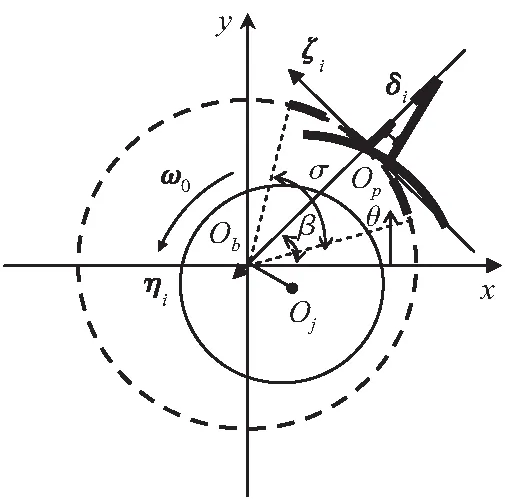
图1 可倾瓦轴承几何模型

2 转子振动主动控制的理论分析

2.1 雷诺方程及边界条件

假定轴承处于不可压缩、层流的状态下，其雷诺方程无量纲形式为：

(1)

运算中采用雷诺边界条件，即在油膜起始边界和破裂边界上满足下式：

(2)

2.2 油膜厚度

柔性铰链可倾瓦轴承在运转过程中，无量纲油膜厚度表达式[6,8]如下：

(3)

2.3 轴瓦的建模

2.3.1 轴瓦的受力分析

第i块轴瓦在转子运转过程中会受到油膜力的作用，可将油膜力分解为作用在铰链上的力Fiξ1与力矩与Ti1。为主动控制转子因不平衡载荷引起的振动，需在轴瓦的瓦背上施加通过轴瓦中心、与坐标轴夹角分别为αi1和αi2的力Fi1和Fi2。它们也可转化为铰链上的力与力矩Fiζ2和Ti2。主动控制力可由压电陶瓷装置提供，本文仅对控制力进行了理论计算，不对其实现方式进行过多论述。两部分力与力矩叠加为Fiζ和Ti，如图2所示。由油膜力产生的铰链上的力与力矩Fiζ1和Ti1的计算公式如下：

图2 轴瓦受力分析

(4)

(5)

由施加力Fi1和Fi2产生的力与力矩Fiζ2和Ti2的计算公式如下：

(6)

式中，αi1≠αi2。

铰链上两个力与力矩分别叠加的公式为：

(7)

2.3.2 轴瓦的运动方程

力与力矩Fiζ和Ti会作用于铰链使轴瓦分别产生相应的摆角δi1和δi2，计算公式如式(8)，式(9)所示：

(8)

(9)

其中，M′为轴瓦铰链系统的等效质量，J为轴瓦铰链系统的转动惯量，Cθ,Kθ为图2中ζi方向的阻尼和刚度，Cδ,Kδ为旋转方向的阻尼和刚度。Xiζ为轴瓦支点在ζi方向上的位移，可由此算出弯曲力Fiζ作用下产生的摆角δi1。

根据计算得出这些参数后，运用变步长的四阶五级Runge-Kutta-Felhberg算法[11]即可得出轴瓦在一段时间内的摆动规律。

2.3.3 摆角的合成

由公式(6)～公式(9)可得出轴瓦分别在弯曲力Fiζ和扭转力矩Ti作用下产生的摆角δi1和δi2，两部分相加即为轴瓦摆动的角度:

δi=δi1+δi2

(10)

2.4 转子运动方程

图3为转子在运转过程中的受力分析。由图可知，Fx和Fy为轴承非线性油膜力在x和y方向上的分力，可由公式(11)求得，Og为转子质量中心，eg为质量偏心距。

(11)

图3 转子受力分析

Qx和Qy为转子不平衡载荷引起的力在x和y方向上的分力，由公式(12)得出：

(12)

Mg为转子自身的重力，图3中箭头所指方向为正，相反为负，通过受力分析，得到转子的运动方程：

(13)

结合公式(12)、公式(13)，运用欧拉方法[10]即可得出转子在下一时刻的轴心位置及速度，如公式(14)所示。

(14)

即可求出一段时间内转子的轴心轨迹，由于Δt为无限小，且每段时间Δt内均需计算系统的非线性油膜力，因此所得出的轨迹为非线性轴心轨迹。

3 转子不平衡响应的主动控制

本文用到的柔性铰链可倾瓦轴承具体参数如表1所示：

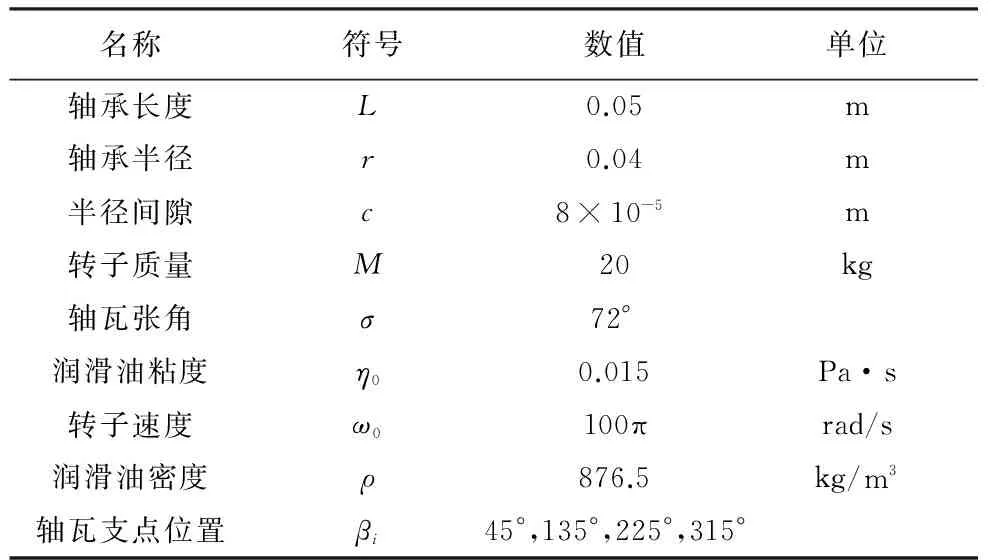
表1 轴承计算参数

时间间隔Δt=5×10-5s，平均雷诺数Re=58.74，转子质量偏心距eg取为 1.6×10-5m。

根据表1所列参数，即可得出转子的非线性轴心轨迹，具体步骤如下：

①确定轴承的计算参数；

②设定轴心的初始位置x、y以及四个轴瓦的初始摆角δi，计算此时转子的油膜厚度及非线性油膜力，并对转子进行受力分析；

③求得轴心在Δt时间后的下一位置；

④求解轴心所在位置每块轴瓦上的油膜厚度、非线性油膜力。对第i块轴瓦的瓦背施加力Fi1和Fi2，进而运用公式(4)～公式(7)求得每块轴瓦铰链上所受的力与力矩Fiζ和Ti；

⑤结合公式(8)、公式(9)，运用变步长四阶五级RKF法求得同一时间间隔Δt后每块轴瓦的摆角；

⑥重复步骤③～⑤直至x、y、δi的数值稳定为止。

3.1 不平衡载荷作用下轴承转子系统轴心轨迹的计算仿真

运用上述方法得出了轴承转子系统在轴瓦的瓦背施加力Fi1和Fi2为零，转子仅受重力和不平衡载荷作用时的非线性轴心轨迹和轴瓦摆角规律，如图4和图5所示。

图4 转子在不平衡载荷作用下的轴心轨迹

图5 四个轴瓦的摆动规律

由图4和图5分析知，不在轴瓦的瓦背上施加力，转子只受到重力和不平衡载荷的作用时，运转平稳后的轴心非线性位移、轴瓦摆角都随时间而周期变化，轴心轨迹近似椭圆。而由于摆角随时间周期性变化，因此柔性铰链上所受的力Fiζ和力矩Ti也随时间周期性变化。转子因不平衡载荷存在周期性的振动。分析知转子的周期性振动随不平衡载荷与转速的增大而增大，因篇幅有限不再做过多论证。

3.2 转子振动在一个方向上的主动控制

在t=0.1时刻对轴瓦四施加力F41和F42，取其与坐标轴的夹角α41和α42分别为15°和25°。由公式(6)、公式(7)通过合成到铰链上的力与力矩F4ζ2和T42控制F4ζ和T4，使周期性力与力矩F4ζ和T4频率不变，幅值变为原来的2倍，则施加力F41和F42的大小、转子在x和y方向上的非线性位移和施加力前后的轴心轨迹如图6～图8所示。

图6 主动控制力F41和F42随时间变化

图7 主动控制前后转子中心非线性位移

图8 主动控制前后的轴心轨迹

由图6～图8分析知，在瓦背施加力后，轴心轨迹经过一段较短时间的变化调整，由原先的轨迹稳定到新的轨迹。轴心轨迹主要沿着某一个方向进行变化，假定其与竖直方向的夹角为φ，而在与这一方向垂直的方向上变化不明显，在与竖直方向夹角为φ的方向上转子振动的主动控制效果比较明显。

3.3 转子振动在两个方向上的主动控制

在t=0.1时刻对轴瓦三的瓦背施加力F31和F32，对轴瓦四的瓦背施加力F41和F42，假定夹角均为15°和25°，使周期性力与力矩F3ζ和T3、F4ζ和T4频率不变，幅值变为原来的5倍，即施加力更大。则施加力F31和F32、F41和F42的大小、转子在x和y方向上的非线性位移和施加力前后的轴心轨迹如图9～图12所示。

图9 主动控制力F31和F32随时间变化

图10 主动控制力F41和F42随时间变化

图11 主动控制前后转子中心非线性位移

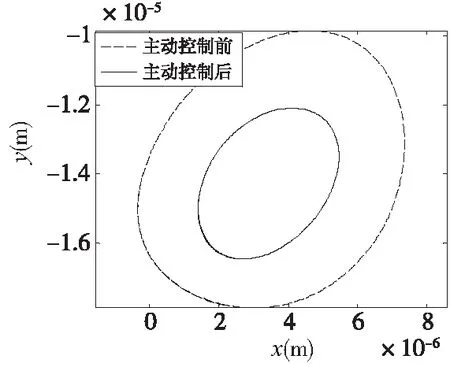
图12 主动控制前后的轴心轨迹

由图9～图12可知，对轴瓦三和轴瓦四同时施加力，经过较长的调整时间后，轴心轨迹由原来的稳定位置变为新的位置，在与竖直方向夹角为φ的方向和与它垂直的方向上，转子振动的幅值均减小，在两个方向上转子振动的主动控制均有明显的效果。

4 结论

(1)提出了一种新的转子振动主动控制的方法，通过对瓦背施加力，增大轴瓦铰链上力与力矩的幅值，抵消不平衡载荷的影响，进而使转子的振动减弱。

(2)分析了控制轴瓦与转子振动减小的方向性问题，控制一个轴瓦，可以使转子在某一方向上振动的幅值减小，而对与其垂直的方向无影响。若使转子振动在相互垂直的两个方向上均减小，至少需要对两个轴瓦进行主动控制。

[1] 张直明，张言羊，谢友柏，等. 滑动轴承的流体动力润滑理论[M].北京：高等教育出版社，1986.

[2] 刘思涌，肖忠会，闫志勇,等. 支点弹性、阻尼可倾瓦轴承动力特性数值仿真及实验研究[J]. 机械工程学报，2014，50(19)：88-97.

[3] 黑棣，吕延军，张永芳，等. 固定-可倾瓦轴承支撑的转子的非线性动力学特性[J]. 机械强度，2016，5(7)：79-87.

[4] Amira Amamou, Mnaouar Chouchane. Nonlinear stability analysis of long hydrodynamic journal bearings using numerical continuation[J]. Mechanism and Machine Theory ,2014,72(1):17-24.

[5] Kai F, Wanhui L,Z Zhang, et al. Theoretical model of flexure pivot tilting pad gas bearings with metal mesh dampers in parallel[J]. Tribology Intemational, 2016, 94: 26-38.

[6] Kyuho S, Daejong K. Design of flexure pivot tilting pads gas bearings for high-speed oil-free microturbomachinery[J]. Journal of Tribology, 2007,129:112-120.

[7] P Li, Y Zhu, Y Zhang, et al. The investigation of the temperature of high speed and heavy haul tilting pad journal bearing[J]. Industrial Lubrication and Tribology, 2015, 67(4):301-307.

[8] David A W Barton. Control-based continuation: Bifurcation and stability analysis for physical experiments[J]. Mechanical Systems and Signal Processing, 2015,3:77-90.

[9] Pixiang Lan, Jacob L. Meyer, Bita Vaezian,et al. Advanced polymeric coatings for tilting pad bearings with application in the oil and gas industry[J]. Wear, 2016, 4:56-65.

[10] 马金奎. 滑动轴承非线性轴心轨迹的瞬态与周期特性研究[D]. 济南：山东大学，2010.

[11] 宫晓春. 可倾瓦轴承-转子系统的非线性动力学分析与主动控制[D]. 哈尔滨：哈尔滨工业大学，2011.

[12] Lihua Y , Yanhua S, Lie Y. Active control of unbalance response of rotor systems supported by tilting-pad gas bearings[J]. Engineering Tribology,2012,226(2):87-99.

[13] 许太强，马金奎，路长厚，等. 瞬变载荷作用下滑动轴承动特性分析[J]. 润滑与密封，2013，38(4)：32-35,62.

[14] 薛定宇，陈阳泉. 高等应用数学问题的MATLAB求解[M]. 北京：清华大学出版社，2004.

(编辑 李秀敏)

Active Control of Rotor Unbalance Response Supported by Flexure-pivot Tilting Pad Journal Bearings

CHANG Jiang, MA Jin-kui，LU Chang-hou，CHEN Shu-jiang

(Key Laboratory of High-efficiency and Clean Mechanical Manufacture, Ministry of Education, School of Mechanical Engineering, Shandong Univercity, Jinan 250061,China)

Active control is used in rotor-bearing system in order to improve rotating accurcy. Based on the flexure-pivot tilting pad journal bearings, the computational model of axis center orbit and vibration rules of pads are built. Considering inertia of system as well as nonlinear film force, the axis center orbit and the vibration rules of pads are obtained when the rotor is affected by unbalanced response. And a new method about active control is put forword.The result shows that the rotor affected by unbalance load will vibrate periodically. Through exerting force on the back of a pad, the vibration rules of pads will be controlled and unbalanced load of the rotor will be offset. Then, vibration of the rotor decreases significently through active control, which greatly improves the rotating accurcy of rotor.

flexure-pivot tilting pad bearings；unbalanced response；vibration rules of pads；axis center orbit

1001-2265(2017)06-0097-04

10.13462/j.cnki.mmtamt.2017.06.025

2016-10-11；

2016-11-07

国家自然科学基金资助项目(51575318)

常江(1991—)，男，南京人，山东大学硕士研究生，研究方向为滑动轴承结构设计与主动控制，(E-mail)15564115362@163.com；通讯作者：马金奎(1962—)，男，山东聊城人，山东大学副教授、博士，研究方向为滑动轴承与转台，(E-mail)mjk@sdu.edu.cn。

TH133.3；TG506

A