一类带Gilpin-Ayala增长率的时滞计算机病毒模型
施键兰, 余赞平
(1.福建农林大学 东方学院, 福建 福州 350017; 2.福建师范大学 数学与计算机科学学院, 福建 福州 350117)
一类带Gilpin-Ayala增长率的时滞计算机病毒模型
施键兰1, 余赞平2
(1.福建农林大学 东方学院, 福建 福州 350017; 2.福建师范大学 数学与计算机科学学院, 福建 福州 350117)
研究了一类带Gilpin-Ayala增长率的时滞计算机网络病毒传播模型。通过分析模型特征方程及考虑时滞对系统动力学行为的影响,得到模型的平衡点稳定及 Hopf 分岔产生的条件。数值模拟验证出所得理论分析结果的正确性。
计算机病毒; Gilpin-Ayala增长率; 稳定性; Hopf分岔;时滞
计算机病毒的自我复制及传播行为和种群中流行病传播十分相似。1990年初,Kephart等人第一次借助生物学领域已有的数学模型来对计算机病毒进行研究,提出经典的SIS病毒模型[1]。在此基础上,不少学者对计算机病毒传播模型加以改进并进行研究[2-8];Ren等[8]考虑了易感染节点数量符合logistic增长,讨论了平衡点的动力学性质。
对于(时滞)微分方程描述的连续系统,如果参数通过某一数值时平衡点的稳定性发生了改变,且在平衡点附近产生了周期轨,那么称这样的分岔为连续系统的Hopf分岔。由于Gilpin-Ayala增长率比logistic增长率更加符合实际中的种群增长情形[9],本研究在文献[8]基础上,提出了一种带Gilpin-Ayala增长率的时滞计算机网络病毒传播模型,通过分析相应特征方程根的分布对其进行稳定性和Hopf分岔分析。
1 模型建立
假设将网络中一台计算机主机或路由器看作一个节点。节点分为易感染节点、感染节点和免疫节点。以S(t)表示t时刻未感染病毒的易感染节点数;I(t)表示t时刻已感染病毒的感染节点数;R(t)表示t时刻对病毒具有免疫能力的免疫节点数。根据上述假设,建立如下SIR计算机病毒传播动力学模型:
其中,β表示易感染节点与感染节点的传染率系数,假设易感染节点数量符合Gilpin-Ayala增长,r是内禀增长率,K是网络最大容纳量,μ表示节点自然死亡系数,α表示节点的免疫状态返回到易感染状态的概率,τ表示病毒的潜伏期,即节点感染病毒到病毒发作的时间间隔。
由于系统前2个方程不含有R变量,故可考虑如下系统
(2)
2 稳定性分析

2.1 平凡零解的稳定性
(λ-r)(λ+α+μ)=0
解得λ1=r>0,λ2=-α-μ<0。

2.2 无病平衡点的稳定性
定理2 系统(2)的无病平衡点E0=(K,0)
(1)当R0<1时是局部渐近稳定的;
(2)当R0>1时是不稳定的。
证明 系统(2)在E0处的特征方程为
(3)
(3)式有一个负实根λ1=-2r<0和满足下式的根
(4)
(1)当R0<1,τ=0时,得到(4)式的根
λ=Kβ-α-μ<0。
当R0<1,τ>0时,假设(4)式的根为
λ=iϖ(ϖ>0),代入(4)式分离实虚部得到
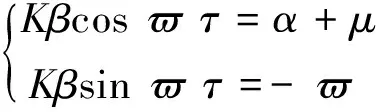
(5)
求解(5)式可得
(6)
当R0<1,方程(6)没有正根ϖ,这说明当τ≥0时(4)式F(λ)=0的所有根λ都具有负实部,所以系统(2)在无病平衡点E0是局部渐近稳定的。
(2)当R0>1时,(4)式F(0)<0,F(+)=+,所以F(λ)=0至少有一个正实根,系统(2)在无病平衡点E0是不稳定的。
2.3 地方病平衡点的稳定性
定理3 系统(2)的地方病平衡点
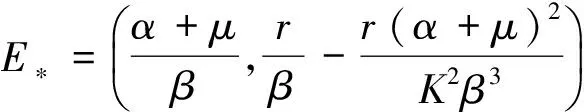
证明 系统(2)在E*处的特征方程为
(7)
这里c=α+μ。
当τ=0时,(7)式变为
(8)

由Hurwitz判据可得特征方程(8)的根的实部均为负,因此系统(2)当R0>1,τ=0时在地方病平衡点E*是局部渐近稳定的。
当τ>0时,假设(7)式的根为λ=iϖ(ϖ>0),代入(7)式分离实虚部得到
(8)
求解(8)式可得
(9)
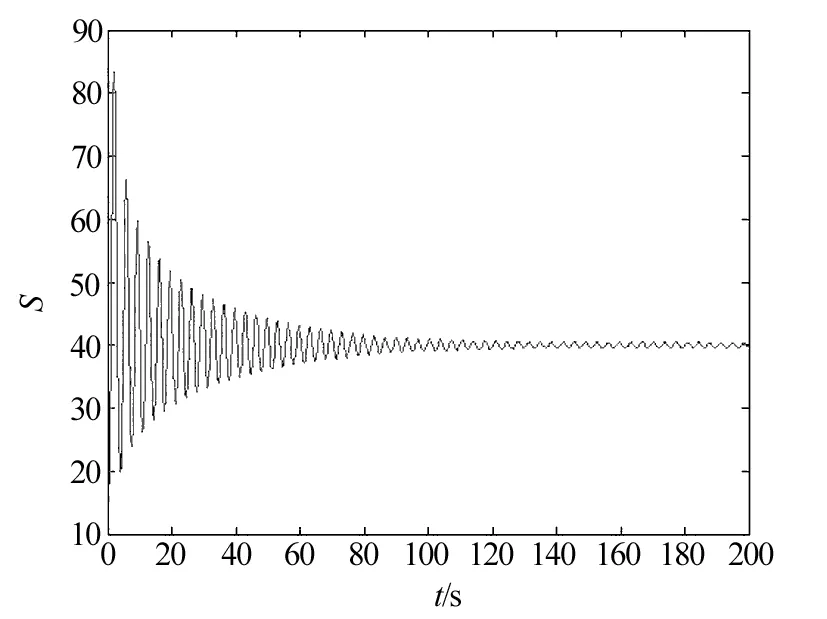
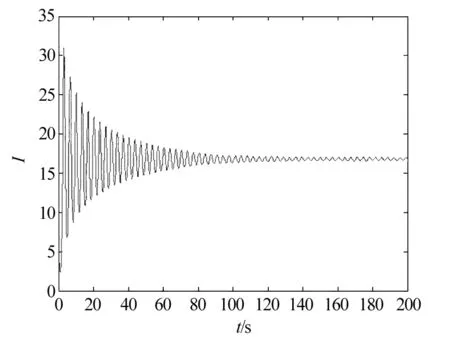
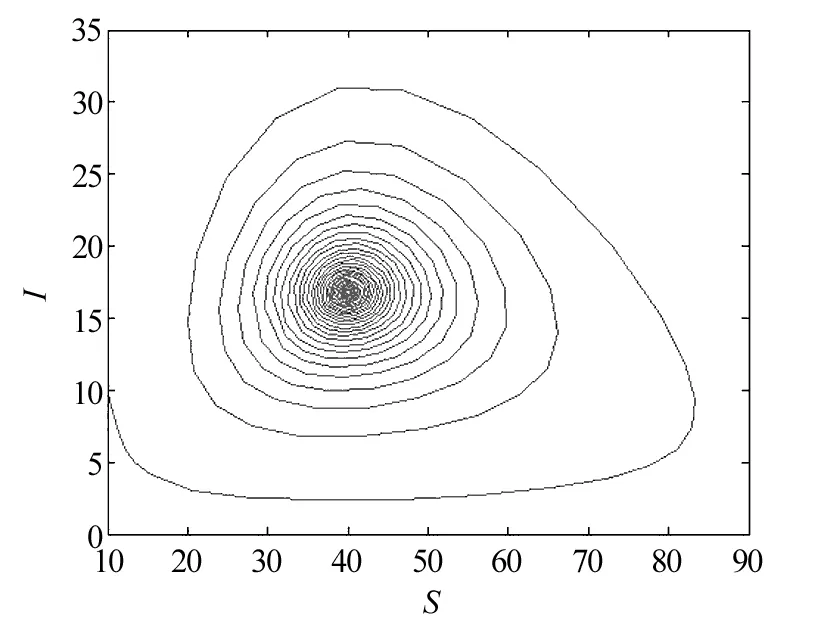
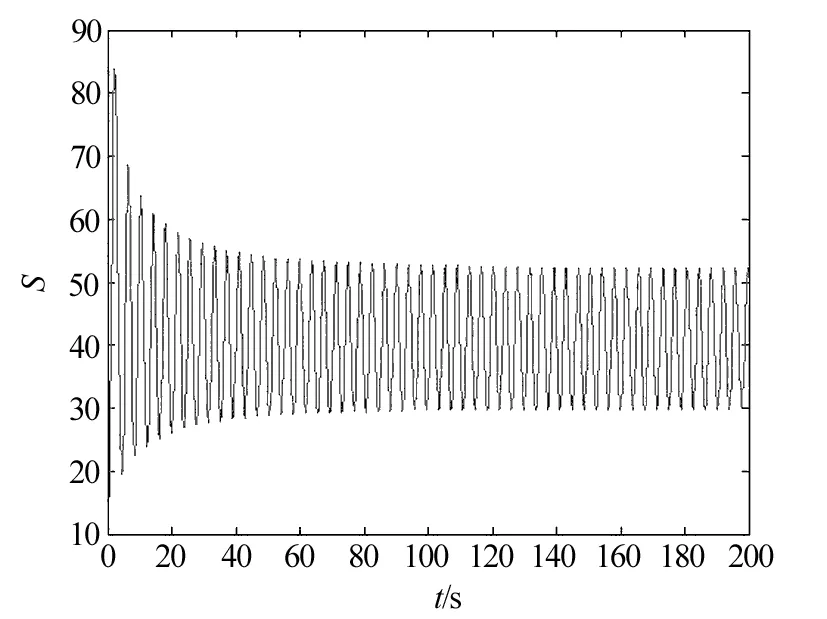
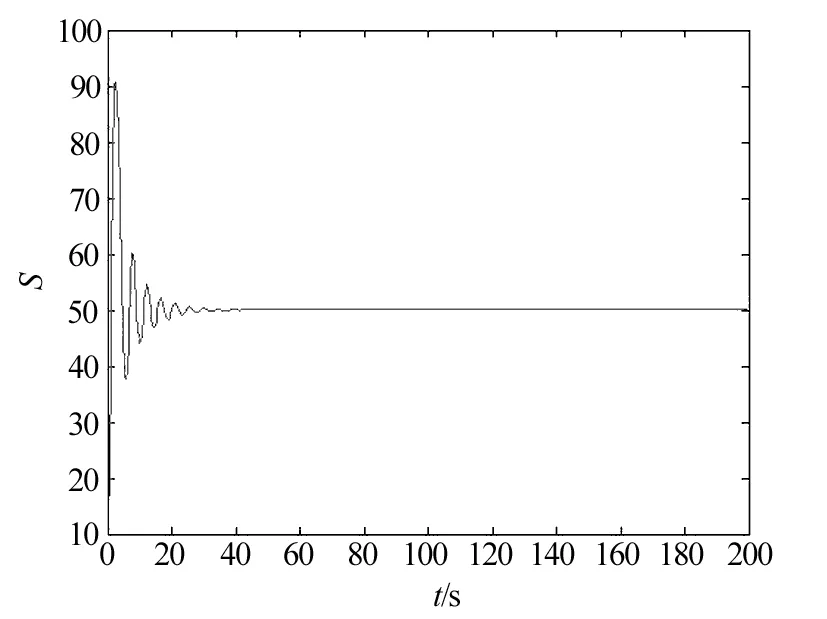
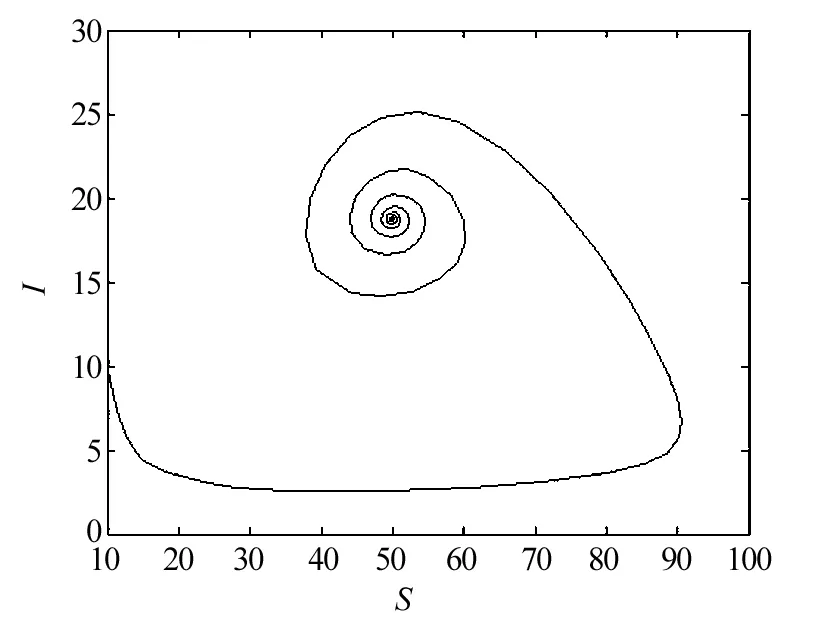
当1 定理4 当R0>5时,存在一个临界值τ0 (1)当τ∈[0,τ0)时,系统(2)的地方病平衡点E*是局部渐近稳定的。 (2)当τ>τ0时,系统(2)的地方病平衡点E*是不稳定的。并且当τ经过τ0时在地方病平衡点E*处产生Hopf分岔。 证明 当R0>5时,由(9)式解得 (10) 代入(8)式得 (11) 将特征方程(7)式左右两边对τ求导整理得 (12) 由(12)式得 (13) 根据(7)式计算得 (14) 将(14)代入(13)式得 (15) 所以 应用Hopf分岔定理[10],当R0>5,τ∈[0,τ0)时,特征方程(7)的所有特征根都具有复实部,系统(2)在地方病平衡点E*是局部渐近稳定的。当τ>τ0时,特征方程(7)至少有一个根具有正实部,系统(2)的地方病平衡点E*是不稳定的,并且当τ经过τ0时在地方病平衡点E*处产生Hopf分岔。 为了验证上述结果的正确性,对式(2)进行数值仿真如下: 取K=100,r=2,μ=2,α=2,β=0.1,计算R0和τ0得到R0=6.25>5,τ0=0.268 4,取τ=0.2<τ0,根据定理2,得到式(2)的解E*=(40,16.8)渐进稳定,如图1~3所示。 图1 R0=6.25>5,τ=0.2<τ0时,地方病不动点数值仿真t-S平面Fig.1 The t-S plane of endemic equilibrium when R0=6.25>5,τ=0.2<τ0 图2 R0=6.25>5,τ=0.2<τ0时,地方病不动点数值仿真t-I平面Fig.2 The t-I plane of endemic equilibrium when R0=6.25>5,τ=0.2<τ0 图3 R0=6.25>5,τ=0.2<τ0时,地方病不动点数值仿真S-I平面Fig.3 The S-I plane of endemic equilibrium when R0=6.25>5,τ=0.2<τ0 取K=100,r=2,μ=2,α=2,β=0.1,计算R0和τ0得到R0=6.25>5,τ0=0.268 4,取τ=0.3>τ0。根据定理3,得到式(2)的解E*=(40,16.8)是不稳定的,并且产生一个Hopf分岔,即分岔出一个周期解,如图4~6所示。 图4 R0=6.25>5,τ=0.3>τ0时,地方病不动点数值仿真t-S平面Fig.4 The t-S plane of endemic equilibrium when R0=6.25>5,τ=0.3>τ0 图5 R0=6.25>5,τ=0.3>τ0时,地方病不动点数值仿真t-I平面Fig.5 The t-I plane of endemic equilibrium when R0=6.25>5,τ=0.3>τ0 图6 R0=6.25>5,τ=0.3>τ0时,地方病不动点数值仿真S-I平面Fig.6 The S-I plane of endemic equilibrium when R0=6.25>5,τ=0.3>τ0 取K=100,r=2,μ=2,α=2,β=0.08,计算R0,得到R0=4<5,取τ=0.4。根据定理4,得到式(2)的解E*=(50,18.75)渐进稳定,如图7~9所示。 图7 R0=4<5,τ=0.4>τ0时,地方病不动点数值仿真t-S平面Fig.7 The t-S plane of endemic equilibrium when R0=4<5,τ=0.4>τ0 图8 R0=4<5,τ=0.4>τ0时,地方病不动点数值仿真t-I平面Fig.8 The t-I plane of endemic equilibrium when R0=4<5,τ=0.4>τ0 图9 R0=4<5,τ=0.4>τ0时,地方病不动点数值仿真S-I平面Fig.9 The S-I plane of endemic equilibrium when R0=4<5,τ=0.4>τ0 计算机病毒的防治是计算机安全领域的重要课题,是长期而复杂的任务,需要深入研究计算机病毒传播原理,对计算机病毒的有效预防和控制提供理论基础。本文提出了一种带Gilpin-Ayala增长率的时滞计算机网络病毒传播模型,研究基本再生数R0和时滞τ对网络病毒传播模型的影响。研究表明,当R0<1时,无病平衡点E0是局部渐近稳定的;当1 [1] Kephart J O,White S R.Directed graph epidemiological model of computer viruses[C]∥Proceedings of the IEEE Symposium on Security and Privacy, May 20-23,1991, Oakland, California, USA. Washington D C: IEEE Computer Society,1991. [2] 盖绍婷,唐功友, 于浩.带有免疫的计算机病毒传播模型的稳定性[J].中国海洋大学学报(自然科学版),2013,43(10):110-114. [3] 杨茂斌,杨小帆,祝清意.具有分级感染率的4仓室计算机病毒传播模型[J].重庆大学学报,2012,35(12):112-119. [4] 张道祥, 李 迅.非连续免疫策略对计算机病毒SIR模型的影响[J].应用科学学报,2016,34(3):329-338. [5] 陈旭辉,李尘,柯铭.一类具有个体差异性和非近邻传播特性的SIRS计算机病毒传播模型[J].计算机应用与软件,2013,30(5):15-19. [6] 胡宝安,李兵,李亚玲.具有时滞的SIR计算机病毒传播模型[J].计算机工程,2016,42(5):168-172. [7] 李君.具有密度依赖和有限抗病毒能力的计算机病毒模型的前向与后向分支[J].中山大学学报(自然科学版),2016,55(1):35-38. [8] Ren J, Yang X, Zhu Q. A novel computer virus model and its dynamics[J]. Nonlinear Analysis: Real World Applications,2012,13(1):376-384. [9] Fan M, Wang K. Periodic solutions of a generalized n-species Gilpin-Ayala competition model[J]. Computers and Mathematics with Applications,2000,40(10):1141-1151. [10] Hale J K, Verduyn L S. Introduction to Functional Differential equations[M].New York:Springer-Verlag,1993. (特约编辑:黄家瑜) A time delayed computer virus model with Gilpin-Ayala growth rate Shi Jianlan1, Yu Zanping2 (1. Dongfang College, Fujian Agriculture and Forestry University, Fuzhou 350017, China; 2. College of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350117, China) In this paper,a time-delay viral infection model in computer networks with Gilpin-Ayala growth rate was investigated.By analysing the associated characteristic equation and the impact of the time delay on the dynamical behaviour of a system,the conditions of equilibrium stability and the production of Hopf bifurcation were obtained.Numerical simulations confirm the theoretical results. computer virus; Gilpin-Ayala growth rate; stability; Hopf bifurcation; time delay 10.3969/j.issn.1672-4348.2017.03.020 2017-03-30 施键兰(1984-),女,福建福州人,讲师,硕士,研究方向:计算机模型。 TP309.5 A 1672-4348(2017)03-0301-063 Hopf分岔分析
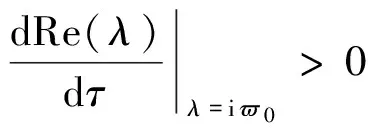
4 数值模拟



5 结语

