运算器中全加器标志位的逻辑设计与应用

汤龙梅， 陈敏， 许雪林

(福建工程学院 信息科学与工程学院， 福建 福州 350118)

运算器中全加器标志位的逻辑设计与应用

汤龙梅， 陈敏， 许雪林

(福建工程学院 信息科学与工程学院， 福建 福州 350118)

介绍全加器实现逻辑基础，给出4个常用标志位的生成逻辑，重点分析借位标志和溢出标志的生成逻辑，并给出标志位在MACH芯片中的实现过程。最后给出标志位在比较转移等指令中的应用方法。

计算机; 组成原理； 全加器； 标志位； 逻辑设计

运算器的核心部分是对数据信息进行加工处理的算术逻辑运算单元(arithmetic logic unit, ALU)，而ALU除了给出处理结果，还应给出结果的某些特征，如溢出否、有无进/借位输出等[1]。这些特征以状态标志位的形式提供，是CPU程序状态字的一部分。因此，运算器设计乃至CPU设计应包含标志位生成电路的设计。随着大规模集成电路制造技术的迅速发展，电子系统设计技术发生了很大的变化，将EDA和可编程逻辑器件设计与计算机组成原理授课相结合，让学生将理论应用于实践，已经在很多院校尝试[2-3]。多数计算机组成原理类教材详细介绍了ALU中全加器的设计原理[4-7]，但对标志位的生成逻辑并没有深入分析。文献[8-10]介绍了ALU处理逻辑的实现或优化方法，但没有给出除进位标志以外的标志位的实现过程。事实上，有些标志位如借位标志和溢出标志的生成逻辑并不像其概念那么直接。在全加器/全减器设计基础上，介绍了4个常用标志位的生成逻辑，重点分析了借位标志和溢出标志的生成逻辑，并给出了4个标志位在MACH芯片中的实现过程；最后给出了标志位在一些常用指令中的应用方法。

1 全加器/全减器的设计

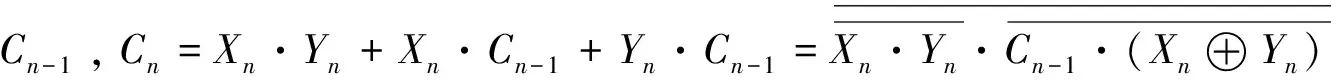
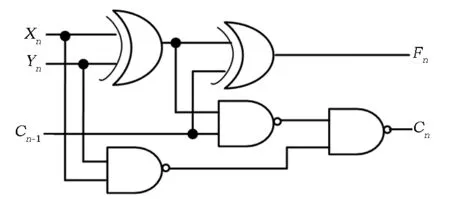
图1 1位全加器逻辑电路图Fig.1 Logic circuit of 1-bit full adder

由于定点数中的小数点并没有被编码成二进制位，因此，小数点对全加器而言是透明的。例如，二进制数0010b和1010b可表示十进制纯整数2和10，也可表示纯小数0.125和0.625(省略最左边的0.)，将这两个二进制数输入到4位全加器上进行相加：0010b+1010b=1100b。1100b既是12的二进制形式，也是0.75的二进制表示的小数部分(1100b左边补上0.即得0.75)，说明同一个全加器既可以实现无符号定点小数(小数点隐藏在最右边)相加，也可以实现无符号定点整数(小数点隐藏在最左边)相加，使用者自己明白小数点的位置即可。

对于有符号定点数，除了数值部分需要被编码，符号也需要被编码为二进制。常用的有符号数编码有原码、反码和补码等。由于采用补码表示时，中符号位可以与数值位一起参与运算，并且可以将减法转换为加法进行运算，因此计算机中一般均采用补码进行加减运算[4-7]。有符号定点小数与有符号定点整数的小数点对加法器而言，仍然是透明的。为避免重复，以下式子或示例均以定点整数为阐述对象。n位二进制整数补码(含1位符号位、n-1位数值位)加、减法公式分别见式(1)和式(2)[4-7]。

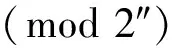
(1)

[x-y]补=[x]补+[-y]补(mod 2″)

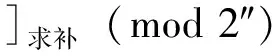
(2)

式(1)说明两个数和的补码等于各自补码相加后的和。在运算结果未超出范围时，对2n求模只需将进位直接舍弃即可得到。仍以上述0010b+1010b=1100b为例，这3个数可以分别是+2、-6和-4的4位补码表示，符合式(1)。当然如果当作定点小数处理，它们也可以是+0.25、-0.75和-0.5的4位补码表示(省略了最左边的0.)。

式(2)说明减法运算可转化成加上减数相反数的运算，式中[[y]补]求补是将[y]补连同符号位在内全部按位取反再加1。在全加器中增加一组非门将减数取反，并从最低进位位输入1，就可实现减法运算，因而不需另外设计减法器。Intel的74LS181和AMD的AM2901内部都是利用全加器和补码来实现减法运算的。

2 标志位生成逻辑分析

表征数据处理结果的特征很多，其中零标志ZF、符号标志SF、进/借位标志CF、溢出标志OF是最常用的4个标志位。下面依次对它们的生成逻辑进行分析。为便于描述，假设待运算数据为二进制数串X(X=XnXn-1…X2X1)和Y(Y=YnYn-1…Y2Y1)，运算结果为F(F=FnFn-1…F2F1)，低进位输入为C0，高进位输出为Cn。

2.1 零标志ZF

ZF标志是表征运算结果是否为零值。当FnFn-1…F2F1全为零时，ZF取值1，否则ZF取值0。可采用式(3)来实现。

(3)

2.2 符号标志SF

SF标志表征运算结果是正数还是负数，结果为正数时，SF取值0，否则SF取值1。有符号数运算与无符号数运算使用的是同一个加法器，区别只是把最高位看作符号位而不是数值位，因此SF直接取Fn即可。若Fn为1即SF为1，表示结果为负数，反之为非负数。

2.3 进/借位标志CF

CF标志用来表示加法运算是否产生进位，或减法运算是否产生借位，只对无符号数运算有意义。加法的进位标志取全加器的最高进位输出位Cn即可。串行进位加法的进位生成逻辑比较简单，此处主要讨论借位生成逻辑。

由于减法运算是借助加法来实现的，如果直接采用全加器的进位输出作为借位标志，则与借位定义正好相反。这一点在AM2901和74LS181上都可以得到体现，下面对此进行分析。

根据[[y]补]求补的运算规则，将[y]补按位取反等效于(2n-1)-[y]补，根据式(2)，可得：

[x-y]补= [x]补+ (2n-1) - [y]补+ 1=

[x]补- [y]补+ 2n.

由于此时的x和y都是无符号数，故：

若x≥y，则[x]补≥[y]补，故[x]补- [y]补+ 2n≥ 2n，因而产生进位；

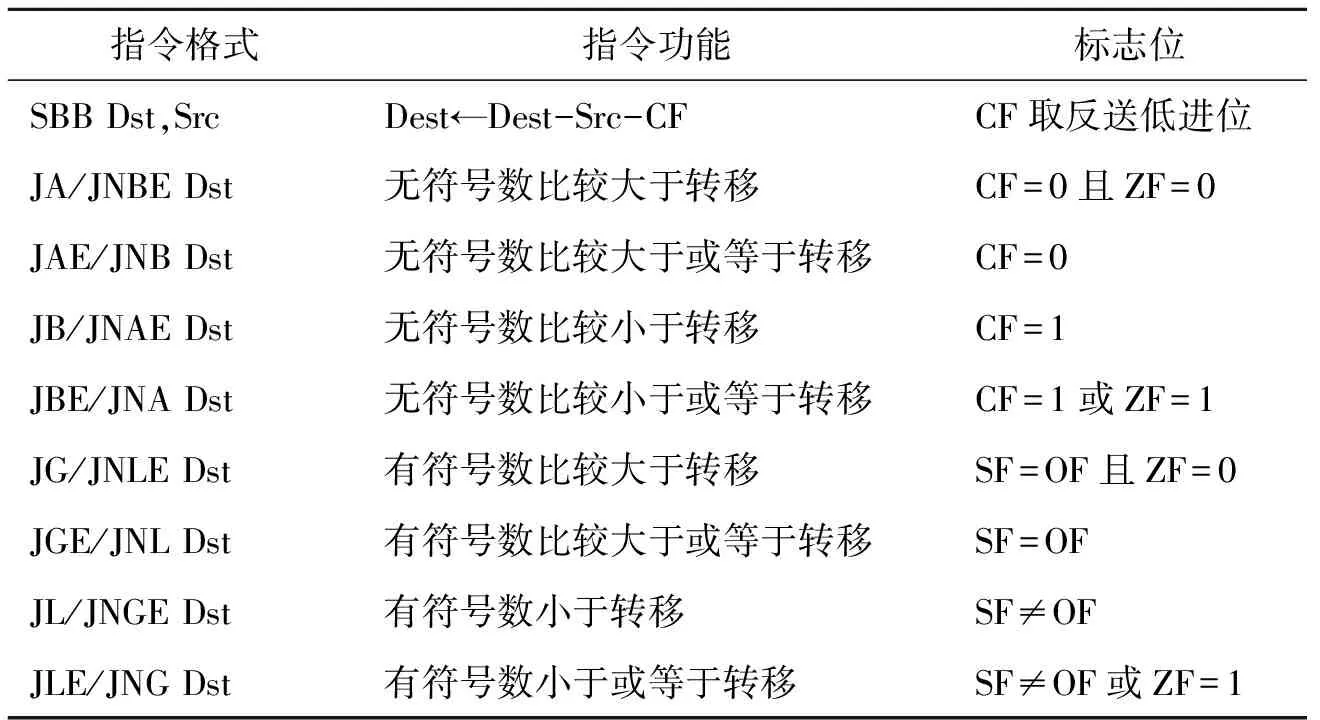
若x

分别以减法2-3=-1和3-2=1予以例证。为简便起见，补码采用4位二进制(下同)。运算器中2-3的运算过程是：2的补码0010b和3的补码0011b分别输入全加器，0011b按位取反得1100b，最低进位位送入1，最后三者相加：0010b+1100b+1 =1111b。1111b正好是-1的补码，说明运算结果正确，但Cn=0，与实际有借位刚好相反。

3-2的运算过程是：3的补码0011b和2的补码0010b送入全加器，0010b按位取反得1101b，最后0011b+1101b+1=10001。0001b正好是1的补码，但Cn=1，与实际无借位刚好相反。

根据上式分析，生成符合一般意义上的进/借位标志的生成逻辑见式(4)，其中ADD和SUB分别表示加法和减法运算。

(4)

文献[1]基于AM2901运算器芯片设计了16位运算器，将最高位AM2901的进位输出Cn+4直接作为CF，因此后续将CF用作借位标志时要作相应处理。

2.4 溢出标志OF

OF标志用于表示当两个有符号数进行加、减运算时，运算结果是否超出了范围。若超出，则OF取值1，否则取值0。常用的溢出判断方法有3种：双进位判断法、单符号位判断法和双符号位判断法[11]。这些方法在某些场合并不完全等价，但相关文献并未给出它们的区别。下面予以对比分析。

2.4.1 双进位判断法

将最高进位Cn与次高进位Cn-1异或得到OF。双进位法对于加法溢出的判断没有问题，但对借助加法实现的减法溢出判断而言，直接将Cn⨁Cn-1作为OF输出是有局限性的。以4位二进制补码实现-1-(-8)=7和+1-(-8)=9为例，-1-(-8)的运算过程是：-1的补码1111b和-8的补码1000b送入运算器，1000b按位取反得0111b，低进位位送入1，最后1111b+0111b+1 =10111b。0111b正好为+7的补码，而次高进位为0，最高进位为1，故OF=1，与实际无溢出相反。类似的，可得到+1-(-8)的运算结果为1001b，为-7的补码，显然结果溢出了，但此时OF却为0。

之所以出现上述情况仍然是由于对第二操作数取反导致的。4位二进制补码数的范围为[-8,+7]，-8的相反数为+8，已经超出范围了。上例中减去(-8)运算实际变为加上(-8)的运算，导致最后溢出标志出错。因此，当减数为-2n-1时，需对原溢出标志取反，增加了处理电路的复杂性，见式(5)。

(5)

2.4.2 单符号判断法

若两操作数的符号相同，而结果符号与操作数符号相反，表示结果超出范围。可以理解为正数与正数相加，结果得负数；或负数与负数相加，结果得正数。这两种情况都是不可能的，故出现了溢出。

对减法运算溢出判断可以描述为：若两操作数符号相异，而结果符号与减数符号相同(与被减数符号相反)，则溢出。可以理解为正数减负数，结果为负数；或负数减正数，结果为正数。这两种情况也都是不可能的。

综合两种情况，OF的生成逻辑见式(6)。

(6)

该方法依据取反前的数据符号以及结果符号进行判断，对第二操作数取反后是否溢出不影响最终的OF，因此不会出现方式(1)中的特殊情况，但仍然比较复杂。

2.4.3 双符号判断法

操作数和运算结果均采用双符号，如果运算结果的两个符号位相异，则说明出现了溢出，因此只需将双符号进行异或即可生成OF。如上例，-1-(-8)的运算过程是：-1的补码11111b和-8的补码11000b送入运算器，11000b按位取反得00111b，最后执行：11111b+00111b+1=100111b，双符号位为00，故没有溢出。而1-(-8)的运算过程为：00001b + 00111b+1=01001，结果溢出，此时双符号位01中的0表示实际的符号，1是结果的最高数据位，因而正确的结果是+9。

在本方法中，全加器需要额外增加一位，即n位二进制补码数相加减需要n+1位全加器。虽然增加了硬件开销，但简化了OF的生成逻辑，且容易获取正确的运算结果。要注意的是，双符号由ALU内部产生用于溢出判断，对用户来说是透明的，其他标志位仍按原有逻辑。

3 标志位的实现

笔者用计算机组成原理实验箱TEC-2000A上的iM4A5-128/64芯片作为可编程逻辑器件，采用LATTICE公司的ispLEVEL开发环境和ABEL语言，设计了一个包含4个标志位的4位全加器。利用实验板上的拨动开关输入X1～X4和Y1～Y4、低进位C0以及运算功能选择M(输入0给M表示做加法，输入1给M表示做减法)，将运算结果F1～F5和各状态位送往LED指示灯进行显示，测试结果符合上述分析。主要语句如下：

EQUATIONS

//5-bit串行进位ALU,M=0加法，M=1减法

F1 = X1 $ (Y1$M) $ C0;

C1 =(X1&(Y1$M)) # (X1&C0) # ((Y1$M)&C0);

F2 = X2 $ (Y2$M) $ C1;

C2 =(X2&(Y2$M)) # (X2&C1) # ((Y2$M)&C1);

F3 = X3 $ (Y3$M) $ C2;

C3 =(X3&(Y3$M)) # (X3&C2) # ((Y3$M)&C2);

F4 = X4 $ (Y4$M) $ C3;

C4 =(X4&(Y4$M)) # (X4&C3) # ((Y4$M)&C3);

F5 = X4 $ (Y4$M) $ C4; //双符号位高位，把X4和Y4当成X5和Y5;

C5 =(X4&(Y4$M)) # (X4&C4) # ((Y4$M)&C4);

ZF = !(F1#F2#F3#F4); //零标志

SF = F4; //符号标志

CF =(!M &C4) # (M&!C4); //进位/借位标志

//OF1～OF3均为溢出标志

OF1 = (!M&(C4$C3))

#(M&((Y==[1,0,0,0])$(C4$C3)));

OF2 = !M&(X4&Y4&!F4 # !X4&!Y4&F4)

#M&(X4&!Y4&!F4 # !X4&Y4&F4);

OF3 = F5$F4。

在上述代码中，$、#、&和!分别是异或、或、与和非这4种常见逻辑运算。为对比不同溢出标志生产方式，此处实现了双符号位运算，因此，4位二进制的加减运算需要5位全加器，F1～F4为相加或相减后对应的和或差的输出。ZF为零标志，从它的逻辑表达式可以看出，只有当F1～F4全为0，ZF才会输出1。SF为运算结果的符号位，直接取自F4。CF为加法进位输出或者减法的借位输出，当执行减法操作时，需要对C4取反才是正确的借位标志值。OF1、OF2、OF3分别是双进位溢出判断法、单符号溢出判断法和双符号溢出判断法。从逻辑表达式上看，OF3表达式最简单。

4 标志位的应用

用户通过计算机指令来获取或使用标志位所代表的含义，而指令的执行要依靠CPU，因此CPU设计者需要根据指令功能正确选择标志位来控制指令的执行。与标志位相关的指令数目众多，此处选取了Intel8086汇编指令系统中比较容易混淆的带进位减法和比较转移类指令[12]来分析如何应用上述4个标志位控制指令的执行，表1是这些指令应用标志位情况的汇总说明。当然，本研究的控制方法是实验性的，与Intel8086CPU的实现方法没有直接关联。

表1 常用转移指令标志位取值要求

4.1 带借位减法指令SBB Dest,Src

该指令的功能是Dest←Dest-Src-CF，CF为当前借位标志值。不带借位减法运算由ALU内部将减数取反、低进位位补1后再执行全加运算。若低进位补0，则相当于CF为时的带借位减法操作；而若低进位补1，则相当于CF为0时的带借位减法操作。故CPU在控制SBB指令执行时，需将借位标志CF取反，再送往全加器最低进位。

4.2 无符号数比较判断指令

根据指令功能，无符号比较的4类指令可以分为条件正好相反的两组：JA/JNBE与JNA/JBE为一组，JB/JNAE与 JNB/JA为一组，因此，确定组内一方的判断条件后，另一方判断条件只需将对方条件取反即可。

若CF=1，表示两数相减产生了借位，说明被减数小于减数，对应JB和JNAE的转移条件。反之，若CF=0，表示没有借位，说明被减数不小于减数，对应JNB/JAE的转移条件。

若CF=0且ZF=0，说明被减数不小于减数且两数之差非零，故符合JA/JNBE的判断要求。反之，若CF=1或ZF=1即为JNA/JBE的判断要求。

根据指令含义，也有将JAE指令的判断条件设为CF=0或ZF=1，将JB的判断条件设为CF=1且ZF=0。实际上，满足ZF=1的情形是满足CF=0情形的子集，相应的若CF=1，则ZF不可能为1。因此这两条指令的判断条件只需根据CF的取值即可。

要注意的是，由于无符号数中的最高位是数值位而不是符号位，故符号标志SF不宜用于无符号比较转移指令的转移判断依据。例如1100b和0000b(分别对应无符号十进制数12与0)相减后得1100b，这种情形下SF=1，CF=0。很明显，CF=0表示12减1不需借位，故能正确判断两数谁大谁小。若根据SF=1判断差为负数，进而说明不够减，显然是错误的。

4.3 有符号数比较判断指令

对于有符号数比较，需分溢出和不溢出两情况。若没有溢出，则SF为正确的结果符号；若有溢出，虽然运算结果不正确，但大小关系仍然可以判断。此时，SF取值与实际符号正好相反。与无符号数比较指令分组类似，指令JG/JNLE和JNG/JLE是一组，指令JL/JNGE和JNL/JGE是另一组。

若OF=0且SF=0，或者OF=1且SF=1，都表示被减数不小于减数，即SF=OF对应指令JNL和JGE的转移条件。相应的OF≠SF对应指令JL和JNGE的转移条件。

若OF=0且SF=0且ZF=0，或者OF=1且SF=1且ZF=0。表示被减数大于减数，即SF=OF且ZF=0对应JG和JNLE的转移条件。相应的OF≠SF或ZF=1对应JNG和JNLE的转移条件。

5 结论

标志位与运算器、指令系统、CPU以及汇编程序设计关系密切。

通过对常用标志位ZF、SF、CF和OF生成逻辑的分析、实现及应用的详细阐述，可以更好地了解运算器的工作原理及设计方法，进一步理解运算器、指令系统以及控制器3者之间的联系，提高汇编程序设计能力。

[1] 王诚,宋佳兴.计算机组成与结构[M].2版.北京:清华大学出版社,2011.

[2] 秦磊华,王小兰,管军.EDA仿真在组成原理设计性实验中的应用[J].实验室研究与探索,2009,28(4):79-82.

[3] 张磊，郑榕，张军峰.计算机组成原理理论实验教学无缝结合的新方法[J].实验室研究与探索,2013,32(5):168-171.

[4] 白中英.计算机组成与系统结构：第五版(立体化教材)[M].北京:科学出版社,2011.

[5] 裘雪红,李伯成.计算机组成与体系结构[M].北京:高等教育出版社,2009.

[6] 唐朔飞.计算机组成原理[M].2版. 北京:高等教育出版社,2010.

[7] 王爱英.计算机组成与结构[M].5版. 北京:清华大学出版社,2013.

[8] 袁波,李树荣,姚素英.一种8位单片机中ALU 的改进设计[J].微电子学与计算机,2006,23(4):71-74.

[9] 朱一杰,张曦,俞军.算术逻辑单元的优化设计[J].微电子学与计算机,2004,21(9):155-157.

[10] 宋文强.12位RISC计算器设计[D].成都：电子科技大学,2011.

[11] 齐广玉,邹建伟.计算机组成原理[M].北京:兵器工业出版社,1997.

[12] 沈美明.IBM PC汇编语程序设计[M].北京:清华大学出版社,1996.

(特约编辑：黄家瑜)

Logical design and application of flags for ALU’s full-adder

Tang Longmei, Chen Min, Xu Xuelin

(College of Information Science and Engineering, Fujian University of Technology, Fuzhou 350118, China)

The logical basis of the implementation of full-adder was described. The generation logic of 4 commonly used flags was presented based on the circuit logic of the full-adder. The generation logic of carrying flag and overflow flag were analysed. Then the implementation of the flags in a MACH chip was focused. Finally, the application of the flags in some instructions such as transfer instruction was discussed.

computer; composition principle; full-adder; flag; logical design

10.3969/j.issn.1672-4348.2017.03.018

2017-01-07；

2017-03-25

福建省教育科学“十二五”规划课题(FJJKCG15-180)

汤龙梅(1977-)，女，江西永新人，讲师，硕士，研究方向：嵌入式技术、机器学习。

TP303; G642

A

1672-4348(2017)03-0289-05